メールマガジン宝箱 Mail magazine

　今回の組分けテストでは、「立体の切断」や「平面図形の移動」といった難問を多く含む単元を通して、自分で作図をし、図にかき込みをすることで問題内容を正しく把握する力、そしてそこから解答方針を速く正確に立てる力が試されます。

　6年生最後の組分けテストをむかえ、問題の複雑さが増してくる中で、制限時間内に問題内容を的確にイメージすることが高得点をとるポイントになります。正確な作図を通して解答を進める力が求められる、第3回組分けで一気にクラスアップを実現したいところです。

　そこで、第3回組分けテストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの「50分で偏差値を5上げる算数予想問題」と組み合わせれば、組分けテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　立体の切断：切断の基本的なルールを完全習得できていますか？】

　「立体の切断」については、『予習シリーズ5年下第14回』で切断の基本的な成り立ちを学習しましたが、今回の組分けでは「2段階切断」などの応用編から出題されることになります。難問対策を進める上でも、切断の基本的なルールを改めて確認しておきましょう。

　まず大原則が「向かい合う平面に入る切断の線が平行になる」ことで、この原則にしたがえば、切断によってできる向かい合う図形の相似関係をスムーズに把握できます。図形（三角形）の相似関係さえつかめれば、主に大問の(1)で出される、切り口の面を立体の辺が交わる点の位置をスムーズに解答することができるようになります。

　そこからさらにレベルアップして覚えておきたいのが、立体を複数回切断するパターンの解法です。『予習シリーズ算数6年上』では第11回の117～119ページに掲載されている「複数回の切断」と「すい体の切断」の部分を熟読して、解法のポイントをしっかりおさえておきましょう。

　例えば下の図のように、立方体を3つの頂点を通る平面で切断してできる三角すいを、さらに新たな平面で切断するパターンがありますが、ここでも切断の重要ポイントである「平行関係」を正確に見つけ出すことが必須となります。

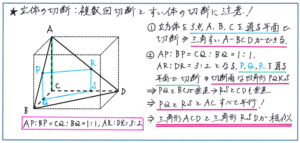
　切断面、切断線がどのように立体の中に入るかをつかめれば、あとは平行線に着目することで相似を利用した解法へとつなげることができます。相似の関係を使うことを念頭に置いて、切断の様子を注意深く確認するようにしましょう。

　また、切断の問題では、与えられた図形の中に線を書き入れて解き進める必要がありますが、複数回切断ではその線の本数が多くなりますので、見えづらくならないように、ていねいに線を引く練習を重ねておきましょう。

【第2位　食塩水の濃度：「濃さが等しくなる」場合の解き方を覚えていますか？】

　食塩水の濃度の中で、異なる濃度の食塩水を混ぜ合わせるタイプの問題はテストでも頻出です。こうした問題では、ビーカー図を使って混ぜ合わせのやりとりを正しく把握することが大事ですが、特に気をつけておきたいのが、「混ぜ合わせた結果、濃さが等しくなる」のパターンです。

　もとからある食塩水に、水も食塩も加えず、ただ互いにやりとりする場合には、「濃さが等しくなる」ことが問題を解く上で大きなヒントになりますので、見逃さないようにしましょう。

　例えば次のような問題はどのように解き進めればよいでしょうか。「容器Aには8%の食塩水が500ｇ、容器Bには12%の食塩水が300ｇ入っています。A、Bからそれぞれ等しい量の食塩水をくみ出し、Aからくみ出した分はBに、Bからくみ出した分はAに入れてよくかきまぜると、AとBの食塩水の濃さは等しくなりました。くみ出した食塩水の重さは何ｇずつですか。」

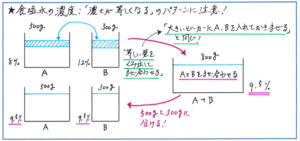
　食塩水の混ぜ合わせですので、面積図を使って解くことにはなりますが、くみ出した食塩水の量がわからないので、すぐには図をかき始められないところです。

　そこで、等しい量の食塩水をやりとりしたことに注目すると、Aの容器の食塩水は500ｇ、Bの容器の食塩水は300ｇのままで変わらずに、食塩も水も新たに追加されていません。そのうえで2つの容器の濃さが等しくなるので、上の図のような、大きなビーカーにA、Bそれぞれの食塩水を入れてよくかきまぜて、それをAに500ｇ、Bに300ｇ戻したことと同じになります。

　大きなビーカーにある800ｇの食塩水の濃さは、それぞれの容器に含まれる食塩の量を出せば、図をかかなくとも計算のみで求められますが、練習にもなるので、面積図で解いてみましょう。

　大きなビーカーにある800ｇの食塩水の濃さは9.5%になりますので、ここからは容器Aのみに注目すると、問題の内容が、「8%の濃さの食塩水と12%の濃さの食塩水を混ぜ合わせて9.5%の食塩水500ｇになりました。12%の濃さの食塩水は何ｇですか。」と変わったことになります。ここからは面積図を使って、500×3/8＝187.5より答えは187.5ｇと求めることができます。

　濃さの混ぜ合わせは必ずビーカーでやりとりを示す、と決めつけず、まずは問題内容を的確に理解し、そこからより効率的に進められる解法を使いこなしましょう。

【第3位　図形の平行移動：図形の移動距離を正確に把握することができていますか？】

　今回の組分けテストの平面図形の範囲の中には、「図形の移動」という入試頻出の重要単元が含まれます。図形の動きを正確に把握したうえで、その動きと面積や長さの変化がどのように関係するかを導き出す力が試され、また、グラフと合わせて出題されるケースも多く、速さ、相似といった受験算数のエッセンスが盛り込まれた難問となるケースが多くあります。

　まずは図形の動きを正確に把握するために、図形のどの部分に着目するかを間違わないようにしましょう。具体的には、例えば下の図のように直角三角形が移動する場合、図形全体の移動としてとらえると移動距離を取り違えてしまうことがありますので、図形の中のある頂点の動きを追うようにして、長さの取り違えといったミスを防ぐようにしましょう。

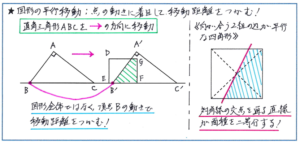
　また、もう1点確認しておきたい項目として、平行四辺形のように2組の辺が平行な関係にある四角形（正方形、長方形をもちろん含みます）の面積を二等分する直線が「対角線の交点を通る」ということに注意しておきましょう。図形の平行移動の問題でも、「直角三角形と正方形の重なった部分が正方形の面積の半分になるのは何秒後か」といったかたちで出題されることがあります。

　重なった部分ともとの図形の相似の関係は最頻出ですが、面積を二等分するケースにも注意しておくようにしましょう。

【第4位　円の転がり運動：回転する円の「向き」を正確に把握するためのかき込みができていますか？】

　今回の組分けテストの範囲となる「図形の移動」では、【第3位】で取り上げた「平行移動」以外にも、長方形のまわりや内部を正三角形や円が回転移動するパターンも重要な単元となります。

　こうした回転移動する問題では、辺（円やおうぎ形であれば半径・直径）の動きをとらえたうえで、回転の様子を図にすることが重要で、いずれも丁寧になり過ぎない範囲で、見やすく図をかく練習が不可欠となります。

　そんな中で特に注意しておきたいのが、下の図のような、円のまわりを円が転がって移動するタイプの問題です。特に回転数を求める問題は、頭の中だけで解こうとしても、イメージが非常に難しいケースになります。

　下の図のような、同じ半径の円どうしでも、『予習シリーズ算数6年上』のP.129「発展例題1」のような半径の長さが異なる場合でも、共通するのは「同じ長さの弧の部分」に着目することです。そこで、下の図のようにそれぞれの円周上に記号やアルファベットを記しておくと、同じ長さの弧の部分をより明確にとらえることができます。

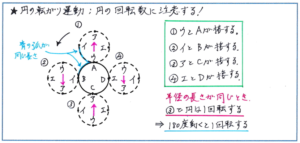
　回転数を求める問題では、『予習シリーズ』P.130～131に記載されている、「回転数＝中心が動いた長さ÷円周」の式でも求めることができますが、弧の長さから式を立てる解法を身につけておくと、初見の問題への対応力が大きくアップしますので、じっくりと解法の理解を進めておきましょう

【第5位　わり切れる回数：素因数分解を使う解法の流れを確実に使いこなせていますか？】

　「数と規則性」の単元からは、約数・倍数の問題、既約分数をはじめとした分数・小数の問題と幅広い問題が出題対象になります。作図などの手作業を必要とする図形の難問が多い今回の組分けテストにおいて、この単元での高い正答率が高得点の重要な下支えとなります。

　特に注意すべきは「素因数分解」を使った解き方をしっかりと覚え込むことにあります。

　例えば、約数の個数を求める問題では、約数を書き出すのではなく、素因数分解をした結果から計算で求める方法がスピーディーかつ正確に解き進めるために必須となります。6年生のテストともなると、約数の個数を求める問題で、その数が普段あまり接したことのないような値や、大きな数になることがあります。そうした場合に書き出しを使っていては過大な時間を費やしてしまいます。時間をできる限り短縮するためにも、「素因数分解→（素因数の数＋1）のかけ合わせ」、の解法がすぐに思い浮かぶようにしておきましょう。

　そして特に注意しておきたいのが「わり切れる回数」の問題です。書き出しという地道な解法が有効に使えないタイプの問題で、解法を確実に覚えていなければ、得点のチャンスが大きく減ってしまいます。逆に解法を使いこなせれば、確実な得点源にすることができます。

　下に紹介しました「1×2×3×…×80と、1から80までの整数を順にかけた積をNとしたとき、Nを3で割り続けると、何回目で商が整数でなくなりますか」といった問題。Nを素因数分解したときに、「3」を何個かけ合わせているか、つまり「3」の個数が何個あるかを調べるという流れを反復連習しておいてください。

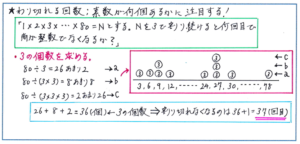
　今回の組分けテストでは、「数と規則性」の単元からの問題では、できる限り解答時間を短縮しておきたいところです。もちろん解法が浮かばない場合は書き出しの作業を進めればよいのですが、素因数分解などの強力ツールを使って、スピーディーに解答を進める対策を、しっかりと重ねておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。