メールマガジン宝箱 Mail magazine

　今回の組分けテストでは、「速さ」での運転間隔やグラフの問題、「平面図形」での相似、「場合の数」での最短経路など、自分で図をかく、または図やグラフにかき込みをするといった手作業を多く求める単元が出題範囲となります。ただ闇雲に作業を進めても、時間がかかり正答率も上がらないといった事態が起こりがちです。しっかり練習を重ねて、正確で効率的な作業を進める力が求められる組分けで、一気にクラスアップを実現したいところです。そこで、第2回組分けテストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！
　さらにこちらの算数予想問題と組み合わせれば、組分けテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　速さのグラフ：グラフの中に問題を解きやすくする情報をかき込めていますか？】

　速さの問題の中でもグラフを使って解く問題は、どれだけ必要な情報をグラフの中にかき込み、そこから式の立て方を考えられるかで、解答速度と正確さに大きな違いが生まれます。特に動きが複雑な問題では、グラフを通して解法のイメージを明確にする必要があります。その典型的な例が「往復運動」を含む問題です。ただ往復運動を表すグラフだけを読み取るだけであれば難しさは感じられませんが、そこに別の動きを表すグラフが混ざることで難度が大きく上がります。　
　例えば、下のグラフは駅と学校の間を往復するバスと、駅と学校の間にある家から駅に向って一定の速度で進む花子さんの動きを表しています。ここで、「花子さんが学校に向かうバスにはじめて追いこされてから、駅に向かうバスとはじめてすれ違うまでの時間」がグラフのどの部分にあたるかを、スピーディーに見つけ出す力が求められます。そこで、2つのグラフが交わる3点のうち、どの点が問題で求められているものに当たるのかを判断するために、バスと花子さんの進行方向を矢印でかき込むとよいでしょう。矢印の向きを参考にすることで、花子さんがバスにはじめて追いこされたのが点Ｐ、はじめてバスとすれ違ったのが点Ｑと見分けることができます。

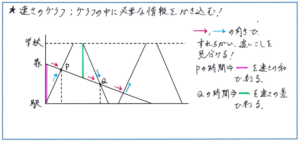
　グラフ上で求める点さえ把握できれば、時間を求めるために直前の両者の間の距離を求めて、旅人算の基本式で解くことができます。求めるものが時間ではなく距離に変わったとしても、計算内容を変えればよいだけですので、まずはグラフのどの部分を解答対象とするかを正確に求めるようにしましょう。グラフの問題に慣れていれば、こうした作業が無駄に思われるかもしれませんが、テスト会場で焦らず正確に解き進めるためには、ぜひグラフへのかき込み方法を身につけておきましょう。

【第2位　平面図形：2つの相似の関係を使いこなす問題に対応できていますか？】

　平面図形の問題では、比を答えさせるケースが非常に多くなってきます。そうした問題では、相似や面積比（同じ高さを持つ図形の面積比が辺の比になる）を利用しますが、注意しておきたいのが、下の図のような、1本の直線を3つの比で分けるパターンです。まずは、こうした問題を見た瞬間に「2つの相似の関係を使う」とすぐに思い浮かべることができるようにしておきたいです。解答方針が立てられれば、後は、図形の中に相似の関係を見つけられるように、見る向きを変えて図形を注視します。そして、辺の長さの比を求める際に、下の図であれば、ＡＧ：ＣＧ＝1：2としないように気をつけましょう。三角形ＡＥＧと三角形ＣＤＧの相似比は、ＡＥ：ＣＧ＝1：(1＋2)＝1：3となります。当たり前のように思われるかもしれませんが、図形を見る向きを変える際に、長さの比をとらえ違えてしまうケースが多く見られるのです。実際のテストの際には下の図のように線を色分けすることはできませんが、太線で図形を囲むなどして、視覚的に相似の関係を見逃さないようにしましょう。最後の比の求め方は最小公倍数をスピーディーに求められれば大きな負担はないかと思われます。

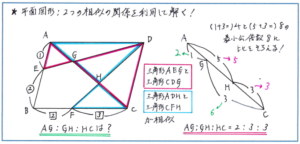
　この2つの相似の関係を使う問題のように、複雑に見えても解き方のパターンを正しく習得していれば得点源とできる問題では、パターンを使えることで急いで解いてしまい、先程挙げました長さの取り違えのような、細かなミスが起きてしまいがちです。解法がパターン化された問題には、より一層ミスが起きないように細心の注意で臨みましょう。

【第3位　運転間隔の問題：運転間隔にあたる部分を図を使って正しく表現できていますか？】

　速さの問題の新出テーマの中で、「運転間隔」の問題は、問題内容を図でするのが難しい単元です。逆に図のかき方、運転間隔を図に盛り込む方法を習得できれば、式は立てやすく、複雑な通過算の問題よりも解きやすくなります。
　例えば、「一定の速さで線路ぞいを走る自転車が、上り電車に12分おきに追いこされ、下り電車と6分おきにすれちがいました。自転車と電車の速さの比を求めなさい。ただし、上り電車と下り電車の運転間隔は同じで、上り電車と下り電車の速さは同じです。また、電車や自転車の長さは考えません。」といった問題。与えられた時間の逆比から、自転車と電車の速さの和と差の比を使って解くという解答方針が定まっているからといって、機械的に6分と12分を当てはめて解いてしまうと、問題の出され方が変化した時に対応できなくなってしまいます。自転車と電車の速さの和と差の比がどのように算出されるのか、それを図を使って理解できていれば、問題の難度が上がっても対応することができます。
　そこで今回の問題の状況を図にすると、下のようになります。

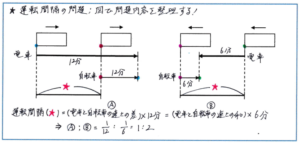
　予習シリーズの図では、バスの長さは表されていません。問題でも「電車や自転車の長さは考えません」と書かれていますので、あえて長さを表さなくてもよいのですが、通過算の考え方を習得した皆さんからすると、電車に追いこされる、電車とすれちがう、といったケースは、簡単に電車の図を入れた方がイメージを持ちやすいかもしれません。追いこされる場合には電車の最後尾に印を、すれちがう場合には電車の先頭に印をつけておく（最後尾と先頭は逆でも構いません）と、どの部分に12分かかり、6分かかったのかを図で把握することができます。あとは、2つの図に共通して、電車間の距離が運転間隔に当たると理解できますので、その運転間隔が、(電車と自転車の速さの差)×12分と、(電車と自転車の速さの和)×6分という2つの式で表せることから、(電車と自転車の速さの差)：(電車と自転車の速さの和)＝1/12：1/6＝2：1とすることができます。最後は、比の和差算の考え方（消去算の考え方でも解くことができます）で、(電車の速さ)：(自転車の速さ)＝(2＋1)÷2：(2－1)÷2＝1.5：0.5＝3：1と求めることができます。
　【第2位】の相似の関係と同じく、速さの問題でもパターンで解く際には機械的に数を当てはめるのではなく、なぜその式が成り立つのかを考える意識をしっかり持つようにしましょう。それが6年算数の応用問題を解く際の重要な前提条件となります。

【第4位　場合の数：難問に対応できるように、複数の解法を身につけておきましょう！】

　場合の数の問題では、解き方を1つに限定せずに、問題内容に応じた解き方のパターンを覚えておけば、難度が高い問題でも正解できる可能性が一気に高くなります。
　例えば、新出テーマの「道順の応用」の問題は、マス目で示された道の、端から端まで最短経路で行く方法を求めるタイプの問題ですが、マス目の端に数字を書き込んで、その和を書き連ねて行く解法がまずは浮かんでくるでしょう。この解法は、計算を機械的に、スピード感をもって進められるメリットがありますので、答えとなる場合の数が少ないケースではとても有効です。
　ただし、マス目の数が多くなり、最終的な答えが3ケタ以上の数になってしまうと、たし算の過程でミスが起きやすくなってしまいます。このパターンの問題は、途中で1つでも計算ミスをしてしまうと、そこから連動して間違いが起きてしまいますので、細かな計算ミスは何としても防がなくてはなりません。かといって、計算の工夫ができるタイプの問題ではありませんので、正確に解く、ということに尽きてしまいます。

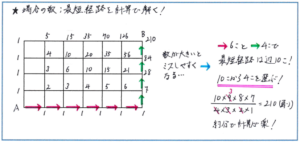
　そこで、別の解法を考えてみましょう。上の図のようなマス目の場合、A地点からB地点まで最短経路で行くには、マス目の辺を横に6個、たてに4個、合計して10個の辺を進めばよいことになります。ここから、10個の辺のうち4個をたての辺にする、という点で、「10個の辺から4個の辺を選ぶ選び方」と考えられるのです。こうなれば、計算は、10×9×8×7/4×3×2×1の式で進められます。この分数式では約分ができる数の組み合わせがありますので、結果、10×7×3＝210と、難度の低い計算で正解まで行き着けるのです。
まずはマス目に書き込むといった基本パターンをしっかり覚え込み、計算ミスが起きやすいケースであると感じられた場合には、別の解法（今回であれば選び方の方法）を使う、という判断ができるように、解法を少しでも多く備えておくようにしましょう。

【第5位　影の問題：どの部分に相似の関係があるかを図で整理できていますか？】

　平面図形の新出テーマ「影の問題」については、相似の関係を利用することが大前提となります。問題文の中で示される例から棒や電灯と影の長さの関係をつかみ、図をかいて（与えられた図にかき込みをして）長さを求める流れとなりますが、シンプルに棒や電灯に影が1つであれば、容易に解答できるところ、例えば、下の図のような段差のあるケースでは、どの部分に相似の関係があるのか、図をよく見て、適切なかき込みをしたうえで把握する必要があります。
　下の図のような場合に影の長さの合計を求めるには、シカクの長さがわかれば解答に一気に近づくことができますが、そこでシカクの長さを相似で解こうとしても、相似の関係を見つけることはできません。ここで図をよく見ると、電灯のＢＤの部分の長さは、(2＋シカク)mになりますので、シカクを求めなくてもＢＤの長さを求めればよいことに気づきます。

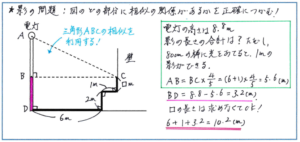
　ＡＢの長さについては、予習シリーズでも出されるような典型的なパターンとして対応できるでしょう。ＢＣの長さが、(6＋1＝)7mのため、相似比の5：4を利用してＡＢの長さが7×4/5＝5.6（m）となります。電灯の高さ（ＡＤの長さ）が8.8mであることから、ＢＤの長さが、(8.8－5.6＝)3.2mとなり、影の長さの合計が、7＋3.2＝10.2（m）と求められます。
　複雑に見える影の図でも、よく図を見て、どの長さを求めればよいかを冷静に整理できれば、補助線が引きやすくなり、得点のチャンスが大きく広がります。図をよく見る意識を高めて練習を重ねましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。