メールマガジン宝箱 Mail magazine

　今回の5年生第7回組分けテストは、「速さと比」、「平面図形と比」といった、「比」を駆使して解く力が試される入試頻出の単元が目白押しのうえ、難問を多く含む「図形の移動」も範囲となる、重厚な内容のテストです。そうした重要単元について、今回のテスト対策を通して確実に理解しておくことが、今後の受験算数を進めるうえでの必須の基盤となり、算数での得点力を大きくアップさせるための大事なステップとなります。そこで、「比」の単元を中心に、第7回組分けテストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！
　さらにこちらの算数予想問題と組み合わせれば、組分けテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　速さと比：「速さと時間の逆比の関係」を正確に使いこなせていますか？】

　今回の組分けテストにおいて、速さと比に関する単元がテスト範囲の半分（第6回・第7回）を占めています。この後にご紹介する「旅人算と比」や、「グラフの問題」と多岐にわたって比を使って解く問題が出されますが、そのすべての基本となるのが、『予習シリーズ5年下』のP.62で示されている「道のりが同じならば、速さの比と時間の比は逆比の関係」というきまりです。この逆比の関係は、道のり＝（速さ）×（時間）の公式から、道のりが一定であれば、速さと時間の関係は反比例になるという考え方から導くことができますが、そうした反比例の考え方を使って導き出すプロセスを経ることなく、問題を見た瞬間に使えるように、「きまり」として徹底的に覚え込んで頂きたいのです。この速さと時間の逆比の関係を使いこなすために逆比の考え方を学んできた、といっても過言ではありません。それほどに、この速さの逆比の関係はこれからのテストや、入試問題でとにかく多く使うことになり、逆比の関係が使いこなせなければ、速さの応用問題は解けないと断言できるほどに必須のものです。それほどに重要極まりない「速さと時間の逆比の関係」を、今回の組分けテスト対策で徹底的に理解してください。

　もちろん、「速さが同じであれば、時間の比＝道のりの比」、「時間が同じであれば、速さの比＝道のりの比」の関係も重要ですので、しっかり覚えて頂きたいですが、例えば計算の逆算もそうですが、小学生のお子様にとっては「逆」の考え方がなかなか使いこなせない、苦手であるといったケースが多いのです。圧倒的に頻出度が高い「速さにおける逆比の関係」ですので、苦手と言ってはいられません。今回の組分けテスト対策では、まずこの逆比の関係を優先的に覚え込んでください。ここが中学受験算数の勝負の分かれ目のひとつと思って、万全の対策を重ねておきましょう。

【第2位　旅人算と比：「折り返しの旅人算と比」の問題内容を線分図で整理できていますか？】

　もともと旅人算の問題で内容を整理するために線分図が有効であることは言うまでもないのですが、比を使って解く問題になると、その有効性がさらに何段もアップします。線分図を使うことで動きのイメージが視覚化されて、与えられた長さや時間の値、そして比の関係をどのように利用すればよいか、といった方針が立てやすくなります。
　さらに旅人算の中でも「折り返し」の問題になると、頭の中だけで動きをイメージすることがとても困難になります。例えば同じ地点を同時に出発した2人のうち、速い方が折り返して遅い方と出会う、といった問題。ここでも線分図を使うと、2人の動きが断然わかりやすくなるのです。この折り返しの線分図がしっかりかけるようになっていれば、比の関係も視覚的にとらえられるようになります。
　例えば下の左の図のように、速さの比が7：5の2人のうち1人が折り返して出会う場合、出会うまでに2人が進む時間が同じですので、「速さの比＝道のりの比」となり、2人が動いた合計の道のりがマル12、片道の道のりが（マル12÷2＝）マル6となり、与えられた240mがマル6－マル5＝マル1となることから、片道の道のりが、240×6＝1440mと求めることができるのです。
　また、右の図のような、出会うまでに6分、出会ってからもとの場所に戻るまでに4分、といった状況であれば、同じ道のりを進むのにかかる時間が4：6＝2：3より、速さの比を1/2：1/3＝3：2と求めることができます。

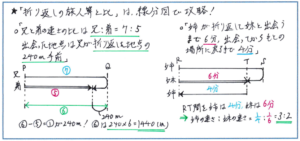
　イメージがしづらい折り返しに比の要素まで入ってくると、問題の難度が大きく上がる印象を持たれがちですが、線分図をしっかり使いこなせば、少ない情報で与えられた数値の関係を正確に求めることができるようになり、スムーズに解き進めることができます。組分けテストは制限時間の使い方もポイントになります。テスト会場で線分図をかくのに時間をかけ過ぎないように、普段から「ていねい過ぎず見やすい」線分図をかく練習を重ねておきましょう。

【第3位　速さとグラフの比：グラフの中にある相似の関係をスムーズに見つけられていますか？】

　今回の組分けテストでは、速さとグラフでも比を使うケースが多く出てきます。ここで求められるのはグラフを見る目です。グラフの中にある相似の関係を見つけること、そして速さや時間の比をグラフのどの部分の長さの比に置きかえればよいかを、的確に判断する必要があるのです。
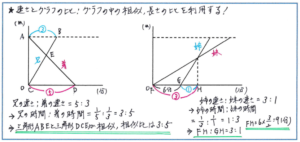
　例えば下の左のグラフでは、クロス型の相似の関係を見つけることができます。今回の組分けでグラフの問題が出てきた時には、まずクロス型の相似の関係がないかどうかをチェックするようにしましょう。この相似の関係が見つけられれば、一気に解答しやすくなります。ここで注意すべきは、グラフの中の相似の三角形に十分な長さが与えられていないことです。あくまで図形ではなく、グラフを読み解く問題ですので、三角形の辺にあたる部分すべての長さが与えられることはありません。
　ここでまた「逆比の関係」が重要な武器となります。2人の速さの比が5：3ということは、同じ道のりを進むのにかかる時間の比は、1/5：1/3＝3：5となり、平行な関係にある2つの長さの比が3：5となるのです。こうして相似比がわかれば、相似の関係をフルに活用して解答を進められるのです。
　また、右の図のように、一方がもう一方に追いつくといった状況がグラフになった場合にも、比を使うことで解き進められるケースが多くあります。姉と妹の速さの比が3：1で姉が6分遅れて出発して妹に追いつくといった場合、やはり同じ道のりを進むのに速さと時間が逆比になることを使えば、姉が妹に追いつくまでの時間の比1：3の差の2が6分にあたることがわかりますので、例えば姉が追いつくまでにかかる時間であれば、6×1/2＝3（分）と求めることができます。

　今回挙げました2つの例は、もちろんグラフではなく線分図を使っても解くことができますが、より複雑なグラフの問題に対応するためにも、シンプルな問題の演習を通して、グラフのどの部分に目をつければよいのか、という意識づけを行っておくことが有効になります。グラフの見方を身につけて、グラフ問題に対する苦手意識がなくなれば、これからの受験算数における、大きなアドバンテージを得ることができます。

【第4位　辺の比と面積比：『予習シリーズ5年下』P.87の「応用公式」を使いこなせていますか？】

　辺の比と面積比の問題では、『予習シリーズ5年下』P.87に掲載されている「応用公式」を徹底的に覚えておきましょう。この範囲では、「相似の応用」や「六角形の分割」といった重要単元が目白押しで、特に相似は頻出度が高いので十分に対策をしておくことがもちろん必須なのですが、この応用公式は、覚えられているかどうかで、得点の差が大きく開いてしまうものです。公式を覚えていなくても、解くことはできるのですが、そこで費やす時間と手間はかなり大きく、テスト全体の制限時間を考えると、得策とは言えません。まさに「公式」となっているように、覚えておくと大きな武器になります。
　気をつけておきたいのが、下の右の図のように「向き」が変わった際です。『予習シリーズ』に掲載されている向きだけで覚えてしまわないように、ブーメランのような形がどの向きになっても正しく比を求められるように練習しておきましょう。

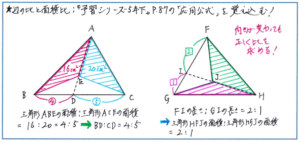
　このタイプの問題を解く際には、比の値や、求めた面積、長さなどを図にかき込むとより解きやすくなりますので、どんどんかき込みをして頂きたいのですが、雑にかいてしまうと、細かい部分が一気に見づらくなる危険性があります。ていねいにし過ぎ必要はありませんが、自分で見て、かき込んだのはどの長さの値だろうか？といった迷いが生じないように、普段から図にかき込む練習をしておくとよいでしょう。

【第5位　図形の移動：細かな長さの取り違いが起きないような図のかき方ができていますか？】

　今回の組分けテストでは、速さと比、平面図形と比といった、「比」に関する重要単元がテスト範囲に含まれていることで、どうしてもそれらの対策にかける時間が多くなってしまうかと思われますが、それによって、この「図形の移動」の対策が不足してしまわないように気をつけましょう。
　図形の移動の中には、「円・おうぎ形の転がり」「図形の平行移動」があり、どちらにも共通して、図の動きを正確につかむために、自分で図をかく作業が必要になります。図形が転がる場合も、平行移動する倍も、だいたいのパターンはつかめているから、図をかかなくても正解できる…と思って頭の中だけで解いてしまうと、思わぬミスが起きてしまいます。転がりの問題であれば「角度」、平行移動の問題であれば「長さ・形」の取違いで正解を逃してしまうケースがとても多いのです。
　特に平行移動では、2つの図形の重なりを求めさせる問題が多いですが、そのどちらかが複雑な図形となって、テスト後半の難問として出される可能性が高くあります。さらには時間と重なる部分の面積の関係を表したグラフと合わせて考察させる問題も多く、ちょっとした長さや形の取り違いが失点につながることが多くありますので、細心の注意が必要です。
　対策としては、図で動きを整理することになりますが、転がりの問題であれば、問題の図にかき込みをしても回転する図形の動きが見えづらくなりませんが、平行移動の問題では、ひとつの図に起こり得るケースをすべてかき込もうとしてしまうと、図形が渋滞した状態になり、正確に長さなどを把握することができなくなります。そうした事態を防ぐために、手間はかかりますが、起こり得る状況に分けた図をかくようにしましょう。状況を分けてかくことで、変化の様子も把握しやすくなり、グラフの読み取りも断然進めやすくなります。

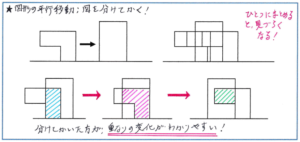
　図をかく際には、くり返しになりますが「ていねいにし過ぎない」ことを徹底しましょう。今回の組分けは「比」に関する問題で解答に時間がかかる可能性が高くありますので、時間配分が重要になります。多少線が曲がっても、自分が必要な値を正確にとらえられれば、それで構いません。ただ、どの程度までラフにかいて構わないのかは、事前に練習しておかなければなりません。テスト当日のぶっつけ本番にならないように、自分で図をかく練習を重ねておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。