メールマガジン宝箱 Mail magazine

6年8月度マンスリーテスト予想問題　現在無料公開中です！

　夏休みの総仕上げとなるマンスリー攻略のポイントをランキングにまとめました！範囲のない実力テストで存分に力を発揮するためにも、ぜひご覧ください！
　また、攻略ポイントだけでなく予想問題付きです。過去問を分析し最も出題される可能性が高い問題を揃えてあります。くわしい解説も準備しますので、問題を解いて終わりではなく、解説を熟読して、解法をしっかり身につけてください。問題は鉄人会のHPで公開しています。クラスアップのためにも、ぜひご活用ください！

予想問題はこちらのページで無料公開中です。

それではランキングの発表です。まずは第5位からです！

【第5位　濃度に関する問題：同じ操作をくり返す問題に対応できていますか？】

　例えば、「濃さが16%の食塩水200ｇから、50ｇの食塩水を取り出して、かわりに50ｇの水を入れるという操作を2回くり返すと食塩水の濃度は何%になりますか」といった問題。1回の操作ごとに濃度を求めていては時間ばかりが過ぎてしまいます。
　ここでは比を使うことがポイントです！操作を何回くり返しても、「水50ｇと食塩水150ｇを混ぜること」は変わりません。そこで1回の操作で濃度がどのように変化したかがわかれば、ほぼ問題を解けたことになります。面積図でも天びん図でもよいので、水と食塩水を50：150＝1：3の割合で混ぜた場合、濃度がもとの食塩水の3/(1+3)＝3/4となることを確かめてみましょう。

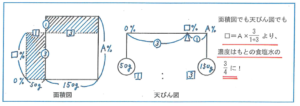
あとは、操作を2回くり返すので、16%×3/4×3/4＝9%と答えを求められます。このやり方がわかっていれば、例えば操作を5回くり返す場合は3/4を5回かけ合せる、と応用させることが簡単にできるのです。比が様々な場面で活用できる強力な武器であることがわかります。

【第4位　場合の数：書き出しと計算をうまく組み合わせましょう！】

　場合の数を苦手とするお子様が多い理由の中に、解き方を特定できないことがあると思われます。言い方を換えますと、書き出して解くのか、計算で解くのか判断しづらい！というところでしょうか。
　もちろん式で解くことができれば、書き出しで起きてしまうような、「書きもれ」はしなくて済みます。ですが、例えば「1から999までの整数のうち、各位の数の和が3である整数は全部で何個ありますか」といった問題を、式だけで対応できるでしょうか。これが5の倍数の個数を求めるのであれば、すぐに式を立てられますが、各位の和、となるとそうはいきません。
　この場合は、各位の数の和が3となる「3個」の整数の組み合わせをまず書き出します。
　（0、0、3）（0、1、2）（1、1、1）の3つとなります。ここからは並べ方の解き方に持ち込むことができるのです。例えば（0、0、3）であれば、003、030、300の3通りの並べ方がありますが、
003 → 3
030 → 30
300 → 300
と考えることができるので、並べ方で求めた場合の数をそのまま使えるのです。
　結果として、
（0、0、3）→3通り
（0、1、2）→6通り
（1、1、1）→1通り
で、3＋6＋1＝10より10個と答えを導き出すことができます。
この問題では、0（ゼロ）の使い方がやや高度ではありますが、まず組合せを書き出して、そこからの並べ方は計算で勝負する！という解き方をマスターすれば、場合の数を攻略する糸口を見つけられるでしょう。

【第3位　平面図形（相似）：角度に気をつけることが攻略の糸口に！】

　今回のテストでも相似は避けて通れないでしょう。平面図形のラスボス的な存在である相似。何とか攻略したいところです。そのためにぜひ気をつけて頂きたいのが「角度」に注意すること！
　もちろん相似の関係にある図形を見つけるためには、「平行な線」が大事であることは言うまでもありません。下の図①のような三角形の1辺に平行な線によって相似の関係が生まれること、また②のような砂時計型の図形が相似であることも平行な線によってつくり出されるものです。

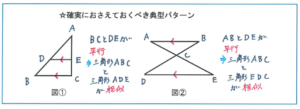
この2つの典型的なパターンはまず必須です！とにかくこの典型は見逃さないことです。そのうえで、ぜひ注意したいのが下の図③、図④のパターンです。

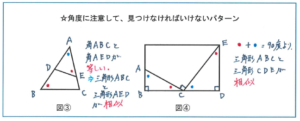
　同じく三角形の中に別の三角形があるパターンでも図①のように、向きまで同じであれば気がつくのに、向きが変わってしまうだけで、見つけられなくなってしまうことが起こりがちです。
　また図④にある相似な関係も意外と気がつかれないことがあります。③と④に共通しているのは「角度」に注目することです。サピックス6年生の8月ともなれば、①②のような典型パターンだけでは対応できない問題が出される可能性が高いです。ぜひ角度に注意して、相似な関係にある図形を見つけ出してください。

【第2位　立体図形（回転体）：回転させる前の平面図形にひと工夫を！】

　回転体の問題の中で、複雑なかたちを回転させるタイプの場合は、回転する前の平面図形に注意しましょう。例えば下の図のような二等辺三角形ＡＢＣを、Ｌを軸として1回転させてできた立体の表面積を求める場合。

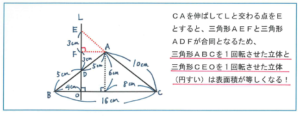
　このようなタイプの問題では、まず回転させてできる立体の見取り図をかくのに時間がかかり、そこから表面積を求める際にも、どの部分が等しくなるのかがわかりづらくなってしまいます。ひと工夫を加えやすい平面の段階からよく図を見て、どの部分が等しくなるのかを考えるようにしましょう。

【第1位　旅人算：図とは内容を「見える化」してくれる便利かつ強力な武器！】

　旅人算の問題になると、塾でも図をかくように指示されることがとにかく多いと思われます。こればかりはどうしても避けられません。特に、サピックスのテストでは大問4以降くらいで出される旅人算は図が必須となります。テスト後半で出される旅人算は、とにかく文章が長い！読んでいるだけで疲れてしまうような問題にこそ図が効果的なのです。
　ここでは基本的な図のかき方の中で、特に気をつけて頂きたい点を取り上げたいと思います。それは「同じ時間に同じ記号を使う」というルールを設けることです。特に「同じ方向から２人、別の方向から１人が同時に出発する」というタイプの問題。複数の出会いが発生するこのタイプの問題で、このルールが効果を発揮します。例えば、「Ｐ地からＱ地に向ってＡ君とＢ君が、Ｑ地からＰ地に向ってＣさんが同時に出発する」とした状況を下の図のように表します。

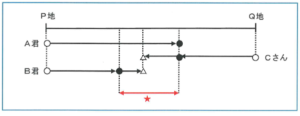
　このように出発時を○、Ａ君とＣさんが出会う時点を●、ＣさんとＢ君が出会う時点を△とすることで、○→●→△という時間の流れで、どのように出会いが起きたのかを視覚的にとらえることができるのです。特にこの問題のポイントとなる、★の部分が、○～●の時間でのＡ君とＢ君の道のりの差であり、●～△でのＣさんとＢ君の道のりの和でもあることが、記号がない状態よりも理解しやすくなります。ほんのひと手間で大きな違いが生まれるひとつの例です。ぜひ試してみてください。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。