メールマガジン宝箱 Mail magazine

　新6年生の皆さん、1月の組分けは比をどれだけ使いこなせるかが、偏差値アップにつながります。
　速さと比では逆比や連比を使いこなし、また容器と水量の問題でも面積比を使うことが、得点力を大きくアップさせます。図形問題やグラフ問題では、相似の関係を速く正確に見つける力が求められます。
問題内容に合わせた比の使い方を実践できるように、対応力をしっかりと鍛え上げておきたいところです。
　そこで、対策ポイントを、プロ家庭教師の視点から第5位から第1位までのランキングのかたちにまとめました。ぜひ偏差値アップ、クラスアップを実現してください！応援しています！
　さらに、このランキングは明日公開の予想問題と連動していますので、予想問題も併せてご活用ください！
予想問題はこちらのページで1週間限定で無料公開します！

【第5位　通過算：問題文の言葉の使われ方に注意して図がかけていますか？】

　通過算の問題では図で問題内容を整理することで、正確に式を立てることができますが、定番のパターンにとらわれて、それ以外のかたちに対応できなくならないように注意する必要があります。定番とは「列車がトンネルに入り始めてから、完全に出るまでに○○秒」というパターンです。
　それ以外のかたちとは、例えば次のような問題です。

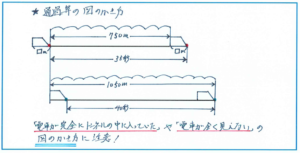
　注意するのは後半の「電車が完全にトンネルの中に入っていた時間」です。「これは電車がまったく見えない時間」と表されることもあります。
　電車が完全にトンネルの中に入っていた時間は、上記の下の図のように表すことができます。「完全に出るまで」の時間が2つあれば、距離の差を時間の差で割る、という解き方を使えますが、このような問題にはどのように対応すればようでしょうか。
　まずは電車の長さを□mとしましょう。上記の2つの状態が以下のような式にすることができます。
　完全に出る：（750＋□）mを35秒
　完全に入っていた：（1050－□）mを40秒
　ここで□に注目すると、上下の式をたすことで□が消えることがわかります。
　（750＋□）＋（1050－□）＝750＋1050
　この道のりを電車が進んだ時間が、（35＋40）秒になりますので、以下の式から電話の早さが求められます。
　(750＋1050)÷(35＋40)＝1800÷75＝24（m/秒）
　式としては単純ですが、なぜこの式になるのかを図を使って理解するようにしましょう。

【第4位　速さと比：逆比と連比を使った解き方を使いこなせていますか？】

　速さと比の問題の中で、「毎分180mの速さで行くと始まる時刻の20分前に着き、毎分80mの速さで行くと始まる時刻の5分前に着きます。」というパターンであれば、速さの比と時間の比の逆比関係を使って解くことがすぐに思いつくでしょう。
　それが次のような問題では、どのように対応すればよいでしょうか。

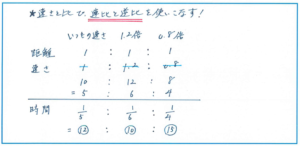
　問題を見た瞬間に、逆比を使うことは頭に浮かんできますが、「いつもの速さ」「1.2倍の速さ」「0.8倍の速さ」の3種類の速さがあった場合には、どのように解き進めればよいのか。
　上記のような連比を使うことで、10分をどのように扱えばよいのかが見えてきます。
　いつもの速さ：1.2倍の速さ：0.8倍の速さ＝10：12：8＝5：6：4
より、かかる時間の比が、1/5：1/6：1/4＝12：10：15
となることから、10分が比の2にあたることから、10÷2×3＝15（分）と答えに行き着くことができます。
　3種類の速さになっても、逆比を利用することには変わりありません。あとは連比を速く正確に使うことができるように注意しましょう。

【第3位　容器と水量：高さの比と底面積の比の逆比の関係を理解できていますか？】

　相水の入った容器におもりを沈める問題では、水位が変化した分がどの部分と同じになるかを把握しなければなりません。次のような問題で考えてみましょう。

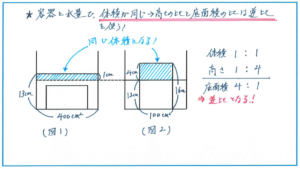
　まずは水量の変化を把握するために、断面図を利用する解法を思い出しましょう。立体図形のままに頭の中で解こうとすると、式の過程でミスが起こってしまいがちです。
　上記の図では斜線をつけた部分の面積が同じになることは、この問題解くための最初のポイントです。これは水位の変化では基本にあたりますので、確実に理解できるようにしておきましょう。
　あとは比を使って解いていきます。斜線の部分の面積が同じ（水量の体積が同じ）になることから、この2つの長方形の縦の長さと横の長さ（高さの比と底面積の比）が逆比の関係になります。（図1）の斜線部の縦は1（cm）、横は400（平方cm）、（図2）の斜線部の縦は(16－12＝)4（cm）になりますので、横は1×400÷4＝100（平方cm）となります。
　正方形の面積が100平方cmなので、1辺の長さが10cmと求められます。
　まずは断面図をかき、そこから逆比の関係を利用する、という流れの解き方をしっかりと覚え込んでください。

【第2位　平面図形：三角形が合同になる条件を確認しておきましょう！】

　平面図形の問題を解く際に、三角形の相似条件はしっかり覚えられているのに、合同条件になるとあやふやになってしまうケースが多く見られます。もちろん塾でも学習はしていますが、徹底して覚えるところまで至っていないことがあるのです。
　確実に覚えられていれば問題ありませんが、ここで一度、三角形が合同になる条件を覚えられているかどうかを確認して、少しでも曖昧であった場合には、くり返し言い唱える、実際に合同な三角形をかいてみる、といった方法で覚え込むようにしましょう。

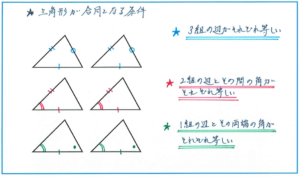
【第1位　場合の数：ぬり分け問題で、場合分けが確実にできていますか？】

　場合の数の問題の中でも、ぬり分けの問題は、場合分けや計算を駆使する点で難度が高いと言えます。それだけに得点できれば差をつけられる問題ともなります。
　次のような問題を考えてみましょう。

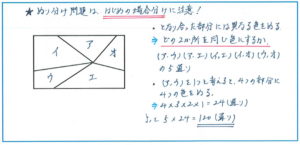
　このように、ぬる場所の数よりも色が少なくなる場合には、となり合った部分には異なる色をぬることに気をつけて、どの2か所を同じにするかを場合分けしましょう。
　この問題では、（ア、ウ）（ア、エ）（イ、エ）（イ、オ）（ウ、オ）の5通りになります。この場合分けでもれがなくすることが、正解するためには十分に気をつけなければいけません。
　ここからは計算で進めて行きます。例えば（アとウ）を1つと考えると、4つの部分に4つの色をぬるというかたちにできますので、ぬり方は4×3×2×1＝24（通り）になります。
　最後に、この24通りが、最初に場合分けした5通り全てにあてはまりますので、24×5＝120（通り）となります。
　場合の数は解き方が定まらないと、時間がかかり、正答率も低くなってしまいます。問題をよく読み、条件を整理して場合分け（書き出し）と計算を組み合わせる練習をしましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。