メールマガジン宝箱 Mail magazine

　今回の5年生第8回組分けテストは、「立体の切断」、「水深の変化」といった、立体図形で「比」を利用した解き方をどこまで使いこなせるかを試す、入試頻出の難問が多く含まれます。もともと難度の高い立体図形に比までからむという難敵ですが、解法さえしっかりつかんでおけば攻略の一口が確実につかめます。その他にも「ニュートン算」を含む仕事算や、素因数分解を使う数の問題など、重要単元が目白押しの今回の組分けテストの対策を万全に進めることは、そのまま今後の受験算数を進めるうえでの重要な足場づくりとなります。そこで、第8回組分けテストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！
　さらにこちらの算数予想問題と組み合わせれば、組分けテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　立体の切断：自分の手で切断面をかいて切断のルールを確認しておきましょう！】

　今回の組分けテストの範囲の中でも「立体の切断」は、解答に時間のかかる問題が多く、解答方針をしっかり立ててスムーズに作業を進めることが必須となります。この単元は、かつては男子難関校以外で出題されるケースは少なかったのですが、近年では偏差値に関わらず多くの学校で出題されますので、今回の演習で基本をしっかり固めておく必要があります。
　切断に関する基本的なルールは、『予習シリーズ5年下』の150ページから154ページまでに詳しく示されていますので、この部分をじっくりと読み込んで、立方体や直方体に自分で切断面をかき込む練習を重ねておきましょう。特に重要なのが、150ページに掲載されている「平行な2つの平面に、別の平面が交わってできる2本の直線は平行になる」というルールです。このルールにしたがって、立方体や直方体に切断面が入った際に、面に正しく平行線がひけるかどうかを、151ページ以降の例題で試してみてください。
気をつけて頂きたいのが、イメージで平行線をひかないことです。『予習シリーズ』の各例題の解説にもありますが、見た目で平行な線をひくのではなく、三角形の相似の関係を利用して、立体の辺上に正しい長さで点を打つ、という流れを必ず守ってください。
　立体図形の難しさは、見えない部分がどのようになっているのかを正確に把握するところにあります。その点、この切断の単元では、相似を利用するといった明確な方法がありますので、相似比を的確に使って切断面をつくる練習を重ねましょう。

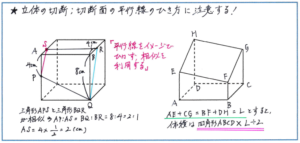
　また、『予習シリーズ5年下』の155ページに掲載されている、「切り口が平行四辺形の場合、向かい合う辺の高さの和が同じ」というルールも使いこなせるようになっておきましょう。このルールを使って、辺の長さや、体積を求めさせる問題をスムーズに正解することが、切断の単元での得点を高く安定させるポイントになります。辺の向きが見えづらい時には、底面となる面を下にして考えてもよいでしょう。焦って辺の長さ取り違いといったミスを起こさないように注意してください。

【第2位　立体の切断：相似比から求められる体積比を正確に利用できていますか？】

　【第1位】に続いて立体の切断について、切断によってできた立体の体積を求める際に、「体積比」を使って解く方法を使えるかどうかが、解答にかかる時間、正確さに大きな違いを生むポイントになります。
　立体を切断する面が台形、五角形、六角形になるような場合の体積を求めさせる問題は、頻出度がとても高いです。これらの場合、切断面の辺を延長して、もとの立体の外側に新たな立体をつくる、「角（つの）出し」とも呼ばれる方法を使って解きますが、ここでの立体の体積を求める際には、「立体の相似」を利用する解法が有効となります。大きな三角すいの体積から、小さな三角すいの体積を除いて求める流れですが、『予習シリーズ5年下』の157ページでも解説されているような、「相似比がa：bであれば、体積比は(a×a×a)：(b×b×b)となる」という関係を踏まえて計算を進めると、大きな三角すいの体積から、小さな三角すいの体積の合計を引くという「引き算」で進めるよりも式を断然簡単にすることができ、計算も楽になります。結果、計算ミスが起こる可能性を低くすることができますので、ぜひ相似を使った解法を覚えておいてください。

　【第1位】での平行線のひき方、そして第2位での体積の求め方に共通するのは「相似」を利用することです。この「立体の切断」が入試問題でも頻出である理由のひとつは、中学受験算数の最重要単元である「比」を図形分野でも正確に使いこなせているかどうかを確かめるのに適しているからだと言えます。これまで習ってきた「図形と比」の解法を総動員して、重要単元である「立体の切断」を攻略することが、今回の組分けテストだけでなく今後のテストでの偏差値アップにつながりますので、しっかり理解を固めておきましょう。

【第3位　水深の変化と比：容器を正面から見た断面図を使った解き方を使いこなせていますか？】

　容器に水を入れたり、おもりを沈めたりする「水深の変化」の単元には様々なタイプの問題がありますが、特に仕切りのある容器に水を入れるタイプの問題は、比を使って解くこともあり、テストで出題されるケースが多くなります。そのほとんどが、水を入れた時間と水深の関係を表したグラフが提示され、グラフから水深が変化する様子を的確につかむ力が求められるものです。
　こうした問題では、まず変化の様子をつかむために、容器のかたちそのままに考えるのではなく、容器を正面から見た断面図で考えることが重要になります。真正面から見た容器の奥行きが同じ長さであれば、水の体積は、それを奥行きで割った面積で考えることができます。奥行きを考えないことで、水の体積を面積として、容器の底面積を辺の長さとする、いわば三次元を二次元とすることで、変化の様子がわかりやすくなるのです。これは奥行きの長さが変わらないことを前提としていて、奥行きが異なるような、いびつなかたちの容器を使う問題が出された場合は、断面図を使って考えることはできませんが、そうした問題が出されるケースは非常に少ないので、まずは断面図を使った解法をしっかり身につけておくとよいでしょう。
　そして次のステップとして、グラフで示された「時間」を断面図の中にかき込んでいきましょう。水が一定の割合で入れられる場合は、かかった時間の比と体積の比（断面図の面積の比）が等しくなりますので、具体的な体積（断面図の面積）を求めることなくして、長さを求めることができます。
　断面図を自分でかく手間こそかかりますが、立体をかくのではなく、とてもシンプルな長方形をかくに過ぎませんので、速く正確に水深の変化を把握するために、またテスト会場で落ち着いて断面図をかけるようになるためにも、練習を重ねておいてください。

　今回の組分けテストの範囲の中で、「立体の切断」「水深の変化」という立体図形の単元では、どちらも「比」を的確に利用する力が求められます。難度の高い問題が多い単元ではありますが、比を使った解法をしっかり身につけておけば、差をつけられる問題にすることができます。難度の高い立体図形の問題を比で攻略する力を今のうち習得しておくことは、今後の算数の対策を進めるうえで、大きなアドバンテージになります。ぜひ立体図形での比の利用方法をじっくりと復習しておきましょう。

【第4位　整数の分解と構成：周期を使った解法を覚えられていますか？】

　既約分数や、素因数分解を使って解く問題が対象となるこの単元では、解き方を選び間違えてしまうと、想定外に解答に時間がかかり、かつ間違いが起きやすい事態になってしまいます。ミスを起こさないような解法を、幅広く習得しておくことがポイントになります。
　例えば「1から200までの整数のうち、2でも3でも5でも割り切れない整数は何個ありますか」といった問題について、まず浮かぶのは集合のベン図を使った解き方でしょう。もちろん正しくベン図がかえれば全く問題のない解法ですが、2、3、5それぞれの倍数、2と3の公倍数、3と5の公倍数、5と2の公倍数と、求めるべき値の種類がかなり多くなってしまいます。そのうえで、導いた値がベン図のどの部分にあたるのかを正確に求める、といった作業量が多い解法となるため、ミスが多くなってしまいがちです。
　そこでぜひ習得して頂きたいのが、「周期」を使った解き方です。今回の問題であれば、2と3と5の最小公倍数である30を1つの周期として、1から30までに「2でも3でも5でも割り切れない整数」が何個あるか調べて、その周期が1から200までに何個あるか、といった流れで解く方法です。まず、その周期をなぜ使えるのかですが、例えば1から30までで条件に合う「17」という数について。17に30を加えた47もまた条件に合います。47＝17＋30として、(17＋30)÷3と分配法則を使うと、17÷3＋30÷3となり、前半の17÷3はわり切れず、後半の30÷3はわりきれる、となりますので、17に30の倍数を加えた数は必ずわり切れないとわかるからなのです。
　そのうえで解き方として気をつけて頂きたいのが、数を整理する方法です。『予習シリーズ5年上』の13ページに掲載されている表は内容を理解するうえではとてもわかりやすいのですが、同じような表をテストの時間内に作成することはかなり難しくなります。そこで、少しでも作業量を減らすために、まずは「2の倍数でない」という点から、1から30までの「奇数のみ」15個を書き出します。その15個から3の倍数と5の倍数を斜線で消していけば、条件に合う数を求めることができます。

　気をつけて頂きたいのが、最後の181～200の20個について忘れずに数え上げることにあります。せっかく効率的な解法で進めても、詰めの部分で間違えてしまっては正解に行き着くことができませんので、最後まで気を緩めずに解き進められるように、注意深く問題に臨んでください。

【第5位　ニュートン算：線分図で問題内容を整理すれば得点のチャンスが大きく広がります！】

　ニュートン算は、問題文が複雑に見えるために難度が高い印象を強く持たれがちです。確かにニュートン算ならではの解き方が身についていないと、どこからどのように解き進めればよいかがわからなくなってしまいますが、線分図を使って問題内容を正確に把握できれば、得点源にできる可能性が一気にアップします。というのもニュートン算は出題のされ方がパターン化されていますので、問題を見てニュートン算の考え方を使えばよいと判断しやすいのです。まずはニュートン算の出題パターンを頭の中にしっかり植え付けて、線分図のかき方を習得しておきましょう。
　まずは正確な線分図がかけるかどうか、チェックしておきましょう。例えば、「毎日一定の割合で草が伸びる放牧場があります。この放牧場で、牛9頭を放し飼いにすると35日で生えている草がなくなります。また、牛15頭を放し飼いにすると14日で生えている草がなくなります。この放牧場で、牛25頭を放し飼いにすると、何日で生えている草がなくなりますか」という問題。

　線分図のかき方の基本パターンをおさえておきましょう。まず、上のように2本の線分図をかき、それぞれの左端にもともとあった量（この問題では、もともと放牧場に生えていた草の量）を置きます。次に単位量あたりに減る量をマル1、増える量をシカク1とします。
　ここで、「線分図の差からマル1とシカク1の関係を式にして、どちらかの記号に統一する」ことがニュートン算攻略の最大のポイントです。
　牛9頭を放し飼いにした場合は、35日で牛が食べる草の量がマル315、牛15頭を放し飼いにした場合は、14日で牛が食べる草の量がマル210となります。
　線分図の長さの差を、マルとシカクで表すことで、マル315－マル210＝シカク35－シカク14より、マル105＝シカク21からマル5＝シカク1となります。
　そこで記号をマルで統一すると、もともと放牧場に生えていた草の量がマル315－マル5×35＝マル140と表せることになります。
　最後に、牛25頭が1日に食べる草の量がマル25、1日に生える草の量がマル5となることから、140÷(25－5)＝7より7日と答えが求められます。
　ニュートン算では線分図が必須アイテムにはなりますが、どの問題でも線分図が必要ということではありません。もともとあった量（上の問題であれば、もともと放牧場に生えていた草の量）がわかっているケースであれば、図をかかなくとも式で正解まで行き着くことができるケースがあります。問題内容によって、よりスピーディーに、かつ正確に解ける方法を身につけておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。