メールマガジン宝箱 Mail magazine

　今回の5年生12月度マンスリーテストでは、「和と差に関する問題」「倍数算」、そして「相当算」と、割合と比を使った文章題が集中してテスト範囲になります。これらの問題では、線分図を中心とした図をいかに正確に速くかけるかが得点をアップさせるポイントになります。問題を読んでどのような図を選ぶかの判断力をこのマンスリー対策を通じて鍛えておくことが、クラスアップ、そして今後の算数での偏差値アップを実現させるために必須となります。そこで、「割合と比の文章題」を図で攻略する方法を中心に、12月度マンスリーテストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！
　さらにこちらの算数予想問題と組み合わせれば、マンスリーテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　和と差に関する問題：人数の異なる過不足算は図を使うと一気に解きやすくなります！】

　和と差に関する問題の中で、特に注意が必要なのが「過不足算」です。基本的な問題であれば、パターンにあてはめて式を立てることが簡単にできますが、「長いす型」と呼ばれるような、いすに座る人数が余ったり、いすが余ったりするタイプの問題では「あまり」の考え方を慎重に進める必要があります。さらに難度が高いのが、「人数が異なるタイプ」の問題です。
　例えば「用意したミカンを何人かの子どもに配ります。男子に4個ずつ、女子に2個ずつ配ると20個あまり、男子に2個ずつ、女子に6個ずつ配ると8個あまります。男子は女子より2人多いです。ミカンは全部で何個用意しましたか」という問題。これを通常の過不足算のパターンにあてはめようとしても、男子と女子の人数の違いをどのように処理すればよいのかが難しく、行き詰まってしまいます。
　そこで図を利用して解き進めるのですが、ポイントは「人数をそろえること」です。2人多いという男子の人数を女子にそろえて、男子2人が持っていたミカンの個数をあまりに加えます。2人の男子には一旦席を外してもらい、持っていたミカンをあまりのミカンが入っている箱に戻す、といったイメージがわかりやすいでしょう。この「あまりの数を変化させるところ」を正確に処理できれば、問題の難度は一気に下がり、スムーズに解き進めることができるようになります。この人数を合わせる過程を表したのが下の図です。

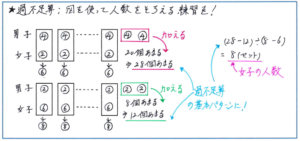
　人数さえそろえば、男子と女子をセットにして、1セットに「男子の4個＋女子の2個＝6個」の6個ずつ配ると、あまりが20＋4×2＝28（個）になり、1セットに「男子の2個＋女子の6個＝8個」の8個ずつ配ると、あまりが8＋2×2＝12（個）になりますので、ここからは通常の過不足算の考え方で、(28－12)÷(8－6)＝8（セット）より、男子と女子が8セット、つまり女子の人数が8人、男子の人数が8＋2＝10（人）とわかります。これよりミカンの数は、4×10＋2×8＋20＝76（個）と求められます。
　このタイプの問題のように、基本型からひと工夫が加わった応用型の問題を、基本型に戻して解く力を求める問題は、今後のサピックスのテスト、そして入試でも多く出題されます。図を使って応用型から基本型に戻す流れをしっかり理解しておきましょう。

【第2位　相当算：「多く」、「少なく」が混ざる場合には線分図で整理しましょう！】

　相当算の問題で確実に正解を手にするためには、線分図の活用が必須となりますが、特に具体的な数値について「多い」と「少ない」が混ざって提示される場合には、線分図を使うことでミスが起こる可能性を大きく下げることができます。
　例えば「ある本を1日目に1/4より18ページ多く読み、2日目に残りの3/5より12ページ少なく読んだので、残りが36ページになりました。この本は全部で何ページありますか」といった問題。複雑な数字が出てこないからといって、頭の中でイメージを立てて解こうとすると、思わぬミスを起こしてしまいます。特に18ページ多い分、12ページ少ない分をどのように扱うかの判断は、イメージだけでは進めづらくなります。
　そこで線分図で視覚的に数の大小を把握できれば、式をスムーズに立てられるようになります。線分図をかく際には、多い分や少ない分について、長さはおおよそで構いませんので、線分図のどこにかき込むかに注意して、数字が見やすくなるようにかき入れることに注意しましょう。相当算に限らず、線分図はていねいにかき過ぎないように、必要な情報を見やすく提示できるようにかく練習を重ねて、慣れておくようにしてください。慣れれば短時間で正確な線分図がかけるようになります。

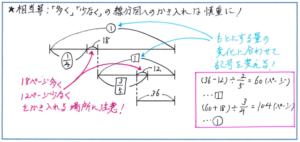
　この問題であれば、1日目に読んだ1/4と、2日目に読んだ3/5の「もとにする量」が変わることは理解しやすいと思われます。マンスリーでもそうした変化については理解を前提に、「多く」と「少なく」を混ぜるといったワンランク難度が高い問題が出される可能性がとても高いです。細かなミスがないように、線分図のかき方を練習しておきましょう。

【第3位　年令算：人数が3人以上になった場合も正確に対応できていますか？】

　年令算の問題では、人数が「母と娘」など2人のみの場合であれば、年令の差が変わらないことを利用して線分図で問題内容を整理すれば、基本的な解答パターンにあてはめて正解に行き着くことができます。
　それに対して人数が3人以上になると、問題の難度が一気に増します。例えば、「現在、父は38才、母は36才、春子さんは13才、弟は10才です。両親の年令の和が2人の子どもの年令の和の2倍になるのは何年後ですか」といった問題。線分図をかこうと考えても、2人分の年令の増加をどのように図で処理すればよいのか戸惑ってしまいます。
　大事なのは、1人分の年令が増えるペースは1年に1才であること。当たり前のように思われるでしょうが、このルールは人数が何人になっても年令算の最重要ポイントであることに変わりありません。そのルールにしたがって、求める年数をマル1として問題内容を式で整理すれば、スムーズに解き進めることができます。
　マル1年後の両親の年令の和、2人の子どもの年令の和を式で表すと、次のようになります。
　　両親の年令の和…38＋36＋マル1×2＝74＋マル2
　　2人の子どもの年令の和…13＋10＋マル1×2＝23＋マル2
　ここで、両親の年令の和が2人の子どもの年令の和の2倍ですので、
　　74＋マル2＝(23＋マル2)×2
　　　　　　　＝46＋マル4
　この式から、74－46＝28がマル4－マル2＝マル2にあたることから、マル1＝28÷2＝14より、14年後と答えを求めることができます。

　実際に14年後の4人の年令は、父が52才、母が50才、春子さんが27才、弟が24才となり、父＋母＝102（才）、春子＋弟＝51（才）で問題の条件の通り、102÷51＝2（倍）となります。年令算は確かめも行いやすいので、スピーディーに見直す練習もしておくとよいでしょう。複雑に見える年令算も、マル1を活用して、倍数算の考え方を使えば解法が見えてきます。

【第4位　倍数算：倍数変化算で比例式を立ててからの計算を正確に行えていますか？】

　倍数算の中で、例えば2人の所持金が同じ金額だけ増えたり減ったりするような「差が一定」の問題や、合計金額は変えずに2人の間でお金のやりとりをするような「和が一定の問題」は、線分図を正確にかければ、正解に行き着くまでに大きな負担はないでしょう。
　それに対して、和も差も一定でない、「倍数変化算」は、比例式を立てて解き進めるという計算力が求められる点で特徴的です。
例えば、「Ａ君とＢ君の所持金の比は7：5でしたが、Ａ君は500円もらい、Ｂ君は100円使ったので、2人の所持金の比は3：1になりました。初めのＡ君の所持金はいくらでしたか」といった問題。
　このようなタイプの問題で、比例式を立てるところまでは、問題内容を忠実に式にするだけですので、容易に進められるでしょう。
　Ａ君とＢ君の初めの所持金を、マル7、マル5とすると、
　(マル7＋500)：(マル5－100)＝3：1
　ここで比例式の内項の積と外項の積が等しいことを利用して、下のような式を立てます。
　(マル7＋500)×1＝(マル5－100)×3
　マル7＋500＝マル15－300
　むしろ気をつけておきたいのが、ここから、マル15－マル7＝500＋300の式へとつながるところにあります。数学の移項の考え方にあたりますが、移項を知らなくても、式の両辺に同じ数を加減しても等式関係は変わらないという考え方をすれば、下のように式を変換できます。
　マル7＋500＋300＝マル15－300＋300
　マル7＋800＝マル15
　マル7＋800－マル7＝マル15－マル7
　800＝マル8
　ここで下のように、式の変換をより視覚的にとらえる方法として、線分図を使う方法があります。

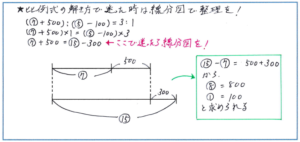
　必ずしも線分図を使わなくてはいけないケースではありませんが、式の変換を苦手としているお子様にとっては、視覚的なイメージを伴って理解を促すことができる利点がありますので、ぜひ試してみてください。

【第5位　相当算の基本：全体の数の置き方によって、解答スピードが大きく変わってきます！】

　相当算の中で、例えば「あるクラスの男子の人数はクラス全体の人数の5/12 よりも2人多く、女子の人数はクラス全体の人数の11/14 よりも26人少ないです。このクラスの生徒は全部で何人ですか」といった問題は、基本的な問題の範疇に入ります。確かに問題文の分量は少なく、シンプルな構成に見えますが、いざ解こうとすると、具体的な人数（2人多い、26人少ない）の処理の仕方を正確に行わなければ、ミスにつながってしまいます。こうした問題では、全体の人数をマルで表して、男子、女子の人数をマルと具体的な数字を使って表し、あとは式を立てて解き進めるかたちになりますが、ここで全の人数の表し方によって、解答のスピード、正確さが大きく変わってきます。多く使われる、「全体を1とする」パターンで進めてもよいのですが、その場合、男子の人数がマル5/12＋2（人）、女子の人数がマル11/14－26（人）と表され、計算を進めると5/12と11/14を通分する過程で分母が84と大きな数になってしまいます。問題によっては分母が100を超える分数を使うことになってしまい、計算の負担が大きくなってしまいます。
　そこで、全体の数をマル84としてしまえば、男子、女子の人数を表すマルも整数となり、断然計算が進めやすくなります。この全体の量を1ではなく最小公倍数にそろえる方法は、仕事算でも使うことが多くあります。計算が得意なお子様でも、苦手なお子様でも、分数より整数の方が計算しやすいことは共通しているでしょう。今回ご紹介したようなタイプの問題は、マンスリーでは中盤の小問として出される可能性が高く、より速く正確に解く力が求められます。そのためにも問題を見てすぐに「全体を1とおく」とするのではなく、より簡単な方法がないか考える習慣をつけておきましょう。

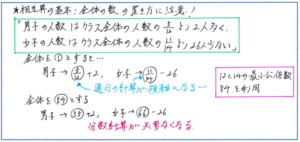
　今回ご紹介したタイプの問題は、もちろん線分図を使って解くこともできます。その方法に慣れている場合はもちろん図を使うことをおすすめしますが、男子は人数が割合で表した数より多く、女子が少ない、といったパターンでは、線分図のかき方が難しくなります。相当算だから線分図と決めつけずに、柔軟に対応できるように、解法の幅を広げておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。