メールマガジン宝箱 Mail magazine

　5月度マンスリーテストは、既約分数の和や水位の変化の問題など、パターン化された解法を正しく使いこなす力が求められるテストです。ただ闇雲に解法を暗記するだけでは、問題の難度が少し上がるだけで対応できなくなってしまいますが、解法の成り立ちさえしっかり覚え込んでおけば、得点源にできる問題を一気に増やすことができます。

　そこで解法の成り立ちに注目して、6年5月度マンスリーテストの対策ポイントを第1位から第5位までランキングにしましたので、ぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの算数予想問題と組み合わせれば、組分けテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　立体図形：表面に色をぬる問題では、ぬられた面の数で立体の位置の把握を！】

　立体図形の中で、「表面に色をぬる問題」では、小さな立方体を積み重ねて、大きな立方体や直方体にしたかたちに色をぬるタイプの問題で、解法を確実に身につけておきたいところです。

　大きな立体に色をぬった後に、小さな立方体のいくつの面に色がぬられているかが問題対象となった際に、大きな立体の角（カド）に位置する立方体には「3つの面」がぬられることはイメージがしやすいでしょう。また、どの面にも色がぬられない立方体も、大きな立体の表面に一切出ていない、「かくれた部分」に位置するとスムーズに把握できます。

　ポイントになるのは、「1つの面」そして「2つの面」に色がぬられた小さな立方体がどこに位置するかを確実につかんでおくことにあります。特に「2つの面」の場合は、大きな立体の「辺の部分」に位置することを利用して、以下のような問題が出されることがあります。

　「2つの面がぬられた立方体の個数が96個になるとき、大きな立方体を辺を何等分しましたか」といった問題です。

　2つの面がぬられた立方体の位置が下の図の赤の部分にあたり、赤の部分は立方体の辺の数と同じく12個あることから、1つの赤の部分に含まれる立方体の数は、96÷12＝8（個）、求めるのは「何等分か」なので、両端の青の立方体も加えて、8＋2＝10（等分）となります。

　「2つの面」「1つの面」がぬられる立方体の位置がしっかり把握できていれば、このタイプの問題に対応しやすくなり、得点源にできます。まずは小さな立方体の位置関係をつかんでおくようにしましょう。

【第2位　くるった時計：どの時刻を比較するか正しく設定できていますか？】

　「2量の関係」の中の「くるった時計」は、問題内容が複雑に見えますが、解法のパターンをしっかりおさえられていれば正解に行き着くまでに大きな負担はかかりません。ただし、問題に出てくる時刻が複数あり、どの時刻を比較するかを間違えてしまうと、正答できる可能性が大きく下がってしまいます。

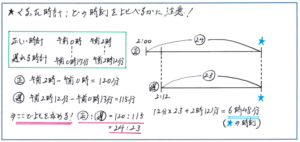
　例えば、「ある時計は一定の割合で遅れます。この時計は、ある日の午前0時に0時17分を、同じ日の午前2時に2時12分をさしていました。この時計は、この日の午前何時何分に正しい時刻をさしますか」という問題。

　ここでは正しい時間の経過と、遅れる時計の時間の経過を比で表して解き進めるのですが、まずは、正しい時計の午前0時と、午前2時での2つの時計がさした時刻を比較します。下のように時間の経過をたてに並べて比べるとわかりやすいでしょう。そこで、正しい時計の、「午前0時から午後2時までの2時間」で、くるった時計が進んだ時間が「午前0時17分から午前2時12分までの1時間55分」となります。

　ここで、正しい時計とくるった時計が同じ時間内で進む時間の比が、120：115＝24：23となることから、下の図のように、くるった時計が正しい時刻をさすまでの時間の差である12分が、24と23の比の差1になるため、求める時刻を、2時12分＋12分×23＝6時48分と求められます。

　今回ご紹介した問題は一方が正しい時刻をさす時計ですが、問題によっては2つの時計ともにくるった時刻をさすケースもあります。それでも解き方の方針はかわりませんので、比較する時刻を定める→2つの時計の進む速さの比を求める→図で整理する、の流れで解き進めるパターンをしっかり練習して習得してください。

【第3位　立体図形：水位の変化は比のかけ算を使って攻略しましょう！】

　立体図形の「水位の変化」の問題では、正しく比を使うことで解答時間を短縮でき、正答率を圧倒的に高くすることができます。注意しておきたいのが、「比のかけ算」の利用です。

　例えば、「下の図のような、同じ高さの円柱をした容器A、Bがあります。底面の直径は、Aが12cm、Bが16cmです。AとBに同じ体積の水を入れたところ、Aの水面の高さは20cmになりました。AとBの間で水を移して、AとBの水面の高さが同じようにすると、その高さは何cmになりますか」と言った問題。

　ここで注意すべきは、実際の水の体積を求めないことです。容器Aの底面の直径が12cmで高さ20cmまで水が入っているので、水の体積が、6×6×3.14×20で求められ、容器Bにも同じ体積の水が入っているのでそれを2倍して、底面積の和で割る…といった方針も間違っていませんが、計算が複雑でミスが起こりがちです。

　底面の直径の長さの比が、12：16＝3：4であることから、底面積の比が3×3：4×4＝9：16になるので、容器Aの底面積をマル9として、2つの容器の水の体積の合計が、マル9×20×2＝マル360となり、それを底面積の和、マル9＋マル16＝マル25で割って、マル360÷マル25＝14.4（cm）として解き進めることができます。

　問題で、底面の直径から高さまで数値が与えられていると、つい計算で解いてしまいたくなりますが、3.14計算をまとめるといった工夫をしても、時間がかかり、計算ミスが起こりがちという状況に変わりはありません。比の計算を使うことで、数値を小さくおさえ、式の数も少なくすることができます。比を使う解き方をテストまでに確認しておきましょう。

【第4位　小数・分数：既約分数の和で対称性を利用できる理由を理解できていますか？】

　「小数・分数」の中で、既約分数の和を求める問題では、「両端の分数から2つずつ組にする」という解法を教えられ、実際にその方法で解き進めることで、解答スピード、正答率ともに高くできることを体感されているでしょう。

　ただ、なぜこの解法が成り立つのか、その理由をしっかりつかんでおかなければ、問題の難度が上がった際にスムーズに対応できなくなってしまいます。ここでは、以下の問題を例として、解法の成り立ちを確認しておきましょう。

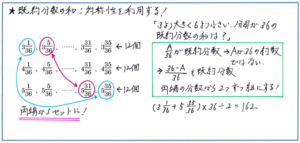
　「3より大きく6より小さい、分母が36の分数について、約分できない分数の和はいくつになりますか」といった問題です。

　まず、0から1までに分母が36の既約分数がいくつあるかについては、迷うことなく正解に行き着きたいところです。36を素因数分解すると、2×2×3×3となるので、分子が2の倍数でも3の倍数でもない場合が既約分数になります。ここからは集合の考え方で、2の倍数が36÷2＝18（個）、3の倍数が36÷3＝12（個）、2と3の公倍数が、36÷6＝6（個）となり、2または3の倍数が、18＋12－6＝24（個）のため、既約分数の個数は、36－24＝12（個）となります。

　ここで、1/36から35/36の既約分数について考えた場合、A/36が既約分数であれば、分子のAは36の約数ではなくなります。よって、(36－A)/36の分子（36－A）もまた36の約数ではなくなります。Aに1を入れれば、1/36と35/36はどちらも既約分数に、Aに5を入れれば5/36と31/36はどちらも既約分数になるのです。

　こうして、「両端の分数から2つずつ組にする」という考え方が成り立ちます。この問題のように、「3と1/36」と「5と35/36」を組にするのも、帯分数の分数部分に着目すれば「両端の分数から2つずつ組にする」の考え方を使うことができるためです。後は、既約分数が全部で、12×3＝36（個）あるので、(3と1/36＋5と5/36)×36÷2＝162、と解き進めることができます。

　マンスリーテストで解法の説明をさせる問題が出されることは想定できませんが、解法の成り立ちを理解できているかどうかで、解答の確実さに大きな差が生まれます。この単元に限らず、機械的に覚えてしまいがちな解法については、その成り立ちをしっかり確認しておきましょう。

【第5位　タクシー料金タイプのグラフ問題：加算の回数を正しく計算できていますか？】

　「2量の関係」の中では、様々なグラフを扱いますが、その中でもグラフが階段のような形になる、タクシー料金タイプの問題は、マンスリーテストで出題される可能性が高くあります。パターン化された解き方を実践できれば、得点源にできる問題ですが、解法の理解が曖昧なままでは細かな数値を間違えてしまう危険性が高くなってしまいます。最後の詰めまで解法の覚え込みが甘くならないように注意しましょう。

　例えば下のような「電報の電文の字数と料金の関係」を表したグラフで考え方を整理してみましょう。このタイプのグラフの他との大きな違いは、白丸と黒丸でグラフが寸断されることです。これは料金の数値のパターンが決まっていること、そして料金が常に整数となるため、例えばロウソクの長さと時間のような1本の直線で表されるグラフで見られる「連続性」がないことによります。

　グラフの成り立ちを整理する際には、「何回加算されるか」に着目します。最低料金の380円から問題の対象となる1160円までに、60円の加算が何回あるかを計算しますが、ここでは単純に1160円と380円の差額を60円で割ればよく、植木算のような間隔を考慮する必要はありません。

　(1160－380)÷60＝13（回）より、13回の加算となります。ここでポイントとなるのが、「最も高い料金を出すこと」です。グラフが同じ金額で文字数に幅が出るタイプですので、その幅のどの部分を出すかで迷ってしまいがちですが、計算で求めた加算数をそのまま使えば、最も大きな値（グラフの黒丸）になります。そして、最後に5字を「引き算」をすることで、白丸部分の文字数が求められます（この問題では何字以上何字以下を答えるので、1を足します）。

　もう1点注意したいのが、実際にグラフで示されている数値を使って、解法の確認をすることです。その際には扱いやすい数値として、500円のときの文字数を計算で求めてみて、それがグラフの通り、31字以上35字となれば、解法が正しいと確かめられます。

　解法を覚え込めていれば確実に得点源にできる問題ですので、くり返し解法を確認して、テストの際に迷わず解き進められるように、しっかり整理しておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。