メールマガジン宝箱 Mail magazine

5年10月度マンスリーテスト予想問題　現在無料公開中です！

　1つの攻略ポイントを20分でおさえられるように構成しています。しかも、昨日公開した予想問題と連動していますので相乗効果が得られます！旅人算・時計算といった速さの難問だけでなく、図形の移動もテスト範囲となる難問出題必至のマンスリーですが、5つのポイントを武器に持てば必ず勝てます！ 頑張ってください！！
予想問題はこちらのページで無料公開中です。

それではランキングの発表です。まずは第5位からです！

【第5位　図形の移動：円が多角形の頂点を通った後の線を正確に作図できていますか？】

　例えば、「1辺の長さが4cmの正六角形の外側を、半径1cm、中心Ｏの円がすべることなくころがります。このとき、中心Ｏのえがく線の長さを求めなさい。」といった問題。ポイントは正六角形の頂点を円が通過する際の、中心Ｏの動きです。
　ここでは辺に対して垂直な線を使うことがポイントです！中心Ｏが弧をえがくことまでは理解できても、その弧の中心と半径、そして何度分を動いたのかが曖昧になってはいないでしょうか。
　下の図のように、正六角形の辺に対して垂直な線を引くと、どこからどこまでが弧の動きになるのか、すぐにわかるのです。

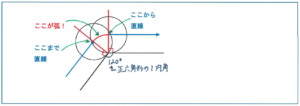
　弧を正確にかくことの重要性はこの後にも触れますが、弧が曖昧になってしまうと計算間違いが起こりやすく、失点の元になります。十分に注意しましょう。
　ちなみに上の問題では、弧の中心角がそれぞれ60度（360－90×2－120）になり、それが6カ所あることから弧を合計すると円周1つ分になります。よって、2×3.14＋4×6＝30.28より30.28cmが答えとなります。

【第4位　図形の移動：回転移動の点の動きを正確に作図できていますか？】

　図形の移動の中でも、直線上を多角形や円がすべることなく回転移動するパターンです。例えば「1辺の長さが3cmの正三角形ABCが直線上をすべらないように回転し、ふたたびBCが直線上にくるまでに、点Aが動いてえがく線の長さは何cmになりますか。」といった問題。
　下の図のように、正三角形を並べてかいて各点の位置を決めれば、長さを求めるのは難しくないでしょう。ポイントになるのは、弧となる線のかき方です。

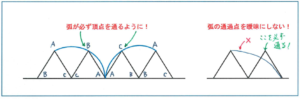
　ここでかかれる弧の半径はすべて正三角形ABCの1辺3cmですので、弧は必ず正三角形の頂点を通ることになります。右の図のように、本来通るべき点を弧が通過していないようなことがないように、徹底的に注意してください。この線のかき方を曖昧にしてしまっていると、問題の難度が上がった時に間違えてしまう可能性がとても高くなってしまうのです。細かいようですが、ここで基本をおろそかにしてしまうと、後になって取り返しがつかなくなってしまいます。
　上の問題の正解は、3×2×3.14×240/360＝4×3.14＝12.56より、12.56cmです。

【第3位　時計算：必ず起点となる時刻を図にしましょう！】

　時計算の演習では、速さが長さではなく角度で表されることに注意が必要です。角速度とも言われますが、その点に注意しておけば、あとは旅人算の考え方で解決できる問題がほとんどです。
　ただし、長針や短針の動きは図を用いるかどうかで、理解のしやすさに大きな違いが生まれます。少しでも解法に戸惑った際は、必ず図をかくようにしましょう。その際に、起点となる時刻もかくように気をつけてください。　
　例えば「4時から5時までの間で、時計の長針と短針の作る角度が1回目に45度になる時刻を求めなさい。」といった問題があるとします。

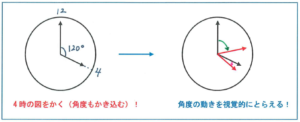
　ここで図をかく際に、「だいたい、4時○分くらいかな…」と当てをつけてかくのではなく、まず起点となる4時の図をかくことから始めましょう。そうすることで、長針と短針の間が何度縮まればよいのか、が視覚的に把握できる効果があります。このような作図の段階を踏んでおくことで、これから時計算の難度が上がった問題に対応する際に圧倒的な違いが生まれるのです。
　ちなみに上記の問題ですが、(30×4－45)÷(6－0.5)＝13・7/11より、4時13・7/11分が答えとなります。分数計算でミスをしないように気をつけましょう。

【第2位　旅人算（予定との時間の差）：予定よりも2分遅れる、を図にする！】

　旅人算の中でも頻出パターンのひとつが、次のようなタイプの問題です。
「太郎君は、乗る予定の電車の発車時刻に間に合うように、8時ちょうどに家を出発し、駅に向かいました。分速84mで進むと、発車時刻の5分後に駅に到着することがわかっていたため、分速120mで進み、発車時刻の2分30秒前に駅に到着しました。太郎君が乗る予定の電車の発車時刻は何時何分ですか。」
　このタイプの問題では、発車時刻の5分後に到着、2分30秒前に到着、といった時間をどのように扱うかが最大のポイントになります。そこで、時間を表す図をかいてみましょう。そこで注目するのが速さの違いです。距離が一定の場合、速さの比と時間の比は逆比の関係にあることはこの問題を解くうえで欠かせない要素なのですが、図をかき始める際には、むしろイメージを大事にした方がよいでしょう。
　分速84mで進むのと、分速120mで進むのでは、どちらがより時間がかかるか…もちろん遅く進む分速84mの方ですね。そのイメージをもとに、この時間の関係を図にしてみましょう。

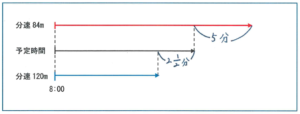
このように、「5分後（5分遅れ）、2分30秒前」を図にすることによって、ここから比を使って解く際にもより解きやすくなるでしょう。算数をイメージだけで解いてはいけませんが、図をかく際にはイメージを元にすることが大事です。
　この問題の答えですが、84：120＝7：10より、10－7の3が5分＋2分30秒＝7分30秒＝7・1/2分にあたります。分速84mで進んだ際にかかる時間が、7・1/2÷3×10＝25より25分となり、これでは発車時刻の5分後になってしまうので、8時＋25分－5分＝8時20分が求める答えとなります。
　このタイプの問題では、最後に何を求めるのか、にも十分注意しましょう。
　

【第1位　旅人算（まん中で出会う）：比を「見える化」できていますか？】

　今回のマンスリーでは、比を使って解くタイプの旅人算からの出題が予想されます。第2位の問題でも距離が一定の場合の、速さと時間の逆比の関係を使いました。そして、ここで取り上げる問題も比を使うのですが、ポイントは比をいかに「見える化」するか、という点です。
　次のような問題をどう解けばよいでしょうか。
「太郎君は12時に学校から公園に向って出発し、分速54mで進みます。花子さんは12時4分に公園から学校に向って出発し、分速72mで進みます。2人は学校と公園のちょうどまん中で出会いました。学校から公園までの距離は何mですか。」
　2人の進む速さがわかっていますので、その値をいかに利用するかを考えます。2人が進む時間が同じであれば、進む距離の比は速さの比と等しくなります。そこで、下のような図をかいてみましょう。
　その際に、同じ時刻を同じ記号で表すことに注意してください。

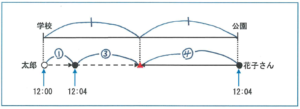
　ここでお子様に、太郎と花子の速さの比、54：72＝3：4がどの長さに相当するか聞いてみてください。上の図で、●～▲は同じ時間で太郎と花子が進んだ距離ですので、2人が●～▲で進んだ長さの比が3：4となることを答えられるかどうかがこの問題を解く鍵となります。速さの比を距離の比に換えて、図の中で見える化することで一気に正解に近づくことができるのです。
　この問題の正解ですが、太郎の○～●の距離が54×4＝216（m）、それが④－③＝①にあたります。学校から公園までの距離は④×2＝⑧ですので、216×8＝1728（m）が正解となります。　
今回は速さでの比の扱いによく気をつけて復習を進めてください。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。