メールマガジン宝箱 Mail magazine

　今回は比の中でも、面積図などの図を使って解くタイプの出題が予想され、図をうまく使いこなせるかどうかが結果を左右します！解説もよく読んで、図のかき方をがっちりマスターしましょう。ぜひ、偏差値アップ、クラスアップを実現してください。応援しています！
　さらに、このメルマガは明日公開の予想問題と連動しています。これから紹介する3つのポイントと予想問題で鬼に金棒です。予想問題はこちらのページで無料公開します！

【直前チェックポイント１：面積図を正確にかけていますか？】

　今回のテスト範囲のうち、「平均」「濃度の問題」では面積図が強力な武器となります！面積図を上手く活用できれば、問題内容を正確に整理することができ、正答率アップにつながるのです。
　例えば次のような平均の問題。　

　面積図の基本は、2つの要素とそのかけ算の結果、合わせて3つの要素を図にまとめて整理できることにあります。
　例えば平均であれば、（全体の和）÷（個数）＝（平均）となることから、（平均）×（個数）＝（全体の和）という式が成り立ちます。食塩水の濃度であれば、（食塩水の量）×（濃度）＝（食塩の量）となります。
　長方形の面積の公式が、（たての長さ）×（横の長さ）＝（面積）となることから、かけ算の結果を面積で表すことで、面積の大きさの関係からたての長さにあたる要素と、横の長さにあたる要素の関係を整理することができるのが面積図なのです。
　上の問題であれば、男子と女子の人数の比が7:6なので、男子の人数を⑦、女子の人数を⑥とおくと、男子のみの合計点は⑦×64、女子のみの合計点は⑥×77と表すことができます。
　そして、その2つを合計させたものが、クラス全体の点数の和、となります。
　ここまでが下の図です。

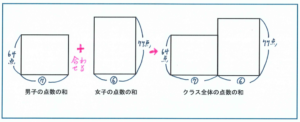
　ここまでで注意すべきは、あまり厳密に図をかこうとし過ぎないないことです。数値の大小関係がおおよそわかればよいのです。面積図は長さは面積を正確に求めるための図ではなく、式を立てるために量の関係を把握するための図なので、細かい数値まで正確にかく必要はないのです。
　さて、ここからが面積図作成のメインイベントです！じっくりと何を求めるかを確かめながら進んでいきましょう。

　上の段階でのクラス全体の点数の和は、2つの長方形の面積の和、つまりデコボコなかたちで表されています。これを、面積を変えずに1つの長方形のかたちにして、デコボコな図形の上に重ねます。
　クラス全体の点数の和は、（クラス全体の平均点）×（クラス全体の人数）で表されますので、クラス全体の平均点を□点、とすると、□×(⑦＋⑥)の式、面積では下の赤字で表される長方形になります。

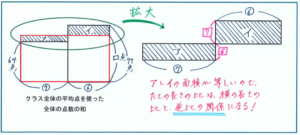
　上の右図がポイントです。長方形の面積が同じであれば、たての長さの比と、横の長さの比は逆比の関係にあることを利用します。
　左図のデコボコの図と赤の長方形が同じ面積ということは、左側（男子の合計得点）の長方形の赤線より下の部分と、右の長方形の赤線より上の部分が同じ面積になります。
　右図は、その同じ面積になる2つの部分を拡大したものです。アの長方形とイの長方形が同じ面積で、アの横線の長さとイの横線の長さの比が7:6であることから、たての長さの比は逆比の6:7になります。
このたての長さの比が正解に直結する大事な値ですので、図にしっかりかき込むようにしましょう。
あとは、77点と64点の差を7:6にわければたての長さが求まります。
(77－64)÷(7＋6)×6＝6（点）
64＋6＝70
より、クラス全体の平均点が70点となります。

　図さえかけてしまえば、あとは逆比の関係に気を付ければ、答えに至るまでの過程は決して複雑ではないのが面積図です。最初は時間がかかってもかき慣れてくれば、作成する時間は確実に縮まります。
　様々な場面で有効に活用できる強力な武器ですので、面積図のかき方をしっかり理解しましょう。

【直前チェックポイント２：食塩水の混ぜ合わせでも面積図が絶大な効果を発揮します！】

　チェックポイント1で挙げた平均の問題は、面積図を使わなくても、計算だけで解くこともできます
比の値をそのまま計算に使って、　
64×7＝448（点）→男子の合計得点
77×6＝462（点）→女子の合計得点
(448＋462)÷(7＋6)＝910＋13＝70（点）
として求めることもできるのです。

　それでは、次のような問題はどうでしょうか？

　食塩の量を求めようにも、食塩水の量がわからない。とり出した食塩水の量を推測で書き出しながら当てようとすると途方もない作業になってしまう…式だけで解こうとすると、なかなか手の打ちようがないところです。　
　そこで面積図をかいて解いてみましょう。
　詳しいかき方は割愛しますので、チェックポイント1 を参考にしてください。

　上の図のアとイの面積が等しく、濃度の差からアのたての長さは15－9＝6、イのたての長さは24－15＝9より、たての長さの比が6:9＝2:3となります。
　右の長方形と左の長方形の横の長さの比が2:3の逆比、3:2になることから、容器Ａからとり出して
混ぜた食塩水の重さは、
200÷(3＋2)×3＝120（ｇ）
と求まります。
　問題から得られる、式を立てるために必要な情報が少ない場合でも、面積図が使えれば解き進められるケースが多くあります。その点でも面積図は極めて有効なのです。

【直前チェックポイント３：倍数算で「差」が変わらない問題は、線分図の左側で増減を表す！】

　倍数算の中で、以下のような問題があります。

　倍数算では、どの量が変わっていないか、に注意しましょう。この問題では、2人ともに300円を使ったので、ノートを買う前と買った後で2人の所持金の差が変わらないことになります。
　ここで内容を整理するために線分図をかいてみるのですが、このような差が変わらない問題では、変化する量を線分図の左側で表すことに注意してください。
　どういう意味か、実際に線分図をかいてみましょう。
※メルマガでは○や□の中に数字を入れたかたちが文字化けしてしまうので、マル1、シカク2として表します。

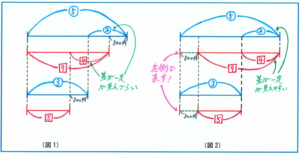
上記の（図1）では、兄と弟それぞれの線分図の右側から300円分を短くしています。この場合、差が一定であることが少し見えづらくなってしまいます。
そこで（図2）のように、300円分を左端から短くしてみると、差が一定であることがより明確になり、マル5－マル3＝マル2とシカク9－シカク5＝シカク4が等しくなることがわかりやすくなります。
あとは、
マル2＝シカク4よりマル1＝シカク2
ノートを買う前の兄と弟の所持金の比　→シカク10：シカク6
ノートを買った後の兄と弟の所持金の比→シカク9：シカク5
となることから、シカク1が300円に相当することがわかります。
よって、兄のはじめの所持金は、300×10＝3000（円）と求まります。

　線分図のかき方を一工夫することで、量の変化と、それによる比の変化が断然見やすくなることがあります。自分の手を使って図をかく練習を重ねることで、工夫の仕方も身についていきます。図をかく練習を怠らないように気をつけましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に100％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。