メールマガジン宝箱 Mail magazine

　ズバリ問題の偏差値アップのポイントは、図を活用して問題の内容を整理することです！例えば多くの生徒さんが苦手とする「長いす型の問題」。頭の中で問題内容をイメージしようとすると、なかなか式を立てられなくなってしまいます。そんな時に図を使って内容をまとめれば、人数の残り、いすの残りといった扱いづらい数値をスッキリと整理することができるのです。その他、通過算や相当算など、それぞれの問題に適した図の活用方法があります。それらをマスターすれば、今回のマンスリーでの得点力アップだけでなく、6年生になってから飛躍的に偏差値を上げる足場固めができます！
　ランキングでご紹介する5つのポイントをしっかりおさえて、偏差値アップ、クラスアップを実現してください。応援しています！

　さらに、このメルマガは明日公開の予想問題と連動しています。これから紹介するランキングと予想問題を照らし合わせればパーフェクトな仕上がりでテストに臨めます！頑張ってください！
予想問題はこちらのページで無料公開します！

【第5位　和と差に関する問題①：長いす型の問題で式を正確に立てられていますか？】

　和と差に関する問題の中で、以下のような長いす型の問題で式を立てるのに難しさを感じていないでしょうか。

といった問題。
　このタイプの問題の難しさは、基本的な過不足算のように、不足、あまりの数値が見つけづらいところにあります。そこで図でこの状況を整理してみましょう。

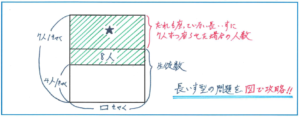
　図の★の部分は、7人ずつ座らせた場合にあと何人座れたのかを表しています。残った4きゃくにも7人ずつ座れば、7×4＝28（人）が座れますから、これが★の部分にあたります。図の斜線部分は28＋8＝36（人）なので、36÷(7－4)＝12より長いすの数が12きゃくとわかり、男子生徒数が4×12＋8＝56(人)と求められます。　
　図で的確に内容を整理する練習を重ねましょう。

【第4位　通過算：距離の差を問題から導き出せていますか？】

　通過算の中で、2つの異なる状況を使って解き進めるタイプの問題があります。例えば、

といった問題。解答の方針として、人を追い越した場合と自転車を追い越した場合を比べて、距離の差を求め、それを時間の差で割ることで路面電車の速さを求めます。速さがわかれば、通過算の基本から路面電車の長さは簡単に求めることができます。
　状況を図にすると、以下のようになります。

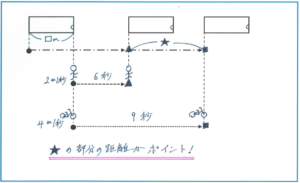
　ポイントは★の部分です。この距離を路面電車は9－6＝3（秒）で進んだことが図からわかります。★の部分の距離ですが、人の動きと自転車の動きに注目すれば、以下の式で求められます。
4×9＝36（m）…自転車が進んだ距離
2×6＝12（m）…人が進んだ距離
36－12＝24（m）★の部分の距離
24÷(9－6)＝8（m/秒）…路面電車の速さ
8×6－12＝36（m）…路面電車の長さ
　上記のように、式の大半は路面電車以外の2つの要素を使って作られています。求める内容（この問題であれば路面電車）以外の要素をいかに使うかに注意するようにしましょう。

【第3位　相当算：線分図をかく際には、数値が重なる部分に注意しましょう！】

　相当算の中で、全体に対する割合に人数などの数値を足したり引いたりして要素を説明するタイプの問題に解きづらさを感じられることが多くあります。線分図で問題内容を整理すれば解答の糸口が見つけられるのですが、図をかく際には慎重に取り組みましょう。以下の問題を例とします

　まず、クラス全体の生徒数を数値で表すのに2つの方法があります。「全体を1とする」パターンと、「全体を割合の分母の最小公倍数とする」のパターンです。予想問題の解説は前者としていますので、ここでは後者の最小公倍数を使う方法で進めます。
　4/9と3/5の分母、9と5の最小公倍数45から、クラス全体の生徒数をマル45とすると、めがねをかけている生徒数は、マル20＋6（人）、かけていない生徒数はマル27－8（人）となります。

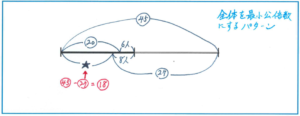
　図にそれぞれの数値を記入すると、★の部分はマル45－マル27＝マル18にあたりますので、8－6＝2（人）が、マル20－マル18＝マル2にあたります。よって、クラスの生徒数は2÷マル2×マル45＝45（人）と求められます。
　ここで、
(マル20＋6)＋(マル27－8)＝マル45
マル47－2＝マル45
マル1＝2÷(47－45)＝1より、
クラスの生徒数が1×45＝45（人）と求められますが、計算が少し複雑になりますので、図から解く方法も覚えておくとよいでしょう。

【第2位　和と差に関する問題：取り違える問題は面積図でも攻略できる！】

　和と差に関する問題の中で、2つの種類の商品を、予定していた個数を逆に取り違えてしまうタイプの問題があります。例えば次のような問題。

　まず、個数を取り違えた結果、代金が予定よりも高くなったので、予定では安い商品Ｑを多く買うはずであったことを確実にとらえておくようにしましょう。
　そこで状況を整理すると以下のようになります。

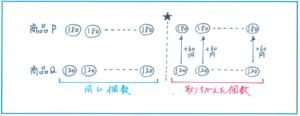
　取り違えた個数の1個あたりの金額の差が180－120＝60（円）なので、取り違えた結果、商品Ｐを商品Ｑよりも480÷60＝8（個）多く買ったことがわかります。予定では、商品Ｑを商品Ｐよりも8個多く買うはずでしたので、あとは和差算の考え方で、予定の商品Ｑの個数は(20＋8)÷2＝14（個）、Ｐの個数は20－14＝6（個）とわかりますので、予定の代金は180×6＋120×14＝2760（円）と求められます。
　まずはこのように図で問題内容を整理することをおすすめします。そのうえで、面積図を使う方法もご紹介しましょう。

　予定していた商品Ｐと商品Ｑの組み合わせを表す面積図から、ＰとＱの個数を逆にしたものを上下さかさまにして元の面積図の上に重なると、大きな長方形ができます。そのたての長さは180＋120＝300(円)、横の長さは20（個）なので、面積が300×20＝6000円となります。取り違えた結果、予定より480円高くなるので、上の部分の面積の和が、下の部分の面積の和よりも480円高いことになります。求めるのは、予定していた下の部分の面積ですので、和差算の考え方で(6000－480)÷2＝2760（円）となります。
　活用できる図が多いとテスト会場でより余裕をもって問題に向かうことができます。

【第1位　倍数算：和も差も変化する問題に対応できていますか？】

　倍数算の中でも、和が一定の問題、差が一体の問題は解法パターンが習得しやすいのですが、次のような和も差も変化するタイプの問題は式の進め方に注意が必要です。例えば以下のような問題。

　ここで問題内容をそのまま式にしていきましょう。
　はじめのＳさんとＲさんの所持金を、それぞれマル4円、マル1円とすると以下のような比例式が立てられます。
　(マル4－1000)：（マル1＋800）＝3：1
　ここで比例式の内項の積と外項の積が等しいことを利用すると、
　(マル4－1000)×1＝（マル1＋800）×3
　マル4－1000＝マル3＋2400…★
　ポイントはここからの式の進め方です。
　数学で移項の考え方を習われた親御さんはすぐに
　　マル4－マル3＝2400＋1000
　という式が立てられますが、小学生のお子様方は移項の考え方を習っていません。
　そこで、両辺に同じ作用をして等式の関係は崩れないことを利用しましょう。まずは★の式の両辺に1000を足すと、
マル4－1000＋1000＝マル3＋2400＋1000
マル4＝マル3＋3400
　と、式の左辺から数値を消すことができました。そして、両辺からマル3を引くことで、
　　マル4－マル3＝3400
　とすることができます。すぐに移項の考え方を教えてしまうのではなく、上記のような流れを説明しておくと、間違いを大きく減らすことができます。
　また、以下のように図で表すことも有効になります。

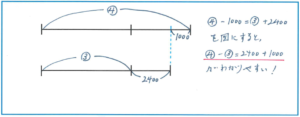
　すぐに等式を左右移動させると＋と－が変わると伝えるのではなく、式の性質や図を使うことで、より理解を強く固めるようにしましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。