メールマガジン宝箱 Mail magazine

　サピックス新6年生の皆様、今回の組分けテストで偏差値をアップさせるには、問題を見てすぐに的確な解法を選び出せるかどうかがポイントになります。これまで様々な算数の解法を学んできましたが、これからはそれを的確に使い分けられるかどうかが得点力の差に直結してきます。たとえば売買損益の問題に見えながら「つるかめ算の解法」を使う問題や、公約数が見つけづらい整数の問題など、ひとつの解き方にこだわってしまうと得点できない問題が増えてくるのがサピックスの新6年生です。
　解いた問題を見直す際に答え合せで終わらせずに、解法まで確認する習慣をつけておきましょう。そうして解法を増やしておけば、差がつく問題で確実に得点することができるようになります！
　ランキングでご紹介する5つのポイントをしっかりおさえて、偏差値アップ、クラスアップを実現してください。応援しています！
　さらに、このメルマガは明日公開の予想問題と連動しています。これから紹介するランキングと予想問題を照らし合わせれば組分けテストでの偏差値をこれまでにないレベルにまでアップさせられます！頑張ってください！
予想問題はこちらのページで無料公開します！

【第5位　おうぎ形の相似：比を用いた面積の求め方もマスターできていますか？】

　三角形や四角形の相似の関係は見つけられても、おうぎ形にも相似の関係があることに気づかず、それを利用した解き方を活用できていないケースがよく見られます。中心角が同じおうぎ形はすべて相似の関係にあり、それを利用して比を用いた解き方ができます。
　下の図のように、正三角形の周りにおうぎ形ができるタイプの問題を例にしてみましょう。

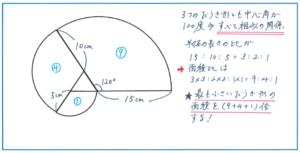
　上の図の3つのおうぎ形はどれも中心角が180－60＝120（度）となるので相似の関係にあります。ここでそれぞれの半径が15cm、10cm、5cmですので、(15×15＋10×10＋5×5)×3.14×120/360として計算することも、もちろんできます（予想問題ではこの解法で進めています）。比を使った解法が思いつかない場合は、すぐにこちらの解法で計算を進めましょう。ここで比を使う場合には、おうぎ形の面積比を用います。半径の長さの比が15：10：5＝3：2：1なので、面積比は3×3：2×2：1×1＝9：4：1となります。あとは面積比1にあたる最も小さいおうぎ形の面積を、9＋4＋1＝14（倍）すれば答えに行き着けます。5×5×3.14×120/360×14の式で答えを求めることができるのです。
　計算の手間に大きな差はありませんが、解法の幅を持っておくと、自分の使いやすい方法で進めることで、計算ミスを減らせる効果があります。ぜひどちらの解法も試してみてください。

【第4位　数の性質：数の差から公約数を求める方法を使えていますか？】

　数の性質の問題などで2つの整数の公約数を求める必要がある際に、どちらの整数も一見約数が見つけづらいことがあります。例えば、「187と221の最大公約数を求める」といった場合、どちらの整数も奇数であり、3でも5でも割ることができないため、すだれ算で進めようとしても手が止まってしまいます。

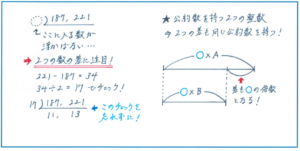
　こうした場合は、2つの整数の差に注目してみましょう。上の右の線分図で表されるように、公約数を持つ2つの整数の差もその公約数の倍数になります。
　221－187＝34より、2つの数の最大公約数は34の約数となります。221も187も奇数のため、偶数である34は公約数には該当しません。そこで34÷2＝1をすだれ算でチェックしてみると、221＝17×13、187÷17＝11と、17が最大公約数であることが確定できます。
　6年生になるとテストで使われる数値も複雑になることが予想されます。その最大公約数や最小公倍数を求める際に、どれだけ時間を短縮し、正確に進めるかがテスト全体の偏差値にも大きく影響してきます。数そのものだけでなく、その差にも着目する習慣を早めに身につけておきましょう。

【第3位　立体図形：見えない部分の面積を逃さないために段ごとに考える解き方があります！】

　立体図形で表面積を求める際に、表面から見えない、陰になっている部分をどのように求めるのかがテストで得点差をつけるポイントになります。
　下の図は、1辺が1cmの立方体を64個合わせた立方体で、斜線部分3か所から、それぞれ反対側まで並んでいる立方体をすべて取り除いてできた立体図形です。この表面積を求める場合、くり抜いた立体について別に考える方法もありますが、ここでは立体を段ごとに区切って考える方法をご紹介します。

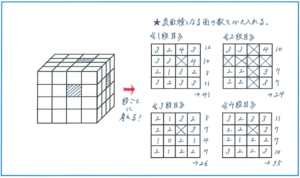
　右の4つの平面は、それぞれ立体を1段目から4段目までに分けたもので、それぞれの正方形の中に、表面積として数えられる面の数をかき込んだものです。注意すべきは3か所でくり抜かれた部分で、特に1段目では下の部分に、3段目には上の部分に表面積に数えられる面がある点です。そこを慎重に取り組めば、少し時間はかかりますが、くり抜いた立体の図形を間違えてしまうようなリスクは避けられます。上記の問題では、41＋24＋26＋35＝126より、表面積が126平方cmと求められます。小さな立方体を組み合わせて大きな立体とするパターンでは、このような数え上げの方法が使えますので、ぜひ試してみてください。

【第2位　つるかめ算：別の単元に見える問題で、つるかめ算を利用できていますか？】

　一見すると別の単元の問題のようで、最終的にはつるかめ算を使って解くタイプの問題が、テストで出されることが多くあります。そのような問題に対した際に、迷わずつるかめ算が使えるかどうかで、正解に至るまでのスピードに大きな差が生まれます。例えば次のような問題。

　この問題では仕入れ値、定価、利益を扱いますので、もちろん売買損益の基本的な考え方は使うことになります。ただ、最後に求める定価で販売したペンの本数は、つるかめ算で求めることになるのです。

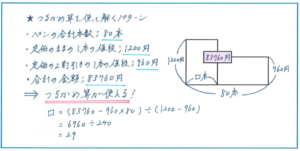
　こうしたつるかめ算が混入するタイプの問題に対応するには、まずは問題の内容にそって解き始めることが大事です。上記の問題であれば、売買損益の考え方で、ペンの定価、2割引きした価格を計算して、問題用紙のスペースに上の図の左に記したように、数値を書き出してみるとよいでしょう。そこで、2つの要素の単価と、合計の個数（この問題であれば本数）、合計金額がすべてわかっていることから、つるかめ算を使えるという方針に到達できます。後はつるかめ算で使う式で、(83760－960×80)÷(1200－960)＝6960÷240＝29より、答えを29本と求めることができます。つるかめ算では上の右の図のように面積図を使えることも見直しておきましょう。
　つるかめ算は速さでも用いることのある重要な考え方です。どのようなパターンであればつるかめ算を使えるのかが問題を見てすぐに頭に浮かんでくるように、つるかめ算の基本パターンをよく復習しておくとよいでしょ

【第1位　場合の数：組合せと順列の両方が必要なタイプの問題に対応できていますか？】

　多くの受験生が苦手とする場合の数。今回の組分けテストでも場合の数からも出題される可能性はとても高いと言えます。
　場合の数の中でも、組合せと順列の両方の解き方を用いなければならない問題には注意が必要です。
　例えば次のような問題に正確に対応できていますでしょうか。　

　まず和が6になる場合のサイコロの目の出方の組み合わせは（1、2、3）（1、1、4）（2、2、2）の3つで、出た目の順番として、（1、2、3）は3×2×1＝6（通り）、（1、1、4）は1つだけ異なる目の4が何回目で出るかの3通り、（2、2、2）は1通りと求められます。
　6の倍数はこの他に12と18があり、出た目の数が12、18となる場合は、それぞれ上の図のように整理でき、答えは6＋3＋1＋6＋6＋3＋6＋1＋3＋1＝36（通り）となります。
　問題としては決して難しくありませんが、場合の数の他の問題のように、数えもれに十分に注意し、3×2×1のように式で求められるものと、かき出して求めるものとを組み合わせて解き進めなくてはいけません。そのためには、かき出しをていねいに見やすくすることが重要です。当たり前のように思われるかもしれませんが、見やすくかき出していなかったために、得点源にできる問題で失点してしまうケースがとても多く見られます。美しくかく必要はありませんが、自分で見て内容が正確に把握できるようにかき出す必要があります。対策としては、普段の演習でノートにかき出したものを、時間を置いて見直してみるとよいでしょう。そこで自分のかき方を冷静に見ることで、つい見づらくかいてしまう数字がないか、乱雑にかき並べてしまって整理ができなくなっていないか、などが把握できる効果があります。そこで気づいた点を修正すれば、テストで見やすくかき出せるようになります。地道な作業にはなりますが、テストの得点力を高く安定させるためにも、かき出しの練習はぜひ重ねておくようにしましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。