メールマガジン宝箱 Mail magazine

　今回のテストでの偏差値アップのポイントは、立体図形の問題を解く際に、平面図形の性質を利用した解法を使いこなすことです。今回テスト範囲となる立体図形は、立体の切断や立体の表面に色を塗る問題、そして円すいの表面積に関する問題など様々なタイプが該当します。例えば円すいの表面積であれば、側面積の展開図であるおうぎ形のかたちを利用するなど、平面図形の問題を解く際の解法パターンを定着させることができれば、得点を大幅にアップさせることができます！テストは中止になる予定ですが、入試問題でも難問が多い立体図形について、すでに習った平面図形の考え方の利用方法をしっかり覚えておくことは、立体図形の分野での高得点獲得につながります！
　ランキングでご紹介する5つのポイントをしっかりおさえて、偏差値アップを実現してください。応援しています！
　さらに、このメルマガは明日公開の予想問題と連動しています。これから紹介する5つのポイントと予想問題を合わせれば得点力をかつてないほどにアップさせることができます！
予想問題はこちらのページで無料公開します！

【第5位　立体図形：表面を塗る問題は段ごとにわけて考えるとわかりやすいです！】

　立体図形で、例えば下の図のような1辺5cmの立方体のすべての表面を赤くぬり、その立方体を1辺1cmの立方体125個に切り分けた場合、1辺1cmの立方体を、面がいくつぬられているかというケースを考えてみます。

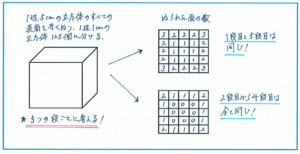
　このタイプの問題は慣れてくれば、1辺1cmの立方体で赤くぬられた面の数が、3つ、2つ、1つ、そして0に分かれることが容易にイメージできるようになりますが、慣れないうちは、上の右の図のように、立方体を上から5つの段に分けて、段ごとにぬられた様子を把握するとわかりやすくなります。特に気をつけて頂きたいのが、赤くぬられる面の数が、上から1段目と5段目は同じ、2段目から4段目までも同じになることです。
　この立体を段に分けて考える方法が習得できていれば、例えば立体に穴を通した形の表面積を求める際に活用することができます。平面図形に比べてイメージがしづらい立体図形ですので、少しでも自分がイメージしやすいかたちに立体を加工する練習をしておけば、立体図形の単元での得点力が大きくアップします。

【第4位　2量の関係：タクシー料金型の問題をグラフや図を使って対応できていますか？】

　2量の関係の単元のうち、タクシー料金や運賃のタイプの2量の変化についての問題は、幅がある答えを求めさせることもあり、苦手とされる生徒さんが多く見られます。例えば、次のような問題です。

　このタイプの問題では、下の図の左にあるようなグラフを使って解くことができます。このグラフを自分でかく際には、段差が見えやすいようにグラフの線に間隔をあけることと、数値を含むことを表す●と、含まない〇を使い分けられるように注意しましょう。

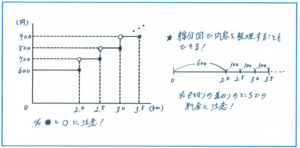
　あとはグラフを見ながら式を立てていきます。11.6kmのうち2kmを超えるのは、11.6－2＝9.6(km)あり、9.6÷0.5＝19あまり0.1より、加算される回数が19＋1＝20（回）とわかります。よって料金が、600＋100×20＝2600（円）と求められます。
　ここで式について注意すべき点が2つあります。まずは、商として求められた19は加算の回数ではなく、1を加えなくてはいけないことです。その点の理解が曖昧な場合は、グラフを見て求められる小さい数でチェックをするとよいでしょう。例えば、3.2kmを走った場合の料金は、3.2－2＝1.2、1.2÷0.5＝2あまり0.2まで求めます。そこでグラフの横軸の3.2kmの位置から上にたどると、料金は600円に100×3＝300（円）を加算した900円であることがわかります。ここから、加算の回数が計算結果に1を加えたものであることが確認できます。このように式の答えをそのまま使ってよいかどうかを、数を小さくすることで確認する作業は、他の単元でも使えますので、覚えておきましょう。
　注意すべきもう1点は、9.6÷0.5＝19.2といった計算をしてしまわないことです。ここでは加算の回数を求めるので、必要なのは商の整数部分のみです。求めるものが何かによって計算をどこまで進めるかが変わってきますので、慎重に対応しましょう。
　上の左のグラフは、グラフの問題への対応力を鍛えるためにはぜひかく練習をして頂きたいですが、より簡潔に解き進めるうえでは、右のような線分図で内容を整理することもできます。その場合には、〇や●が使えない分、区切りにあたる部分では料金がいくらになるのかに気をつけてください。例えば2.5kmでは、料金は800円ではなく700円となります。図を慎重に見る習慣を身につけましょう。

【第3位　立体図形：円すいの側面積上の線の問題は、展開図で考えましょう！】

　今回のマンスリーの立体図形では、円すいの性質を使った問題が出される可能性が高くあります。例えば次のような問題にはどのように対応すればよいでしょうか。

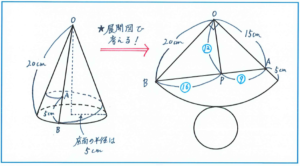
　こうした円すいの側面を通る線が最短になる場合についての問題では、円すいの側面の展開図を通る直線を利用して考えます。
　まずは円すいの展開図がどのようなかたちになるか考えてみましょう。円すいの側面の展開図は母線の長さを半径とするおうぎ形で、その中心角は、底面の半径／母線の長さとなることは基本的な知識としておさえておきましょう。この円すいでは、母線の長さが20cm、底面の半径の長さが5cmなので、展開図のおうぎ形の中心角は、360×5/20＝90（度）となります。
　求める長さは、右の展開図のABの長さになります。直角三角形の3辺の長さの比で、3：4：5となる図形があることを考えると、ABの長さは15×5/3＝25よりABの長さは25cmと求められますが、ここでは比を使った解き方で進めてみましょう。
　O（オー）からABに垂直な線OPをひくと、三角形ABO、三角形AOP、三角形OBPはどれも相似な関係にあり、AP：OP＝OP：BP＝15：20＝3：4となります。ここで、OPの長さをマル12とすると、APはマル9、BP＝マル16となり、ABの長さはマル25と表されます。三角形ABOの面積は15×20÷2＝150（平方cm）なので、マル25×マル12÷2＝マル150より、マル1＝1cmから、マル25で表されるABの長さが25cmと求められます。
　円すいの側面を通る線の最短の長さを求めるには、展開図のおうぎ形を通る直線から解き進めることに十分に注意しましょう。

【第2位　2量の関係：遅れたり進んだりする時計の問題は比で攻略しましょう！】

　正しい時刻を表示しないことを題材とする問題では、2つの点に注意が必要です。1点は比を有効に活用すること、もう1点は時間の計算を正確に行うことです。次のような問題を例にしてみましょう。

　まずは2つの時計がかかる時間を比で表すのですが、1時間あたりにずれる時間がわかっているので、正確の時間で1時間の間に2つの時計が進む時間で比べます。60分で時計Aは58分、Bは65分進みますので、2つの時計の進む比は、58：65です。この比が求められれば、正解に大きく近づいたと言えます。比を正確に求めることに集中しましょう。
　ここからは時間の計算に気をつけながら解き進めます。Aが午後9時46分までに、6時間46分＝406分進んだとき、Bは、58：65＝406：□より、□＝65×406÷58＝455分＝7時間35分進み、時計B の指している時間は、午後10時35分 とわかります。
　時間の計算はこれまでにテストの計算問題でも何度か演習してきています。この時計の問題では時間の計算を正確にできるかどうかが得点の分かれ道になりますので、時間の計算の正答率が低い場合は、何度でも練習しておきましょう。

【第1位　立体図形：立方体の切断面で正方形とひし形は正確に区別できていますか？】

　立体図形の切断の問題は、以前までは出題する学校が上位に限られていましたが、現在では偏差値を問わず出題されますので、解法を確実におさえておきたいところです。
　サピックスでは立体の切断を繰り返し演習しているので、切断線を引くところまでは正確にできているケースが多いと思われます。向かい合った平面上の線が平行になることなど、切断線の基本的な引き方が曖昧な場合はテキストで繰り返し練習をしておきましょう。
　ここでは、特に切り口のかたちを判断するうえで特に混乱しやすい、正方形とひし形の区別について確認します。下の図のような立方体で、辺BFの真ん中の点を点Pとして、点A、点G、点Pの3つの点を通る平面で2つに切り分けたときの切り口の形を考えます。

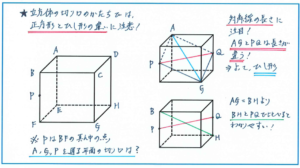
　まず切り口の形を確かめるために、どのような切断線になるかを正確に把握しておきます。平面ABFEと平面DCGHが平行になりますので、平面DCGH上にAPと平行な線が入ることになります。PがBFの真ん中の点ですので、DHの真ん中の点をQとするとGQがAPと平行な関係になります。ここで切り口のかたちは四角形APGQとわかりますが、この四角形について、AP＝PG＝GQ＝QAから正方形と間違えてしまいがちです。四角形の性質から4辺の長さが等しいのは正方形だけでなく、ひし形もあてはまります。正方形とひし形の違いをすぐに答えられるでしょうか。4つの角度がいずれも直角になれば正方形、向かい合う角度が等しいだけであればひし形ですが、この切り口の図形からは角度の関係がなかなかわかりづらくなります。そこで、もう一つの違いである対角線の長さに注目します。対角線の長さが等しければ正方形、等しくなければひし形になります。切り口の四角形APGQの対角線AGとPQを比べると、AGの方が長くなります。この長さの関係がわかりづらい場合は、AGをBHに置き換えてみましょう。どちらも立方体の向かい合う頂点を結んでいるので、AGとBHは同じ長さになります。四角形BFHD上で比べると長さの違いがわかりやすくなるでしょう。ここで四角形APGQがひし形になることがわかります。
　立体の切断の問題ではまずは立方体の切断で、切り口の図形を区別をパターンとして覚えておくことが大事になります。その際には、見た感じで図形を判断するのではなく、辺の長さや対角線の長さをしっかりと見て、根拠をもって図形を判断するようにしましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名くだ