メールマガジン宝箱 Mail magazine

　8月の夏期マンスリーテストは範囲がない実力テストです。これまで培ってきた力、夏休みの頑張りをテストにぶつけてクラスアップにつなげたいところです。そのためにも復習ポイントを正確に見出すことが不可欠になります。
　そこで、対策ポイントを、プロ家庭教師の視点から第5位から第1位までのランキングのかたちにまとめました。ぜひ偏差値アップ、クラスアップを実現してください！応援しています！
さらに、このランキングは明日公開の予想問題と連動していますので、予想問題も併せてご活用ください！
予想問題はこちらのページで1週間限定で無料公開します！

【第5位　分数計算：式のかたちをよく見て、解法パターンを間違わないようにしましょう！】

　大問1の計算問題の中で、分数計算で以下のようなパターンの出題があった際には要注意です。

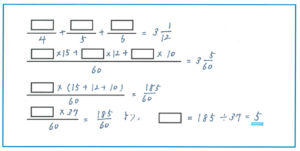
　分数計算の応用型では、次のような「分母に注目して1つの分数を2つの分数の差に変える」ケースがあります。

　よく分数を見て、そのケースがあてはまるかどうかをチェックする必要があります。式をよく見るとこの問題では、式の答えを出すのではなく、四角にあてはまる数を求めるので、2つの分数の差に変えるパターンではないことがわかります。
　そこでこの問題では、四角はそのままに、普通の分数計算と同じく通分をして計算を進めていきます。
　あとは計算ミスをしないように、特に分子に数をかけ忘れないように、正解にまで行き着きましょう。
　式のかたちに注意して、確実に得点してください。

【第4位　図形の移動：図形の重なりがなくなる時点を正確に求められますか？】

　図形の移動の問題の中で、2つの図形が重なっている時間を求める場合には、図形の重なりがなくなる時点に気をつけて解き進めましょう。基本的な考え方は速さの通過算と同じです。例えば次のような問題を正確に解けるでしょうか。

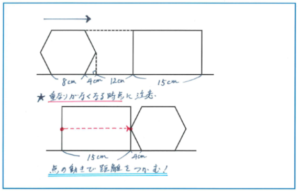
　この問題では下の図のような、正六角形の左端の頂点が長方形の右端の辺上にある時点で、2つの図形の重なりがなくなります。2つの図形が移動する場合は通過算の考え方と同じで、2つの図形の間にできる距離を速さの差で割ればよいですが、この問題では長方形は動きませんので、正六角形の動きのみに注目すればよいことになります。
　正六角形の右端の頂点が長方形の左端の辺上にある時点までの移動距離が12cm、そこからは正六角形の左端の頂点の動きに切り替えて、正六角形の向かい合う頂点を結んだ対角線の長さである4＋8＋4＝16（cm）、正六角形の左端の頂点が長方形の内部を移動する長さである15cmを加えます。合計して12＋16＋15＝43（cm）を移動しますので、求める時間は43÷2＝21.5（秒後）となります。
　速さの問題としては簡単ですが、問題によっては図形のかたちが複雑になります。長さを取り違えないように注意しましょう。

【第3位　食塩水の濃度：混ぜ合わせの問題で、面積図を使わずに解く方法を使えていますか？】

　食塩水の混ぜ合わせの問題では、面積図や天びん図を活用することが有効なケースが多いですが、速く正確に答えを求めることができますが、問題によっては図を使わずに計算で解き進める方が速く正確に正解に行き着くことができます。
　次のような問題です。

　この問題を、面積図を使って解くとすると、下の左のように図を2つかくことになります。図のかき方に慣れていれば、時間が余計にかかることはありませんが、制限時間のあるテストでは、よりスムーズに解き進めたいところです。

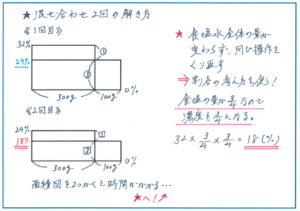
　そこで、割合の基本的な考え方を使って解く方針で考えてみましょう。
　食塩水400ｇに対して、100gは1/4にあたりますので、その100gの食塩水に含まれる食塩の量も全体の1/4になります。そこで1回の操作では食塩の量は1－1/4＝3/4になります。ここでポイントは、取り出した食塩水と同じ量の水を加えているので、食塩水全体の量は400gで変わらないことです。そのため食塩の量が3/4になれば濃度も3/4になります。この操作を2回繰り返すので、食塩水の濃度は、32×3/4×3/4＝18（％）となります。
　食塩水の混ぜ合わせであれば図を使う、と決めつけずに、解法を増やして問題に合ったものを活用することを心がけていきましょう。

【第2位　流水算：船のエンジンがとまった状況を正確に把握できていますか？】

　流水算の応用問題では、流速や船の静水時の速さが上りと下りで変化するパターンをはじめ、様々な出題パターンがあります。その中でも以下のようなエンジンが途中で停止してしまうパターンで状況を正確に把握することが難しい際には、図を使って視覚的にイメージをつかむとよいでしょう。
　例えば次のような問題です。

　この状況を線分図で整理してみましょう。下の図のようになります。

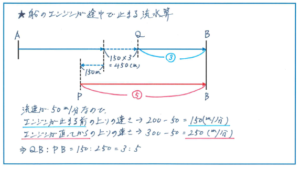
　まず注意すべきは、エンジンが故障した時点から船が下流に流される速さが流速と同じであること。そこで、この問題では流速を150÷3＝50（ｍ/分）と求められます。
　ここからがこの問題のポイントですが、エンジンが直ってから船の静水時の速さが変わることから、同じ時間にそれぞれの速さで進んだ距離を線分図から読み取りましょう。
　エンジンが直った地点をＰ、そしてエンジンが故障しないままに船が3分間進んだ場合の到達地点をＱとすると、分速150（200－50）ｍでＱからＢまで進むのにかかった時間と、分速250（300－50）ｍでＰからＢまで進むのにかかった時間が同じになります。よって、ＱからＢまでの距離：ＰからＢまでの距離＝150：250＝3：5となります。この距離の差が150＋450＝600（ｍ）となるので、ＱからＢまでの距離は600÷(5－3)×3＝900（ｍ）となり、求める距離は900＋450＝1350（ｍ）となります。
　流水算ではいくつもの種類の速さが出てきますが、図で整理することでそれらの速さをいかに使って問題を解くかが見えてきます。状況を表す図をかく練習を重ねましょう。

【第1位　ダイヤグラム：往復運動では追い越しとすれ違いの読み取りに注意しましょう！】

　速さの問題で往復運動をダイヤグラムに表すタイプの問題があります。そこでダイヤグラムに表された2つの対象の動きから、それぞれがすれ違う回数や追い越す回数を求める際には、グラフのかたちに十分に注意しましょう。
　例えば、バスＡが停留所ＰとＱの間を往復する間に、自転車Ｂが休憩なしでＱとＰの間を往復する様子を下のダイヤグラムのように表した場合について考えます。

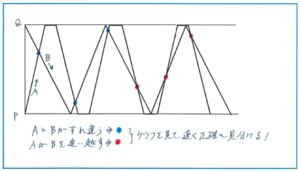
　上のダイヤグラムに記入した通り、落ち着いて考えれば、同じように交わる直線でも向きを考えればどちらがすれ違いで、どちらが追い越しが見極められます。ただ制限時間のあるテストでは、つい焦ってしまい、追い越しとすれ違いを混合して間違えてしまうケースが多く見られます。サピックスのマンスリーでは、こうしたタイプの問題は大問に含まれる小問として出題されます。とらえ違いのミスはその問題での失点だけでなく、他の小問の得点のチャンスを失うことにつながります。時間がない中でもミスをしないように、グラフの形状を普段から正確にとらえるように注意しましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。