メールマガジン宝箱 Mail magazine

　今回の組分けテストは範囲なしの実力テストです。これまで学習してきた内容で、どこを重点的に演習する必要があるのかチェックする必要があります。そこで、ぜひ気をつけて頂きたいポイントを、プロ家庭教師の視点から6年生、5年生ともに第5位から第1位までのランキングのかたちにまとめました。メルマガを読んで、ぜひ偏差値アップ、クラスアップを実現してください！応援しています！
　さらに、このメルマガの6年生のランキングは明日公開の予想問題と連動しています。ランキングで紹介する対策ポイントと予想問題を合わせれば、偏差値アップを一気にたぐりよせることができます！頑張りましょう！
予想問題はこちらのページで無料公開します！

≪6年　第4回組分けテスト≫

【第5位　規則性：分数が約分できないことの意味をしっかり理解できていますか？】

　規則性の問題では、書き出して決まりを見つけることも重要な手筋の1つです。問題文を読んでもわからないときは、手を動かして書き出してみましょう。

　2021を素因数分解すると 43×47 となります。43と47はどちらも素数なので来年度の受験のために、「2021＝43×47」は覚えておくとよいでしょう。
　分子が43でも47でも割り切れない数のときに、既約分数になります。
　 2020÷43＝46余り42 …… 43の倍数は46個
　 2020÷47＝42余り46 …… 47の倍数は42個
　ベン図にまとめると(図1)のようになります。

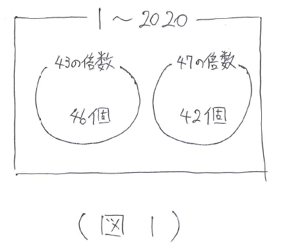
　したがって、約分可能な分数は 46＋42＝88(個) とわかります。よって、既約分数の個数は 2020－88＝1932(個) と求まります。
　また、既約分数を書き出すと(図2)のようになります。

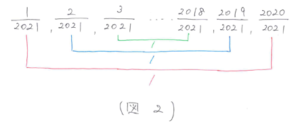
1/2021＋2020/2021＝1、2/2021＋2019/2021＝1、……となり、1が1932÷2＝966(組)できることがわかります。したがって既約分数の和は、1×966＝966 と求まります。

【第4位　立体図形：正方形のかたちをした三角すいの展開図の見方がポイントです！】

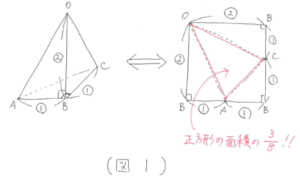
　立体図形の問題でよく出題される図形に、「体積と表面積のどちらも計算できる三角すい(図1)」があります。体積はともかく表面積はこの図形だと気づかないと解けないので注意しましょう。

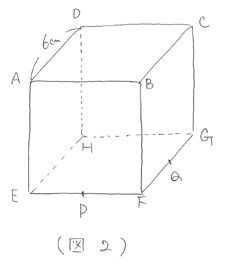
　はじめに切り口を作ります。上の面と下の面は平行になっているので、上の面の切り口の線と下の面の切り口の線も平行になります。頂点Aを通ってPQに平行になるように切り口の線を作るとACになります。このことから求める体積は三角すい台PFQ－ABC、求める面積は四角形APQCとわかります。
　次に、APの延長線とBFの延長線とCQの延長線が交わる点をRとすると(図3)のようになります。

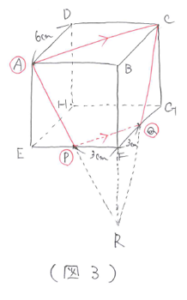
 ここで、三角すいR－ABCの展開図をかくと(図4)になります。

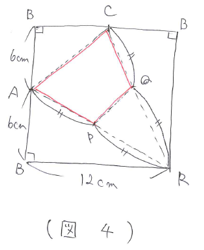
  三角すいR－ABCと三角すいR－PFQは相似比が2：1になっているので、体積比は
(2×2×2)：(1×1×1)＝8：1となります。したがって、三角すい台PFQ－ABCの体積は、6×6×1/2×12×1/3×7/8＝63(立方cm)と求まります。
△ACRと△PQRは 2：1 の相似になっているので、面積比は (2×2)：(1×1)＝4：1 となります。したがって、四角形APQCの面積は 12×12×3/8×3/4＝40.5(平方cm)と求まります。

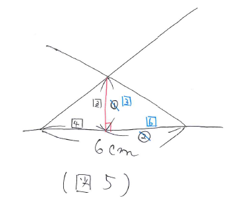
【第3位　文章題：線分図に記号化した数をかき入れると内容が整理できます。】

という問題を考えてみましょう。
　まずは問題文を図にまとめます。

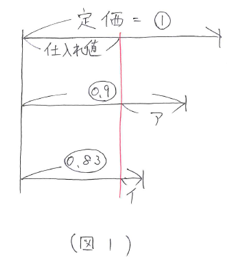
　定価をマル1、1割引きで売ったときの１個当たりの利益をア、1割7分引きで売ったときの1個当たりの利益をイとして図にまとめると(図1)のようになります。

また、問題文から ア×3＝イ×10 とわかるので　ア：イ＝1/3：1/10＝10：3 となります。新しくわかったことを図にかきこむと(図2)のようになります。

　
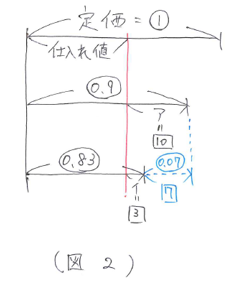
このことから、マル0.07＝シカク7 となり、マル1＝シカク100 とわかります。仕入れ値はシカク100×0.9－シカク10＝シカク80 となります。よって100÷80＝1.25、1.25－1＝0.25→2割5分 と求まります。

【第2位　速さ：時間と速さの逆比の関係を使って式を立ててみましょう！】

　次の問題を考えてみましょう。

　問題文を読むと、行きの方が帰りよりも時間がかかっているので、行きのときに上りが多いことがわかります。(図1)

　A町から峠までを考えます。行きと帰りの速さの比は 行き：帰り＝3：6＝1：2 なので、かかった時間の比は 行き：帰り＝2：1とわかります。峠からB町までのときも同じように考えて、速さの比は 行き：帰り＝2：1　、時間の比は 行き：帰り＝1：2 とわかります。
　このことから、
　　　行き：　マル2＋シカク1＝160(分)
　　　帰り：　マル1＋シカク2＝140(分)
となるので、消去算を使って解くと、マル1＝60(分)、シカク1＝40(分)とわかります。
　したがって、A町からB町までの道のりは、3×120/60＋6×40/60=10(km)と求まります。

【第1位　平面図形：補助線をひいて比の関係を整理できていますか？】

という問題を解いてみましょう。

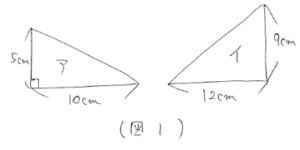
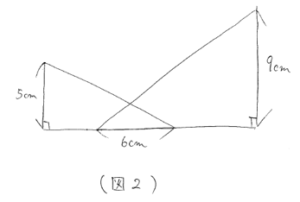
　補助線を引くとピラミッド型の相似ができます。直角三角形アの底辺と高さの比は、10：5＝2：1 なので、これに注意して図に比をかき込むと(図3)のようになります。

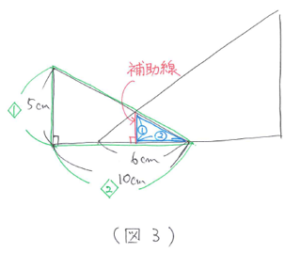
　直角三角形イでも同じように考えます。底辺と高さの比が 12：9＝4：3 に注意して図に比をかき込むと(図4)のようになります。

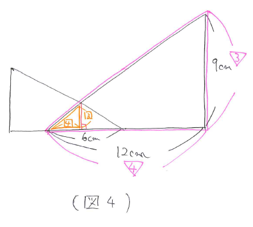
(図3)と(図4)で補助線を引いた部分の長さが等しいので、比をそろえると(図5)のようになります。

シカク10＝6(cm)、シカク1＝0.6(cm)、シカク3＝1.8(cm)となるので、重なっている部分の面積は 6×1.8÷2＝5.4(平方cm)と求まります。

≪5年　第5回組分けテスト≫

【第5位　立体図形：円すいの側面積の求め方を覚えられていますか？】

　予習シリーズ5年上の第11回で学習した内容です。角柱の体積や表面積の求め方、円すいに関する各公式、回転体の図のかき方などを中心に勉強していきましょう。次の問題を使って円すいの公式を確認してみましょう。

　底面の半径を□cmとします。円すいの側面積を求める公式は「母線×底面の半径×円周率」ですから、式を作ると17×□×3.14＋□×□×3.14＝628となり、□×(17＋□)×3.14＝628、□×(17＋□)＝200と整理できます。積が200になる整数の組は(1，200)、(2，100)、(4，50)、(5，40)、(8，25)、(10，20)と調べられ、このうち差が17になる組は(8，25)と分かります。したがって□＝8となります。
　体積の公式は「底面積×高さ×1/3」ですから、8×8×3.14×15×1/3＝320×3.14＝1004.8(立方cm)と求まります。
　円周率が絡む問題では、計算処理の仕方で難易度が大きく変化します。円周率はまとめて計算することを心掛けましょう。

【第4位　数に関する問題：商が整数でなくなるという意味を理解できていますか？】　

　予習シリーズ5年上の第1回や第14回で学習した内容です。倍数や約数、素因数分解などの基本事項の確認と、典型的な問題の練習を中心に勉強していきましょう。

という問題を考えてみましょう。
　Aを素因数分解したときに3が何個あるのかを考えます。
　200÷3　　　　　 ＝66余り2
　200÷(3×3)　　　＝22余り2
　200÷(3×3×3)　 ＝7余り11
　200÷(3×3×3×3)＝2余り39
66＋22＋7＋2＝97(個)
3が97個あるので、商が整数でなくなるのは 97＋1＝98(回目)と求まります。
　この問題のように、多少数字が大きくなっても解き方に違いはありません。最後まで解き切る計算力も一緒に養いましょう。

【第3位　割合の文章題：割合を普通の数字のように計算する方法を覚えましょう！】

　予習シリーズ5年上の第4回、第7回、第8回で学習した内容です。第4回では相当算、第7回では食塩水、第8回では売買損益を学習しました。必修例題や基本問題は復習して確実にできるようにしておきましょう。今回はこの中から相当算の応用問題を取り上げます。

という問題を考えてみます。
　まず、問題文を線分図に整理すると(図1)のようになります。

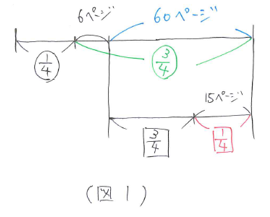
　これを計算すると、15÷1/4＝60、(6＋60)÷3/4＝88(ページ)と求まります。
もう1問考えてみましょう。

問題文を線分図に整理すると(図2)のようになります。

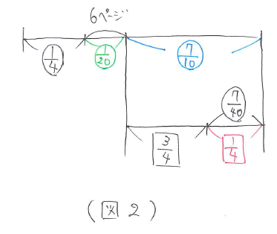
　前の問題と同じように考えて、マル7/40÷1/4＝マル7/10、マル1－(マル1/4＋マル7/10)＝マル1/20、
6÷1/20＝120(ページ)と求まります。
　難しく考えずに、最後に残った割合を普通の数字だと思って同じように計算します。

【第2位　平面図形：半径の値がわからなくても半径×半径の値で答えが出せます！】

　予習シリーズ5年上の第3回や第6回で学習した内容です。N角形に関する各公式や、円とおうぎ形に関する各公式などはしっかりと確認しておきましょう。

という問題を解いてみましょう。

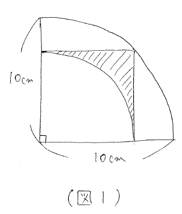
　円やおうぎ形の面積を求めるのに必要なのは、「半径」か「半径×半径」です。問題で「半径」がわからなければ、すぐに「半径×半径」を求められるように、頭を切り替えていきましょう。また、「半径×半径」は正方形や直角二等辺三角形の面積を利用することが多いです。　
小さい四分円の半径を□cmとすると、正方形の面積をひし形の公式を使って求めることで、□×□＝10×10÷2＝50　とわかります。したがって、斜線部分の面積は　50－50×3.14×1/4＝10.75(平方cm)と求まります。

【第1位　速さ：速さの和、差を使って解く方法を使いこなせていますか？】

　　予習シリーズ5年上の第16回、第18回、第19回で学習した内容です。速さの3公式はもちろん、旅人算の公式も使いこなせるようになるまで練習しておきましょう。特に旅人算では「速さの和」や「速さの差」に注目して考えられるようにしましょう。

という問題を考えてみます。
　3人の速さは全く分かりませんが、「速さの和」や「速さの差」に注目して考えていきます。AさんとCさんが10分ごとに出会いますから、AさんとCさんの速さの和は2400÷10＝240(m/分)となり、同じように考えてBさんとCさんの速さの和は2400÷15＝160(m/分)と分かります。A＋C＝240、B＋C＝160なので、AさんとBさんの速さの差は240－160＝80(m/分)になります。したがって、AさんがBさんを追い越すのは2400÷80＝30(分)ごとと求まります。
　速さの問題は公式を使えばすぐに解ける問題から、進行図をしっかりかかなければ解けないような問題まで幅広く出題されています。１つ１つ丁寧に解き直しをして、理解を深めながら学習していきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。