メールマガジン宝箱 Mail magazine

　5年生の皆さん、いよいよ後期最初のマンスリーを迎えます。クラスアップ実現のために、自分だけの復習ポイントを正確に見出しておきたいところです。
　そこで、対策ポイントを、プロ家庭教師の視点から第5位から第1位までのランキングのかたちにまとめました。ぜひ偏差値アップ、クラスアップを実現してください！応援しています！
　さらに、このランキングは明日公開の予想問題と連動していますので、予想問題も併せてご活用ください！
予想問題はこちらのページで1週間限定で無料公開します！

【第5位　売買損益：「全体の利益」の意味を正確に把握できていますか？】

　売買損益の問題では、価格の設定が何段階かに分かれるタイプの出題があります。その際に、「全体の利益」が示す金額を正確に算出できるかどうかが、得点のポイントになります。
　例えば次のような問題です。

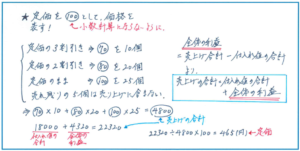
　このような価格が何種類も設定される場合には、それぞれの1個あたりの価格で考えてみましょう。
　定価をマル100とすると（マル1としてもよいですが、複雑な小数計算になるので、整数計算にできるように100と設定します）、10個はマル70、20個はマル80、25個はマル100のまま売ったことになります。
　ここでポイントになるのが、全体の利益です。全体の利益＝売上げ合計－仕入れ値の合計で求められますので、以下のような式が成り立ちます。
　売上げの合計＝仕入れ値の合計＋全体の利益
　この問題では、仕入れ値の合計が300×60＝18000（円）、全体の利益はその2割4分ですので、18000×0.24＝4320（円）となります。ここから、売上げの合計が、18000＋4320＝22320（円）と求められます（18000×1.24としても、もちろんOKです）。
　あとはマルで設定した価格を使って、
　マル70×10＋マル80×20＋マル100×25＝マル4800
　より、マル4800が22320円にあたることになります。ここに、売れ残った5個が売上げに含まれないことにも十分に注意してください。
　ここから定価のマル100が、22320÷4800×100＝465（円）となり、465÷300＝1.55から、定価は仕入れ値の55%であると求められます。
　この問題では価格が3段階でしたが、2段階に価格が設定され、その売上げ個数を求める際には、つるかめ算を使うことができます。

【第4位　正三角形の回転移動：直角の部分を曲がる際の角度を求められていますか？】

　正三角形の回転移動の問題の中でも、正三角形が直線上を回転する場合の点の動いたあとの線はスムーズにイメージをすることができますが、以下の図のような、折れ線の内部を回転移動するとなると、難度が上がってきます。

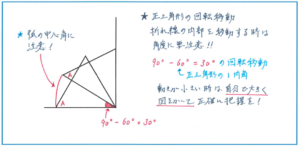
　実際に正三角形が回転する様子を自分で図にしてみると、頂点Ａが90－60＝30（度）回転していることがすぐにわかりますが、これを頭の中でイメージしてしまうと、正しく30度を思いつくまでに意外と時間がかかってしまいます。特にテストの際には、このような「小さな動き」は焦って値を取り違えてしまったり、動きを正確につかめなくなってしまうことが起こりえます。そうならないためにも、普段の演習の段階で、自分の手で大きく図をかいて回転移動を正確に把握しておくようにしましょう。

【第3位　円の移動：通らないカドの部分を正確に求められていますか？】

　同じく図形の移動の問題の中で、円が正多角形の内部を移動する時には、「通らない部分」を正確に把握することが求められます。
　円の移動でも、多角形の外部を円が転がる場合であれば解きやすいのですが、内部を転がる場合には、見落としがないように、より集中度を高めて臨む必要があります。　
　例えば次のような問題です。

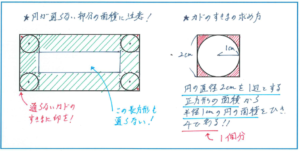
　まず解答の方針として、長方形全体の面積から、円が通らない部分の面積を引く、とすることに注意しましょう。円が内側を通過する図形が、正五角形などの、内側の通らない部分の面積が求められない場合は、円が通る部分の面積を求める解法になりますが、この問題のように内部の面積が求めやすい場合には、通らない部分を引く方が、計算が圧倒的に楽でミスを防ぎやすくなります。
　特にカドのすきまの部分の面積は、かたちが小さいことから見逃してしまいがちですので、上の図のように、通らない部分に点をつけるなどして、視覚的にも注意が払えるようにしておくとよいでしょう。
　問題の答えですが、通らない部分のうち、内側の長方形は、(6－2×2)×(12－2×2)＝16（平方cm）、すきま1つ分の面積が、（直径2cmを1辺とする正方形－円）÷4で、それが4つありますので、2×2－1×1×3.14＝0.86（平方cm）と求められます。よって、6×12－(16＋0.86)＝55.14（平方cm）となります。

【第2位　時計算：△回目に垂直になるパターンの解法をつかめていますか？】

　時計算は速さが角度で表されることもあり、苦手とされるお子様も多いかと思われます。特に次のようなタイプの問題はテストでも正答率がなかなか上がらない難敵です。

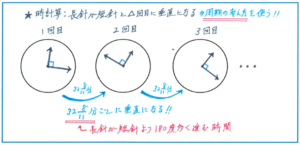
　問題を見て8回目という数字に難しさを感じてしまうかもしれませんが、実は周期の考え方を使えば、それが100回目でも計算で求めることができるのです。
　まずは初めて90度になるのが、長針が短針よりも90度多く進んだ時刻なので、
　90÷(6－0.5)＝180/11＝16・4/11（分）
　2回目に90度となる時点では、長針が短針よりも180度多く進んだことになりますので、1回目から、
　180÷(6－0.5)＝360/11＝32.8/11(分後)
となります。ここからは、32・8/11分ごとに90度になりますので、1回目から8回目までであれば、
　32・8/11×(8－1)＝2520/11＝229・1/11（分）
　よって、1回目までの時間を合わせて、16・4/11＋229・1/11＝245・5/11（分）より、6時間5・5/11分と求められます。
　長針が短針よりも多く進む角度を合計して、90＋180×(8－1)＝1350（度）としたうえで、
　1350÷(6－0.5)＝245・5/11
とすることもできます。
　周期で考える解法を身につけておきましょう。

【第1位　旅人算：2人と1人の出会い算はすべて線分図を使って解くと思っていませんか？】

　旅人算の問題では、状況を正確に把握するために線分図を使うケースがほとんどです。特に2人と1人が向かい合って進み、出会う時間に差が生じるタイプの問題では、線分図を使うことで式が断然立てやすくなります。
　ただ、次のような問題はどうでしょうか。

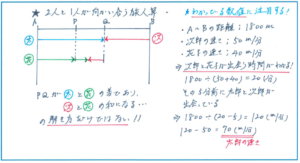
　2人と1人が向かい合って進むタイプの旅人算に慣れているお子様は、すぐに線分図をかいて解き進めようとされるでしょう。ただし、この問題では線分図に数値をかき入れようとしても、手が止まってしまうのです。というのも、線分図が抜群の効果を発揮するのは、3人の速さと、出会う時間の差が分かっていて、そこから全体の距離を求めるケースで、すべての場合に線分図が効果的に働くとは限らないのです。
　では、この問題はどう解けばよいのか。
　わかっている数値から内容を整理すると、次郎君と花子さんの速さから、この2人が出会うまでの時間が求められます。
1800÷(50＋40)＝20（分）
ここから「5分前」に太郎君と次郎君が出会っていますので（ここがポイントです！）、2人の速さの和が、
　1800÷(20－5)＝120（m/分）
となり、太郎君の速さを、
　120－50＝70（m/分）
と求めることができるのです。
　旅人算であればすべて線分図、と思い込まずに、問題文をよく読んで、わかっている数値をどう使うか考えることで、柔軟に問題に対応することができるようになります。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。