メールマガジン宝箱 Mail magazine

　5年生の皆さん、12月のマンスリーでは問題の内容に合わせて線分図・面積図を使い分けることが偏差値アップのポイントになります。相当算や和と差に関する問題では線分図を活用できるかどうかで、得点力に断然の差が生まれます。クラスアップ実現のためにも、図が的確に使えているかどうか、テスト前にしっかりチェックしておきたいところです。
　そこで、対策ポイントを、プロ家庭教師の視点から第5位から第1位までのランキングのかたちにまとめました。ぜひ偏差値アップ、クラスアップを実現してください！応援しています！
　さらに、このランキングは明日公開の予想問題と連動していますので、予想問題も併せてご活用ください！
予想問題はこちらのページで1週間限定で無料公開します！

【第5位　年令算：人数が複数になる場合は、マル1を使った式を活用しましょう！】

　年令算の問題で、例えば「現在、太郎君は7才、お母さんの年令は35才です。お母さんの年令が太郎君の年令の3倍になるのは何年後ですか。」といった基本パターンであれば、お母さんと太郎君の現在の年令を線分図で表し、その差（35－7＝28才）が変わらないことから、太郎君の年令を1、お母さんの年令を3とおいて、28才が3－1＝2にあたることから28÷2＝14から、太郎君が14才になる7年後、と答えに行き着くことができます。
　ところが問題に登場する人数が増えると、難度が一気に増してしまう印象が持たれがちです。確かに複雑にはなりますが、マル1を活用して、倍数算の考え方を使えば解法が見えてきます。
　次のような問題です。

　このタイプの問題では、迷わず求める年数をマル1としましょう。あとは式で内容を整理するだけです。

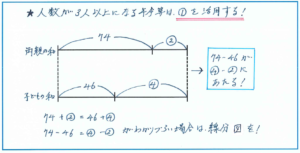
　マル1年後の両親の年令の和、2人の子どもの年令の和を式で表すと、次のようになります。
　　両親の年令の和…38＋36＋マル1×2＝74＋マル2
　2人の子どもの年令の和…13＋10＋マル1×2＝23＋マル2
　問題の、両親の年令の和が2人の子どもの年令の和の2倍ですので、
　　74＋マル2＝(23＋マル2)×2
　　　　　　　＝46＋マル4
　この式から、74－46＝28がマル4－マル2＝マル2にあたることから、マル1＝28÷2＝14より、14年後と答えを求めることができます。
　最後の式の処理を難しく感じる場合は、上のような線分図で整理してもよいでしょう。
　人数が増えても、このようにマル1を使った倍数算の考え方を使いこなせれば、難しさを感じることなく解き進めることができます。

【第4位　倍数算：和も差も一定でない問題を線分図で整理できていますか？】

　倍数算の中でも、2人の所持金が同じ金額増えたり減ったりするような差が一定の問題や、2人の間でやりとりをするような和が一定の問題は、線分図を使って解く基本的な問題となります。
それに対して、以下のような和も差も一定でない問題にはどのように対応すればよいでしょうか。

　このようなタイプの問題で、比例式を使って解くことができれば、問題を解くスピードは断然上がります。
　Ａ君とＢ君の初めの所持金を、マル7、マル5とすると、
　（マル7＋600）：（マル5－200）＝2：1
　ここで比例式の内項の積と外項の積が等しいことを利用します。
　（マル7＋500）×1＝（マル5－200）×2
　マル7＋500＝マル10－400
　ここから、マル10－マル7＝500＋400の式へのつながりがわかりづらい場合は、下のような線分図で整理しましょう。

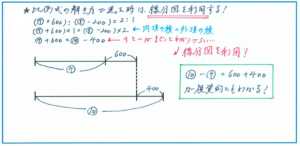
　マル3＝900より、マル1＝300となることから、初めのＡ君の所持金が300×7＝2100（円）と求めることができます。
　第5位の年令算の問題と同じく、式で解き進めるのが難しい場合は線分図を活用する解法をしっかり固めておきましょう。

【第3位　相当算：○ページ多く、△ページ少なくが混ざる時には線分図で整理を！】

　相当算の問題では線分図の活用は効果的ですが、特に次のようなタイプの問題では、線分図で数量の関係を整理しましょう。頭の中だけで解き進めようとすると、ミスを起こしてしまいます。

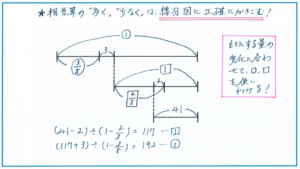
　問題に「残りの」とあるところで、もとにする量が変わることがわかるので、図のようにもとにする量をマルとシカクに使いわけることは相当算の基本になりますのでおさえておきましょう。
　ポイントは、2本目の線分図の上で2ページ少ない分をどのように表すか、という点です。ここで2ページ分を1本目と同じように割合の右側におかないように注意しましょう。あとは図から式を立てるだけですが、無理にひとつの式にまとめようとせず、式をわけて確実に値を求めていく方がミスを防げます。
　(41-2)÷(1-23 )＝39÷13 ＝117
　(117＋3)÷(1－38 )＝192
　よって本は全部で192ページと求められます。
　細かな点ですが、数の増減を間違えてしまうだけでミスにつながりますので、ひとつひとつ確実に式を立てていきましょう。

【第2位　和と差に関する問題：個数とり違えの問題では面積図が効果的です！】

　和と差に関する問題の中で、個数をとり違えてしまうタイプの問題では、2つの量の大小関係がわかりづらくなってしまうことがあります。そこで面積図を使ってみると、個数の大小に関わらず式を立てることができます。
　例えば次のような問題にはどのように対応すればよいでしょうか。

　予定と逆に買ってしまったために金額が不足したので、予定では150円のノートの方が多かった、ということがすぐにわかれば、60÷(180－150)＝2より、12冊のうち150円のノートが180円のノートよりも2冊多く買うということから和差算の考え方で(12－2)÷2＝5（冊）と答えに行き着くことができます。

　最後の和差算の考え方を使うことまではわかっても、2つのノートの数量の大小関係がわからなければ、式が立てられなくなってしまいます。そこで、上のように、面積図を上下逆さまして、くっつけたかたちで考えてみましょう。
　下の大きな長方形の面積は、12×(180＋150)＝3960と求められます。
　予定ととり違えて60円不足したので、上のくる図形が下の図形よりも60多くなります。そこで面積の和差算の考え方で、(3960－60)÷2＝1950が下の図形の面積（予定の金額）です。あとは、つるかめ算の考え方で、(1950－150×12)÷(180－150)＝150÷30＝5より、予定していた180円のノートの冊数が5冊と求められます。
　この解法であれば、予定ではどちらを多く買うのか、よいった点で迷わなくて済むメリットがあります。ぜひ試してみてください。

【第1位　和と算に関する問題：じゃんけんの問題で合計点に注目できていますか？】

　和と差に関する問題の中で、じゃんけんの問題、特に「あいこ」が含まれる問題では、合計点に注目すると、正解までの道筋がハッキリと見えてきます。
　次のような問題を例にして解法を考えてみましょう。

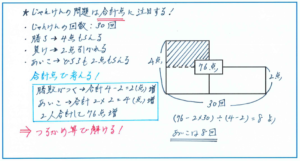
　ここで「あいこ」をどう扱うかが悩ましいところですが、Ａ君、Ｂ君のどちらが勝ったか、あいこになったかといった結果に注目してしまうと、なかなか解法が浮かんできません。
　そこで、点数の合計に注目してみましょう。どちらが勝ったとしても勝敗が決まれば、2人の合計点は1回につき、4－2＝2（点）増えます。一方、あいこになった場合は、2人に2点ずつ与えられるので、合計にして2＋2＝4（点）が増えます。
　次に2人の持ち点に注目します。2人の合計点は144＋132＝276（点）、はじめの持ち点の合計は100×2＝200点ですので、2人合わせて276－200＝76（点）が増加したことになります。
　30回のじゃんけんで、勝ち負けが決まった場合は2点増加、あいこの場合は4点増加、合計で76点増加、となれば、つるかめ算が使えます。
　(76－2×30)÷(4－2)＝16÷2＝8より、あいこが8回と求められます。
　このようなゲームでの点数を題材とした問題では、どちらが勝ったか、よりも合計点がどれだけ増えたか、に注目すれば、一気に正解に近づくことができます。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。