メールマガジン宝箱 Mail magazine

　4年生の皆さん、12月マンスリーでは問題を速く正確に解く工夫が偏差値を押し上げ、クラスアップを実現します。3.14計算の工夫や式の書き出し方といった基本的なことから、深さの変化での断面図の書き方など、ひと工夫するだけで絶大な効果を生み出すのです。そこで対策ポイントを第5位から第1位までランキングにしました。ぜひ偏差値アップ、クラスアップお役立てください！応援しています！
　さらに、このランキングを実践的に身につけられるように予想問題を作っていますので、予想問題も併せてご活用ください！予想問題のショートバージョンは、こちらから無料でダウンロード頂けますので、ぜひご活用ください！
　さらに、クラスアップ答練会では、フルバージョンの予想問題と解説動画もご覧いただけます！

【第5位　円とおうぎ形：1ケタ×3.14の計算結果を覚えられていますか？】

　円とおうぎ形の問題では、長さ、面積どちらを求める際にも3.14の計算を早く正確に行う必要があります。せっかく式を正しく立てられても3.14計算で間違えてしまっては、得点のチャンスを逃してしまいます。
そこで、3.14計算を正確に行うための3つのポイントを挙げてみましょう。
(1) 3.14計算はまとめて最後にする。
(2) 1ケタ×3.14の計算結果は覚えておく。
(3) 筆算では3.14を上に置く。

　まず(1)の3.14計算をまとめて最後にするという点は、塾でもくりかえし注意するように言われているでしょう。3.14に限らず、そもそも小数第2位の数を計算するとなると、どうしても計算ミスを起こしやすくなってしまいます。計算ミスを防ぐためには計算の回数を少しでも減らすことがポイントになります。3.14計算は最後にまとめてするようにしましょう。
　計算する回数を減らしても、やはり3.14計算は面倒なものです。そこで、少しでも負担を軽くするためにも、以下の1ケタ×3.14の計算結果は覚えてしまいましょう。

1×3.14＝3.14
2×3.14＝6.28
3×3.14＝9.42
4×3.14＝12.56
5×3.14＝15.7
6×3.14＝18.84
7×3.14＝21.98
8×3.14＝25.12
9×3.14＝28.26

　ひたすら書いて覚えるのでも、口でくりかえし唱えて覚えるのでも構いません。暗記に少し時間がかかるかもしれませんが、覚えることの効果は絶大ですので、頑張って覚えてください。
　(3)の筆算の書き方は、ほんの些細なことに見えて、大きな違いを産むものです。特に1ケタ×3.14の計算結果を覚えておくと、かけ算は不要になり、たし算をするだけで正解に行き着くことができるようになります。筆算の段階ですぐに3.14を上に置けるように、頭の中に刷り込んでおきましょう。

【第4位　平均算（復習）：平均から求めた和の書き出し方が正解のポイントです！】

　11月マンスリーの範囲でもあった平均算ですが、与えられた平均と個数から全体の和を求める際には、和を表す式の書き出し方の違いで、速く正確に問題を解けるかどうかの大きな差を生み出します。
　例えば、太郎君、次郎君、三郎君の3人が10点満点のテストを受けて、その点数の平均を以下のようにまとめたとします。
・3人全員の平均は、7点
・太郎君と次郎君の平均は、8点
・太郎君と三郎君の平均は、6点
　ここで太郎君の点数を求めるとした際、まず平均から合計点を出す、という流れまではすぐに思いつくでしょう。ポイントはその合計点を表す式の書き出し方です。

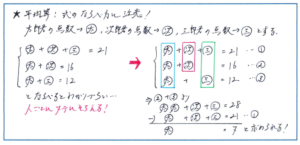
　左の図のように、ただ左をそろえて並べるよりも、右の図のように、人ごとに縦をそろえたかたちの方が、点数の関係がつかみやすく、また解き方にも幅ができます。もちろん「①の式から②の式を引いて、まず三郎君の点数を求めて、①の結果から三郎君の点数を引く」というかたちでもよいですが、式の並びを見て、②の式と③の式を足した結果、太郎君だけが2つ分になることから、「②の式と③の式の和から①の式を引く」という解き方に気づくと、計算は楽になります。
　細かな違いのようですが、この例では3つの要素なのが、その数が増えた場合、後に挙げた方法を身につけておくと、スムーズに計算を進めることができるようになりますので、式のならべ方には十分注意してください。
　制限時間のあるテストでは、このような式の書き方ひとつでより時間を短縮できる効果が望めます。

【第3位　円とおうぎ形：おうぎ形と三角形の面積の関係を正確に見つけ出しましょう！】

　マンスリーテストでは、円やおうぎ形そのものの面積を求める問題だけではなく、円やおうぎ形の中に三角形が含まれるなどの複合的な問題も出されます。そうした問題に対応するためには、円やおうぎ形以外の図形の面積を正確に求める力が必要になります。
　例えば下の図の斜線部分の面積を求めるといった場合、おうぎ形の面積から直角二等辺三角形の面積を引くという解き方はすぐに浮かぶでしょう。そこで三角形の面積を早く正確に求めなくてはなりません。底辺と高さがわかっていなくても、図のように直角二等辺三角形を2つ重ねて面積が求められるような工夫ができるように、直角二等辺三角形の性質そのものをしっかりつかんでおくようにしましょう。

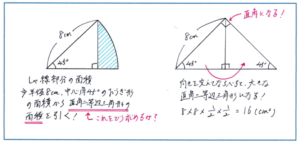
　これから5年、6年と学年が上がることで、おうぎ形の中心角が図のような45度ではなく、30度や60度となるなど、図形の複雑さが急激に増してきます。そうした問題に対応できるようになるためにも、まずはデイリーサピックスに出てくるような中心角が90度のおうぎ形、今回取り上げたような45度の基本的なパターンで正解できるように、図形の見方を鍛えましょう。

【第2位　グラフの読み取り方：量の変化をつかむためにグラフの傾きに注目しましょう！】

　グラフの傾きを見る際に、例えば傾きが水平になるのが、量が増えずに時間が経過するということはわかりやすいのですが、傾きが急になったり緩やかになったりする変化がなぜ起こるのか、について確実に答えられるようにしておきましょう。グラフ問題では、問題の内容がどのようにグラフに反映されているのかを、どれだけ速くつかめるかが得点アップのポイントになります。まずはグラフの基本的な成り立ちを確実におさえておきましょう。

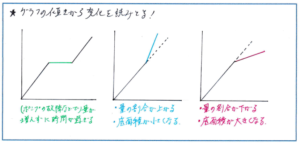
　図にあるように、傾きが急になるのは「量の割合が上がる時（水を入れる問題では時間あたりに入れる水の量が増える時）」または「容器の底面積が小さくなる時」、傾きがゆるやかになるのは「量の割合が下がる時」または「容器の底面積が大きくなる時」となります。特に底面積との関係をしっかりつかんでおくと、複雑な形をした容器が問題になった際に解き方が定めやすくなります。

【第1位　深さの変化：水が入った容器におもりを入れるパターンで確実に得点を！】

　深さの変化の問題は、「水の中に入ったおもりの体積＝見かけ上増えた水の体積」の考え方で解き進めます。おもりが完全に水の中に沈むタイプの問題は、水の体積が見かけ上増えることのイメージが比較的持ちやすいのですが、図のような高さのあるおもりを沈めるパターンになると、見かけ上増えた水の体積がどれだけになるのかが、わかりづらくなります。
　対策としてはおもりを沈めたかたちを右のような断面図にして、視覚的に体積を把握することが重要です。図のアの部分とイの部分の体積が等しくなることだけでなく、ア＋ウ＝イ＋ウの関係をつかんでおくと、特に「容器（水そう）の底面積を求めなさい」といった出題に対応することができます。

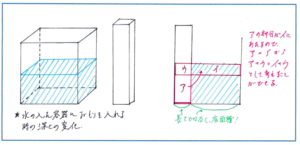
　断面図では、横の長さが底面積を表すことをしっかりつかむようにしてください。これは面積を便宜的に長さに置き換えているのですが、この「便宜的」という考え方が4年生の段階ではまだ難しく感じられてしまいます。体積を平面で表すために、面積が長さになる、といった流れで考えるとよいでしょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。