メールマガジン宝箱 Mail magazine

　12月度マンスリーでは割合と比をフル活用して解く問題が多く出されます。線分図などで内容を整理することはもちろんですが、割合と比をどのように記号にするか、どのような数値をおくと解きやすくなるのかを身につけることで得点アップ、偏差値アップ、クラスアップを実現できます。そこで対策ポイントを第5位から第1位までランキングにしましたのでお役立てください！
　さらに、このランキングを実践的に身につけられるように予想問題を作っていますので、予想問題も併せてご活用ください！ショートバージョンは、こちらから無料でダウンロード頂けます！

【第5位　比と図形：相似な図形の対応する辺を正確にとらえられていますか？】

　11月マンスリーの範囲でもありました「比と図形」ですが、相似の関係を利用する際に、対応する辺を間違いなくとらえられていますでしょうか。対応する辺さえ把握できれば、そこからの比の計算は正確に進められます。5年生のこの時期のマンスリーや組分けともなれば、一見して相似の関係が理解できるような単純な図形ではなく、例えば下の左の図のような向きが左右で異なる図形を重ねたものや、図形を折り返すことによって生まれる相似の関係を見つけさせる問題が多く出されるようになります。

　正確に対応する辺を見つけるためには、まず対応する角度を○や●といった同じ記号で表し、さらにその記号の並び方をもとに対応する辺を見極めてゆけば、間違いを防ぐことができます。Ａ→Ｂ→Ｃと、辺をペンでなぞって対応する辺を見つける方法も時間を短縮するうえではよいのですが、少しでも間違う可能性を低くするためには、簡単な表で整理することが有効です。テストの際に表の作成を短い時間で済ませられるように、ぜひ練習をしてみてください。

【第4位　倍数算：和も差も一定でない問題の「比例式」で計算間違いしていませんか？】

　倍数算の中でも、2人の所持金が同じく増えたり減ったりするような差が一定の問題（兄と弟がそれぞれ同じ金額を使った場合の比の変化など）や、2人の間でやりとりをするような和が一定の問題（兄が弟に200円渡した場合の比の変化など）といった基本的な問題であれば、線分図がかいてすぐに式が立てられるでしょう。
　それに対して、例えば「Ａ君とＢ君の所持金の比は7：5でしたが、Ａ君は500円もらい、Ｂ君は200円使ったので、2人の所持金の比は2：1になりました。」といったタイプの問題では線分図で内容を整理しようとしても、図が大きくなりすぎるなど、対応しづらくなってしまいます。そこで比例式を使って解くことが正解に至るポイントになるのですが、この比例式を解く際に、特にプラスとマイナスでの間違いが起きやすくなります。
　そこでそうした間違いを防ぐ2つの方法をお伝えします。

　まずは式の処理の仕方です。数学を学習していれば、「移項」の考え方は方程式の最初に習いますが、マイナスの概念を学んでいない小学生のお子様方にとって、この移項の考え方は親御様が思う以上に難しいものです。そこで、「両辺に同じ作用をしても等号（＝・イコール）の関係は変わらない」という式の基本に立ち返って、段階的に式を処理して行きましょう。「邪魔なものを消す」という基本方針を念頭に置いて、まずはマル数字の小さい方に着目して、両辺からマル7を引きます。続いて両辺に400を足すことで、右辺にある400が消えます。これでマル3が500＋400＝900（円）となることから、マル1が300円と求められます。
　結局は移項をしたことと同じなのですが、いきなり「＝をまたぐとプラス、マイナスが入れ替わる」と機械的に覚えるよりも深く理解を固めることができ、ミスを減らすことができます。
　また、この式の処理を線分図で進めれば、視覚的に理解を進められます。上の図のように、比例式を解き進めて、マル7＋500＝マル10－400の式になった段階で、Ａ君とＢ君の所持金を線分図にすると、2つの量の関係が一目のうちに把握でき、マル3＝500＋400となることが、瞬時に理解できます。
　慣れてしまえば、式を段階的に処理したり線分図をかかなくても、すぐに式を解き進められるようになりますが、計算ミスが目立つようでしたら、一度そうした解法に立ち返ってみてください。時間がかかるようですが、計算ミスをなくす近道になります。

【第3位　流水算・通貨算：割合と比を使う問題で式を正しく立てられていますか？】

　11月マンスリーの範囲でもあった流水算・通貨算の問題の中で、割合と比の考え方を使って解く問題では、問題内容を図などで整理する際に、割合や比をどのように式に反映させるかが正解に至るポイントになります。
　流水算で言えば川の流れの速さや船の静水時の速さが変化するタイプの問題で、割合と比を使うことが求められます。例えば「下りの速さが時速12㎞の船が、上りの際に静水時の速さを1.2倍したら時速10㎞になりました。川の流れの速さは時速何㎞ですか。」といった問題。線分図をかいて内容を整理してもよいのですが、下りの静水時を速さマル5、上りの静水時をマル6、川の流れの速さを□とすることで、下の（図1）のように、消去算に持ち込むことができるのです。
　また通過算であれば、例えば長さ200mで速さ時速80㎞の列車Ａが鉄橋を通過する時間と、長さ300mで速さ時速90㎞の列車Ｂが鉄橋を通過する時間が同じだった場合、鉄橋の長さは何mですか。」といった問題では、まず速さと比の基本である、同じ時間であれば、速さの比＝道のりの比となることを踏まえて、列車Ａが進んだ道のりをマル8とすると列車Ｂが進んだ道のりがマル9と表されるところまでは、スムーズに仕上げておきたいところです。
　ここからは下の（図2）のような図を使うなどして、道のりの差であるマル9－マル8＝マル1が列車の長さ300－200＝100（m）にあたることから、鉄橋の長さを、マル8－200＝800－200＝600（m）と求めることができます。

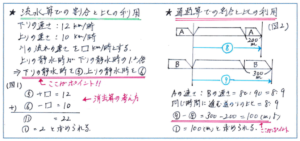
　先月のマンスリーの復習を通して、流水算であれば、上りの速さ・下りの速さの関係、通過算であれば列車の長さの式への取り込み方といった基本をまずはしっかり確認したうえで、ご紹介したような割合と比をからめた解法までしっかり理解しておくようにすれば、得点力が大幅にアップします。

【第2位　相当算：割合の計算をしやすくするために、問題の「同じ部分」に注目しましょう！】

　相当算の問題では、線分図に問題で与えられた割合を書き込んで、割合と実際の数量の関係（2/5が40ページにあたる、など）がつかめれば、一気に正解まで突き進むことができます。
　ポイントは割合の表し方です。次のようなタイプの問題で、線分図に書き込む割合の数値の置き方にひと工夫をすると、断然解き進めやすくなります。
　「ある本を1日目に全体の2/9よりも22ページ多く読み、2日目に残りの2/5を読んだので、残りは全体の3/8が残りました。この本は全部で何ページありますか。」といった問題ですが、線分図を下のようにかくのに大きな苦労はないでしょう。

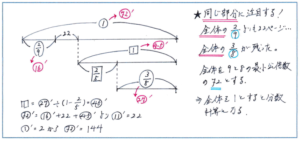
　問題は割合の書き込み方ですが、もちろん全体を「1」としても解き進めることはできますが、分数計算が必要となるため、分数計算が苦手なお子様ではなくても、ミスが多く起きてしまいがちです。
　そこで全体を1以外の数と置いて、整数計算で進められるようになれば、と考えてみます。1日目と2日目では割合のもとにする量が変わってしまいますが、1日目と3日目で使われる割合のもとにする量はどちらも「本全体のページ数」で共通しています。そこで1日目と3日目の割合の分母の9と8の最小公倍数である72を全体とします。
　大事なのは、ここで線分図に示した割合を別の記号（マルダッシュなど）を使って書きかえる（上書きする）ことです。全体をマル1からマルダッシュ72に変えて、それに合わせて記号をマルダッシュに統一します。これでマルダッシュ72＝マルダッシュ16＋22＋マルダッシュ45となることから、マルダッシュ11＝22より、マルダッシュ1＝2となり、本は全部で2×72＝144（ページ）と求められます。
　今回ご紹介した数のそろえ方は一例ですが、全体の数を1以外にすることは計算を楽に、結果として正答率を上げるために大事な考え方となります。そこで全体の数をどのような値にするか、そのために問題をよく読んで「同じ量」に注目するようにしましょう。

【第1位　和と差に関する問題：過不足算の長いす型の問題は図で内容を整理しましょう！】

　過不足算の中でも長いす型の問題は、言葉の意味の取り方を間違えてしまうなどの理由で、失点しやすくなってしまいます。通常の過不足算であれば簡単に式を立てられるのが、長いす型になると式をどう立ててよいのか迷ってしまう。その要因のひとつは、長いすが余る、不足する状況と、そこに座る人が余ったり不足したりする関係が、言葉からではなかなかわかりづらいところにあります。
　このタイプの問題では、あくまで「人」に着目して図をかくことで、内容がグッとわかりやすくなります。長いすの数ではなく、人の数で見比べることに注意して、図をかいてみましょう。

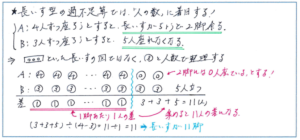
　ここで気をつけるのは、「長いすが○脚余る。」「□人が座れなくなった。」といった状態のうち、特に前者の長いすが余るパターンです。あくまで人の数に注目をして、「あるべき長いすに座る人数が0人であった」と視点を切り替る必要があります。
　上の例で言えば、4人ずつ座ろうとすると長いすがちょうど2脚余る、ということは、「2脚には0人が座っている」、と考えます。ここで4×2＝8人を考えないように注意してください。そこで比較の対象である3人ずつ座ろうとすると5人座れなくなる、という状態とを比べると、3×2＋5＝11人が2つの状態での人数の差となりますので、これを1脚ずつの人数の差、4－3＝1で割ることで、「座っている」長いすの数が11脚（これを長いすの総数としないこと！）、人数が4×11＝44（人）と求められます（3×(11＋2)×5＝44（脚）としても求めることができます）。
　これを踏まえて、特に注意して頂きたいのが「最後の1脚だけ△人は座りませんでした」といった場合です。上記の例と同じように図にまとめるまでの流れは同じですが、最後の1脚の部分については、「△未満の数で場合分け」をすることになります。△人が4人であれば、1人、2人、3人と場合分けして、それぞれに関して長いすの数を求める計算をすることになります。
　この長いす型の過不足算は、最後の計算に至るまで、図なしで頭の中だけで解こうとすると、計算でミスをしてしまうことが、とにかく多くなってしまいます。今回ご紹介した図以外にも面積図で解く方法もあります。テストの時に使いやすい方で構いませんので、図のかき方を徹底的に練習しておきましょう。
　
　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。