メールマガジン宝箱 Mail magazine

　新6年生になって最初のマンスリーテストです！今回のマンスリーでは、速さと比の問題やニュートン算での線分図、食塩水の濃度での面積図やビーカー図など、問題内容を正確に図でまとめることが求められます。その他にもN進法や場合の数も含まれ、幅広い範囲からの出題となるテストになります。そこで2月度マンスリーテストの対策ポイントを第5位から第1位までランキングにしましたので、ぜひマスターしてテストに臨んでださい！応援しています！
　さらに、このランキングを実践的に身につけられるように予想問題を作っていますので、予想問題も併せてご活用ください！ショートバージョンは、こちらから無料でダウンロード頂けます！

【第5位　Ｎ進法：予想を立てる→確かめる、の流れを身につけられていますか？】

　Ｎ進法の問題は、問題を解く流れを理解して解き方をしっかり覚えられていれば難しくないのですが、解き方を覚えていない、あるいは曖昧な理解にとどまってしまっていると、手も足も出なくなってしまいます。問題によっては、問題文を読んですぐにＮ進法を使って解けるとは気づかないようなタイプのものもあります。
　特に図形や記号を使った問題では、Ｎ進法の解き方を使うかどうかの判断が難しくなります。数の変化を注意深く見て、的確に予測を立てたうえで、それを検証するという流れをできるだけ早く身につけておきましょう。
　例えば下の図のような問題では、2を表す図と3を表す図の違い、5を表す図と6を表す図の違いから、マスが3になるとひとつ左のマスに移る、という変化が見られることから、この数の表し方が「3進法」ではないか、との予想が立てられます。それを他の7や8、9といった数で確かめることで、図が「3進法」を表しているとの結論に至ることができるのです。
　そのうえで、例えば「21」を図にする場合であれば、21÷9＝2あまり3となることから、右から3つ目のマス2つともに○を入れて、2つ目のマス1つに○を入れればよいことになります。

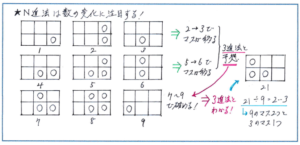
　Ｎ進法の問題では、問題の中で数の例が出されますので、その例から数の変化の規則を見つけ出し、「□進法である」との予想を立てて、他の例でその検証をする、といった流れを時間をかけずにできるように練習を重ねておきましょう。

【第4位　場合の数：「より少ない方を使う解法」は使いこなせていますか？】

　場合の数の問題では、問題をよく読んで解き方をほんの少し工夫すれば、解くスピードと正確さに大きな差が生まれることがあります。問題文に書かれた条件から、どのように解き進めれば計算が楽になるかを考える意識を持って問題に臨むようにしましょう。
　例えば、「形も大きさも同じ赤いボール4個、青いボールが2個、全部で6個あります。この6個のボールを1列に並べるとき、並べ方は何通りありますか。」といった問題を例にしましょう。
　まずポイントになるのが、「形も大きさも同じ」ボールであること。同じ6個のボールでも、番号が入っているなど、ひとつひとつのボールを区別できる場合と、この問題のように区別ができない場合で解き方が異なることは、すぐに判断できるようにしておきたいところです。ボールを区別できないパターンでは、ボールの並べ方を求めたうえで、重複する並べ方の場合の数でそれを割ることを忘れないようにしましょう。ここまでは基本的な解法ですので、この点での理解が曖昧な場合は、テストまでに重点的に復習をしておくようにしてください。
　そのうえで問題を解く最初の段階である「ボールの並べ方」について、工夫ができないか考えてみましょう。6個のうち赤いボール4個を並べる場所が決まれば、残り2つの枠は自動的に青いボールの場所になります。ということは、逆に青いボール2個を並べる場所を決めてしまえば、残り4つの枠が自動的に赤いボールの場所になるとも言えます。そこで数が小さい「2個」の方を選んで計算を進めれば、速く正確に計算を進めることができるのです。

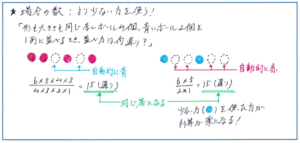
　場合の数では、このような「残り」や「あてはまらない方」に着目した方が断然解きやすくなるパターンが数多くあります。例えば「3、2、1、0の4枚のカードを並べて3ケタの整数をつくるとき、300より小さい数は全部で何個ありますか。」といった問題でも、あてはまる整数である、百の位が2か1となる整数の個数をそのまま求めるよりも、つくり得る全ての3ケタの整数の個数から、300以上の整数の個数を引いた方が、あてはまる場合が少ないことで計算が楽になり、ミスも防ぐことができます。
　限られた制限時間の中で少しでも多く得点を重ねるためにも、計算が楽にできるような工夫がないか、意識するようにしましょう。

【第3位　ニュートン算：線分図をかいて問題内容を整理する流れを確認しておきましょう！】

　ニュートン算は、線分図を使っていかに問題内容を正確に把握するかが、得点力アップのポイントになります。ニュートン算は出題のされ方がパターン化されていますので、問題を見てニュートン算の考え方を使えばよいと判断できることが他の単元よりも多いと言えます。まずはニュートン算の出題パターンを頭の中にしっかり植え付けておきましょう。
　あとは正確な線分図がかけるかどうかのチェックを欠かさないようにしてください。例えば、「毎日一定の割合で草が伸びる放牧場があります。この放牧場で、牛9頭を放し飼いにすると35日で生えている草がなくなります。また、牛15頭を放し飼いにすると14日で生えている草がなくなります。この放牧場で、牛25頭を放し飼いにすると、何日で生えている草がなくなりますか。」という問題では、どのように線分図をかけばよいでしょう。

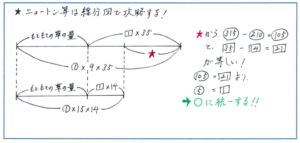
　線分図をかく流れについて念のため確認しておきましょう。
　まず、上のように2本の線分図をかき、左端にもともとあった量（この問題では、もともと放牧場に生えていた草の量）を置きます。次に単位量あたりに減る量をマル1、増える量をシカク1とします。
　ここで、「線分図の差からマル1とシカク1の関係を式にして、どちらかの記号に統一する」ことが解法のポイントになります。
　この流れで進めると、まず牛9頭を放し飼いにした場合は、35日で牛が食べる草の量がマル315、牛15頭を放し飼いにした場合は、14日で牛が食べる草の量がマル210となります。
　線分図の長さの差を、マルとシカクで表すことで、マル315－マル210＝シカク35－シカク14より、マル105＝シカク21からマル5＝シカク1となります。
　そこで記号をマルで統一すると、もともと放牧場に生えていた草の量がマル315－マル5×35＝マル140と表せることになります。
　最後に、牛25頭が1日に食べる草の量がマル25、1日に生える草の量がマル5となることから、140÷(25－5)＝7より7日と答えが求められます。
　ニュートン算では線分図をかくことが正確に問題を解き進めるうえで重要にはなりますが、いつでも線分図が必要、ということではありません。もともとあった量（上の問題であれば、もともと放牧場に生えていた草の量）がわかっているタイプの問題であれば、図をかかなくとも式で正解まで行き着くことができるケースがあります。問題内容によって、より短い時間で、かつ正確に解ける方法を身につけておきましょう。

【第2位　食塩水の濃度：「濃さが等しくなる」場合の解き方を覚えていますか？】

　食塩水の濃度の問題では、特に異なる濃度の食塩水を混ぜ合わせるタイプの問題に注意が必要です。いくつかの種類の食塩水について、「容器Ａから容器Ｂに何グラムか移し、その後、容器Ｂから容器Ａと容器Ｃに同じ量の食塩水を移す…」といった、やりとりの問題はテスト終盤の応用問題として出題されることが多く、得点できるとテスト全体の偏差値アップの実現につながります。そうした問題では、ビーカー図を使って混ぜ合わせのやりとりを正しく把握することが大事ですので、時間をかけずにビーカー図をかくことをポイントに、復習をしておきましょう。
　やりとりと合わせて気をつけて頂きたいのが、「混ぜ合わせた結果、食塩水の濃さが等しくなる」というパターンの問題です。
　例えば、「容器Ａには15%の食塩水が200グラム、容器Ｂには3%の食塩水が400グラム入っています。Ａ、Ｂからそれぞれ等しい量の食塩水をくみ出し、Ａからくみ出した分はＢに、Ｂからくみ出した分はＡに入れてよくかきまぜると、ＡとＢの食塩水の濃さは等しくなりました。くみ出した食塩水の量は何グラムですか。」といった問題。

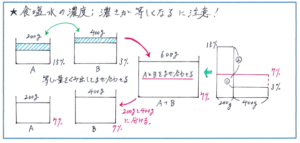
　面積図や天びん図を使って解くことにはなりますが、くみ出した食塩水の量がわからないので、すぐには図をかき始められません。ポイントは、「等しい量の食塩水」をやりとりした点です。この問題では、食塩も水も新たに加えることなく、Ａの容器の食塩水は200グラム、Ｂの容器の食塩水は400グラムのままで変わっていません。その状態で混ぜ合わせた後の2つの容器の濃さが等しくなりますので、上の図のような、大きなビーカーにＡ、Ｂそれぞれの食塩水を入れてよくかきまぜて、それをＡに200グラム、Ｂに400グラム戻した、と考えることができるのです。
　大きなビーカーにある600グラムの食塩水の濃さは7%になりますので、ここからは容器Ａのみに注目すると、「15%の濃さの食塩水と3%の濃さの食塩水を混ぜ合わせると、7%の食塩水200グラムになりました。」と考えられます。
　あとは面積図・天びん図を使えば、200×2/3＝400/3より、移した食塩水の量を400/3グラムと求めることができます。
　食塩水の濃度の問題では、面積図・天びん図、あるいはビーカー図など、様々な図を用いて問題内容を整理することになりますが、今回ご紹介したような、図をかく以前に気づくべきポイントを逃さないように問題文の読み取りに十分に注意しましょう。

【第1位　速さの問題：問題を解きやすくなる線分図がかけていますか？】

　速さの問題を解く際に線分図が有効な武器となることは言うまでもありませんが、問題を解くために必要なポイントを的確に図に盛り込ませることができれば、解答にかける時間を大きく縮められ、不用意なミスを減らすことができます。
　特に速さの問題では時間の経過を正確に読みとる必要があり、そのためにも時間が経過する様子も線分図に含められるようにしておきたいところです。そこで、「同じ時刻に印をつける」という作業を取り入れてみましょう。例えば「弟は8時に家を出て毎分60mの速さで学校に向かいます。兄は8時10分に家を出て毎分80mの速さで学校に向かいます。兄が学校に着いた時刻に弟は学校の200m手前のところにいました。家から学校までは何mですか。」と言った問題では、どのように線分図をかけばよいでしょうか。

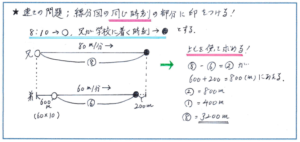
　この問題のように時間のずれがある問題は、それだけで問題の難度が上がってしまいます。また、始業時刻がわかっていないことで、さらに解き方が難しくなります。こうした問題で正解できれば確実に得点差を生み出すことができるのですが、そのためにも時間のずれを図で的確に表す必要があります。上の図のように同じ時刻を○や●といった記号で表すことができれば、「同じ時間」の部分を一目で把握できます。この「一目で」がテストの際には時間短縮のポイントになるのです。
　同じ時間に着目ができれば、あとは比の出番です。6年生になると比を使う問題が出されるケースがとても多くなります。もちろん速さの問題も比をからめた出題になるケースが多く、その際に「同じ時間であれば、速さの比＝距離の比」「同じ距離であれば、速さの比と時間の比は逆比の関係」の関係は確実に使いこなせるようにしておきましょう。この問題では、○→●が同じ時間ですので、この部分の線分の長さの比が2人の速さの比である、80：60＝4：3となり、差の1が60×10＋200＝800（m）となるので、家から学校までの距離が800÷(4－3)×4＝3200mと正解に行き着くことができます。
　入試頻出の速さと比の問題は、これからもサピックスのテストで多く出題され、難度も大きく上がってきます。難問に対しても線分図で内容を整理する習慣が身についていれば、得点のチャンスも大きく広がりますので、今のうちから線分図の活用方法に慣れておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。