メールマガジン宝箱 Mail magazine

　5年生として最後の組分けテストです！新6年生を今よりも上位のクラスで迎え、よりよいかたちで受験最終学年のスタート切るための大事なテストとなります。理解があいまいな部分は少しでもなくしておきたいところです。そこで第9回組分けテストの対策ポイントを第5位から第1位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！
　さらに、このランキングを実践的に身につけられるように予想問題を作っていますので、予想問題も併せてご活用ください！ショートバージョンは、こちらから無料でダウンロード頂けます！

【第5位　第11回から第14回の復習：時計算の応用パターンに対応できていますか？】

　テスト全体の点数にして約3割を占めます。前回のテストでもう一歩で得点できなかった単元を中心に基本事項を確認しておきましょう。特にニュートン算は基本的な解き方が固まっていれば得点のチャンスは大きく広がりますので、線分図のかき方などを見直しておくとよいでしょう。
　速さの問題のうち時計算では、「7時と8時の間で時計の短針と長針が重なる時刻」などの基本的な問題だけでなく、応用パターンにも対応できるようにしておく必要があります。
　例えば、「7時24分48秒のときに、長針と秒針の作る角度で、小さい方の角度は何度ですか。」といった問題では、秒針の進む速さまで考えなくてはなりません。

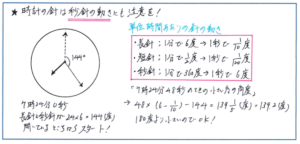
　長針と短針が重なる問題で、「角度の差を5.5で割る」といった計算をただ覚えて解くなど、暗記に頼ってしまっているばかりでは、出題のかたちが少し変わっただけで対応ができなくなってしまいます。長針は1分間に6度、短針は1分間に0.5度進むので、2つの針の差は1分間に6－0.5＝5.5（度）縮まることから「5.5で割る」となる流れをしっかり把握しておくなど、解法の内容をしっかり理解しておけば、長針と秒針の関係でも、1秒間に長針が6÷60＝1/10（度）、秒針が1秒間に360÷60＝6（度）進むので、1秒間に長針と秒針の角度の差が(6－1/10)度縮まると考えられるのです。
　時計算で見られる応用問題は、数値を暗記するのではなく、なぜその数値になるのかを理解していなければ問題の出され方が変わった際の対応力が求められる端的な例のひとつと言えます。暗記にとどまらない解法を少しでも多く身につけておきましょう。

【第4位　年れい算：線分図のかき方の工夫はできていますか？】

　年れい算の問題では、線分図を活用して年れいの差を的確に把握することがポイントになります。年れい算では、「○年後に父親の年れいがＡ君の年れいの□倍になる」といった、時間の経過が含まれる点が問題の難度を上げる要素となります。その時間の経過を線分図に反映させるには、線分図のかき方に工夫が必要です。
　「現在、父親は43才、Ａ君は11才です。父親の年れいがＡ君の年れいの5倍だったのは、今から何年前でしたか。」といった問題で、現在の父親、Ａ君の年れいを表す線分図をかく際に、□年前の部分をどのように図にするかが重要になります。

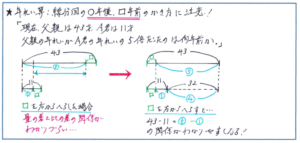
　上の図の右端から□年の部分をとってしまうと、父親とがＡ君の年れい差の32才が視覚的にわかりづらくなります。この場合、図の左端から○年後をとれば、32才の差がマル4にあたることが、とてもスムーズに把握できるようになるのです。
　落ち着いて考えれば線分図を見やすくかく方法が頭に浮かんできますが、時間に制限のあるテストになると、つい焦ってしまって右端から○年後をとってしまうという事態は起こりがちです。時間がない状況でも落ち着いて図がかけるように、普段から見やすい図をかく意識を強く持って演習を重ねるようにしましょう。

【第3位　円周上の点の移動：角速度を使った解き方を使いこなせていますか？】

　図形の辺の上を点が移動する問題では、例えば長方形の上であれば、点が移動する速さは「毎秒○cm」と、通常の速さの問題と同じ考え方で解き進めることができます。
　それでは次のような問題の場合、点の移動する速さをどのように表したらよいでしょうか。
　「中心をOとする円周120cmの円があります。点P、Qは円周上の点Aを出発し、どちらも右回りに動きます。点Pの速さが毎秒5cm、点Qの速さが毎秒3cmであるとき、三角形POQがはじめて正三角形になるのは出発してから何秒後ですか。」
　ここで「円周上の2点の間かくがはじめて24cmになるのは何秒後ですか。」という問題であれば、点Pの毎秒5cm、点Qの毎秒3cmをそのまま使うことができますが、2点の間の長さではなく、2点と円の中心を結んでできる角度が問題になっている場合、点が1秒間に何度進むのか、という「角速度」を使って解く必要があります。
　距離で表される速度（毎秒5cmなど）を角速度に変換する作業を、速く正確に行えるかどうかが、こうした問題での得点力に大きな差を生み出します。点Pは 円周を120÷5＝24(秒) で1周しますから、Pの角速度は 360÷24＝15(度/秒) と求まります。同様にQは 120÷3＝40(秒) で1周しますから、角速度は360÷40＝9(度/秒) と求まります。
　あとは三角形POQが正三角形になるケースですので、角POQが60度になるとき、つまり60÷(15－9)＝10（秒後）と正解に行き着くことができるのです。

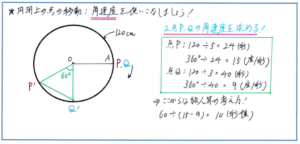
　円周上の点の移動に関する問題を解く際には、この角速度の考え方が必須になります。実際の入試問題でも、例えば「半径の違う円の円周上を点が移動する問題」といったかたちで角速度を使う解法が求められます。ぜひ角速度の考え方を身につけておきましょう。

【第2位　つるかめ算の応用：3量の関係を正しく2量の関係に変換できていますか？】

　基本的なつるかめ算は、2種類の単位あたりの量と、それらの個数、そして合計量がわかっているというパターンですが、応用パターンである「3種類の単位あたりの量と合計がわかっているつるかめ算」では、解き方に工夫が必要になります。こうしたタイプのつるかめ算を解く際のポイントは、問題文の条件を上手く使って基本的な2量のつるかめ算のかたちに直して考えることです。
　例えば、次のような問題。
　「1本の値段が240円、180円、120円の3種類のペンを合わせて22本買ったところ、代金は4440円になりました。240円のペンの本数が、120円のペンの本数の3倍とすると、240円のペンは何本買いましたか。」
　ペンが3種類のままではつるかめ算の考え方が使えなくなりますので、ペンの値段を2種類に直す必要があります。240円のペンの本数が120円のペンの本数の3倍になっていることから、「240円のペン3冊と120円のペン1本を1組として、平均の値段で考える」ことができます。(240×3＋120×1)÷(3＋1)＝210(円)と計算することで、240円、120円という2種類の金額を210円にまとめることができるのです。

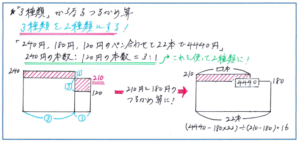
　こうして条件を整理すると、はじめの問題文から、「1本210円と180円の2種類のペンを合わせて22冊買ったところ、代金は4440円になりました。」と、基本的なつるかめ算のかたちに変換することができました。
　210円のペンの本数は、(4440－180×22)÷(210－180)＝16(本)となります。これは、120円のペンの本数を1とすると210円のペンの本数3の割合で合わせた本数ですので、210円のペンの本数は、16÷(3＋1)×3＝12(本)と求められます。
　3種類の量を2種類とする際、またつるかめ算の基本パターンを解く際でも、面積図の活用方法を覚えておくと、確実にミスを減らすことができます。これまでも多くの場面で使ってきた面積図はこれからも重要な解法ツールになりますので、図のかき方に曖昧な部分がある場合は、早めに復習をしておきましょう。

【第1位　回転移動：図をかいて回転する図形の位置関係は図をかいて把握しましょう！】

　回転移動の問題では、自分で図をかいて、その図から解答に必要な部分を正確に読み取ることが重要です。図を何度もかいて、図から何が読み取れるかを考える練習を重ねて行きましょう。
　特に図形のまわりを別の図形が回転するタイプの問題は頻出でありながら、全体正答率がなかなか上がらないケースが多く、得点ができればテスト結果に大きな差をつけられます。
　例えば正方形の辺上を長方形が回転移動する問題。ここでのポイントは正方形の頂点の部分でどのように長方形が回転するのかを把握することにあります。下の図のように、対角線の移動ではなく、長方形の1辺の回転移動を考えると、図の点Bが180度回転することがわかりやすくなります。
　また、回転する図形の頂点に正確に記号を入れることは、問題を解くうえでの大前提になります。この記号の書き入れを頭の中だけで行おうとすると、ミスが起きやすくなり、頂点が移動する様子を誤ってとらえてしまうことになります。だからといってじっくり時間をかけていては制限時間内に解ききることができない。そこで、記号の書き入れについて、時計と反対回りのルールを適用してみましょう。
　図のように、長方形の頂点記号が、時計と反対回りにA、B、C、Dと付されていますので、回転した後の図形も、当然その順番に記号が付されています。あとは回転の中心にあたる頂点にさえ着目しておけば、時計と反対回りに順番に記号を付して行けばよいのです。

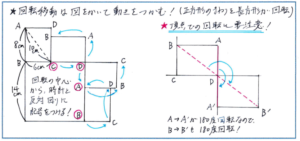
　図形の回転移動は、例えば四角形であれば、4つの点、4つの辺がまとめて動くように、ダイナミックな動きを見せるため、その動きの把握に難しさを感じられるかもしれません。ただ、上述の対角線の動きのように、動く部分をピンポイントに限定された部分に置き換えてみるとイメージがしやすくなりますし、点の位置さえ正確にとらえられていれば、移動の全体像をつかむことは決して難しくありません。移動のダイナミックさに惑わされないように、解法の手順をしっかり復習しておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。