メールマガジン宝箱 Mail magazine

　6年生になって最初の組分けテストです！新学年のカリキュラムに慣れるうえで大事な時期でもありますが、まずは最初の組分けでクラスアップを実現して、弾みをつけたいところです。そこで第1回組分けテストの対策ポイントを第5位から第1位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！
　さらに、このランキングを実践的に身につけられるように予想問題を作っていますので、予想問題も併せてご活用ください！ショートバージョンは、こちらから無料でダウンロード頂けます！

【第5位　曜日の問題：カレンダーを書いて解く方法も覚えておきましょう！】

　数と規則性の中でも「曜日」に関する問題は苦手とするお子様が多い単元のひとつです。問題の出され方としては限られており、問題文自体は複雑ではないのですが、月によって30日か31日か（あるいは28日か29日か）という場合分けが必要になり、問題によっては日数計算の際に「その日を含むかどうか」といった点にまで考慮しなければならないと、想定よりも処理しなければならない情報が多い点が、問題を難しく感じさせているのかもしれません。
　そんな中で例えば次のような問題では、図の使い方がポイントとなります。
「ある年の3月の金曜日の日づけの合計は58でした。この月の第1日曜日は3月何日ですか。」
　予習シリーズでは線分図を使って日数の関係を整理しており、この解法はまずしっかりと復習しておく必要があります。そのうえで、線分図ではなくカレンダーを使った解き方もありますのでご紹介しておきます。基本的な考え方は線分図と変わりませんが、○を使うことで日にちの関係が整理しやすいメリットがあります。
　まずカレンダーを作りますが、あくまで簡単に、ここで時間をかけてしまっては本末転倒ですので、枠の線もなしの簡略化したかたちとしましょう。そのうえで問題になっている金曜日のうち、第1金曜日を○とします。この後に○の中に数字を入れますので、○は少し大きめにしておきましょう。
　第1金曜日を○とすると、第2金曜日は○＋7、第3金曜日は○＋14、として、第5金曜日の○＋28まで書き込んでおきます。次にこの4月の金曜日が4週か5週かを決めるために、数字の部分の和を求めます。この数字の和が問題で出された数の和（今回であれば58）を超えていればこの月は第4週まで、超えていなければ第5週まで、と判断できます。7＋14＋21＋28＝70ですので、この月の金曜日は第4週までとなります。後は、○＋(○＋7)＋(○＋14)＋(○＋21)＝○×4＋42＝58より、○×4＝16から○＝4となり、第1金曜日は3月4日とわかります。ここでカレンダーの○の中に4と書き入れておきましょう。最後にカレンダー上の日づけを数えれば、第1日曜日は3月6日と求められます。

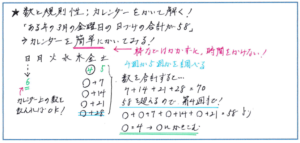
　カレンダーを使って解く場合、最後の第1日曜日が何日であるかのチェックもそのままカレンダー上の数字を追うことで済ませられます。図を使った解き方は少しでも多く持っておくと、問題内容によって対応できる幅が広がってきます。自分にとって使いやすい図がどれかも考えながら、図を使った解き方を固めておきましょう。

【第4位　やりとり算：線分図への書き込みを正確に行えていますか？】

　今回の組分けテストでの文章題の問題は、線分図で内容を整理する力が求められます。問題によって線分図のかき方が変わってきますので、どのように図をかいたらよいかを意識しながら復習をしておくようにしましょう。
　例えば次のような、やりとり算の問題。「ABCの3人が遊園地に行きました。Aは3人分の交通費、Bは3人分の入園料を、Cは3人分の昼食代を払いました。昼食代は、交通費と入園料の合計と同じです。AがCに900円、BがCに750円払うと、3人が払った金額が同じになります。1人分の昼食代は何円ですか。」
　やりとり算の典型的なタイプの問題で、線分図さえ正確にかければ正解にスムーズに行き着くことができます。Aが払った3人分の交通費を実線、Cに払った900円の部分を点線、同じようにBの払った金額も実線と点線を交えて作図します。やりとり後に等しくなった金額の線を縦に引き、Cがその線から900＋750＝1650（円）分長くなるようにすることで、最初の段階は完成します。ポイントはこの後、昼食代が交通費と入園料の合計と同じになるという内容を図にしっかり書き込むことです。この内容を見た目と頭の中だけで処理して計算に進もうとすると、思わぬ数の見落としが起こりかねません。下の図のように昼食代を表す線分図の下に入園料と交通費の合計を書き込むことを徹底しましょう。そうすることで、3人分の交通費が750＋900＋750＝2400（円）であることが一目でわかるようになるのです。あとは、3人分の昼食代が2400＋(2400＋900－750)＝4950（円）より、1人分の昼食代は、4950÷3＝1650（円）と求められます。

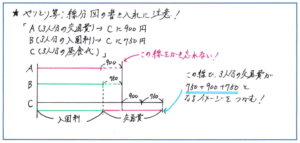
　今回のテスト範囲となる文章題はここで触れたやりとり算以外にも和差算や分配算などそれぞれに応じた線分図で解き進める問題が多くあります。予習シリーズで解説されている図の部分について、その成り立ちまで理解できるように、しっかり見直しておくようにしましょう。

【第3位　平面図形：図形の中から二等辺三角形を見つけ出せていますか？】

　平面図形の中でも角度の問題は、テストの前半の小問集合で出されることが多く、確実に得点をしたいところです。特に二等辺三角形は様々な図形との組み合わせで使われることが多く、「底角の大きさが等しい」という二等辺三角形の性質を的確に使いこなす必要があります。
　その中でも、円・おうぎ形と二等辺三角形の組み合わせには注意しましょう。円・おうぎ形の半径が同じ長さになることを利用して、図形の中に二等辺三角形が含まれるケースがテストでも頻出です。図形の問題でも「辺ABと辺BCの長さが等しい」と問題文の中で説明している場合であれば二等辺三角形や正三角形がすぐに見つかるのですが、円・おうぎ形の中に三角形が含まれる場合には、辺の長さが同じになることについての説明がありません。前提となっている「半径どうしが同じ長さになること」を自分で見つけ出す必要があるのです。特に三角形の向きが変わった場合に、二等辺三角形が見つけづらくなります。テストの際にテスト用紙を回転しなくても三角形が見つけられるようになるために、図形の中から「同じ長さ・同じ角度」を見つけ出す意識を持って問題に臨むようにしましょう。

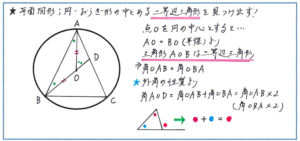
　また、三角形の外角の性質も使いこなせるように練習を重ねておきましょう。外角の性質は使わなければ角度が求められないものではありません。三角形の角度を順に求めて行くことで正解にたどりつけるのですが、この外角の性質を使いこなせれば、問題の時間を格段に短くすることができるだけでなく、計算自体を少なくできますので、ミスによる失点を防ぐ効果もあるのです。外角の性質も常に意識しておくようにしましょう。

【第2位　差集め算：数の差を的確に利用できていますか？】

　文章題の中で差集め算の問題はテスト中盤に出されることが多く、得点できるかどうかがテスト全体の偏差値にも大きく影響を及ぼすものです。特に予定と逆に品物を買うタイプの問題は内容のイメージが理解しづらい点もあって、難しく感じられることが多くあります。
　例えば「4人用の長いすと6人用の長いすをそれぞれ何脚か用意したところ、20人が座れませんでした。そこで、4人用の長いすと6人用の長いすの数を逆にしたところ、席が12人分あまりました。はじめに4人用の長いすと6人用の長いすは、どちらが何脚多かったですか。」と言った問題を例にしてみましょう。
　問題の内容は品物の数の取り違えではなく長いすの数の交換ですが、数を取り違えるという点で基本的な考え方は変わりません。まずはどちらの長いすの数が多いのかという点ですが、ここで間違えてしまうと先に進めませんので、解き方をしっかりと確認しておきましょう。
　このどちらが多いかという点は図ではなかなか解決できない、図をかく前段階の問題になります。長いすに座れない人が出る場合と、あまる席ができる場合でどちらの方が長いすに座る人数が増えたかを考えれば、明らかにあまる席ができる場合ですので、はじめは4人用の長いすが多かったことがわかります。この内容を、例えばはじめの4人用の長いすの数を○脚、6人用の長いすの数を□脚として、○×4＋□×6＋20＝□×4＋○×6－12の式を立て、両辺から同じ数値を引くことで、□×2＋20＝○×2－12の式とすれば○の値の方が大きい、つまりはじめは4人用の長いすが多かった、と判明するのですが、この式を使った解法は数学的な要素が強く、中学受験生のお子様にとっては理解が難しい可能性が高いです。式のかたちではなく、問題文を注意深く読み取って量の関係がつかめるように練習をしておきましょう。

　はじめの4人用の長いすが何脚多かったかを解くためには、図での整理が不可欠です。ただし、長いすの問題だからと言って、長いすの形まで書き込む必要はありません。重要なのは人数ですので、1脚あたりの人数を○を使って表せば内容は十分に整理できます。予習シリーズにも同じような図がありますが、この図を短時間でかき上げることがテストでは大きな効果を発揮します。ポイントを絞った図のかき方をしっかり練習しておきましょう。
　上下の図を見比べることで、長いすの数が多い分の人数の差（20＋12）が、1脚あたりの人数の差（6－4）が集まった結果とわかりますので、あとは(20＋12)÷(6－4)＝16より、4人用の長いすが16脚多かったと求められます。
　図で内容を整理すれば正確に解き進められるものの、頭の中だけで解こうとすると思わぬミスを起こしてしまうタイプの典型の問題と言えますので、図のかき方をしっかり復習しておきましょう。

【第1位　平面図形：面積比と底辺の長さの比の関係を正確につかめていますか？】

　平面図形の面積比について、「高さが等しい三角形の面積の比は、底辺の長さの比と等しい」という性質は、5年の後期に学習しましたが、6年になると、それを応用した形が多く出題されるようになります。
　下の（図1）のような三角形を内部の直線で同じ面積に分ける問題は頻出ですので、問題を見た瞬間に底辺の長さの比を利用することを思いつくようにまで、問題を見慣れるくらいに練習をしておきましょう。
　また、このタイプの問題は底辺の位置が水平ではないケースがほとんどですが、テストの際に問題用紙を回したりせずに、底辺が水平な位置になくても対応できるようになっておくことが、問題を解くスピードのアップにつながります。比の値を図に書き込む際には、数字だけを書き込んでしまうと、比の関係が正確につかめなくなってしまいます。数字だけではなく、○や△といった記号に数字を書き入れたかたちで、比の違いを視覚的にもつかめるようにしておきましょう。
　（図2）の面積比のパターンも覚えられているかどうかで得点力に大きな差が生まれる問題になります。このタイプの問題も（図1）の際と同じように、底辺の位置が水平ではないことが多くなります。まずは底辺が水平の基本パターンを確実に覚え込んだうえで、底辺の位置が変わっても対応できるようにしておきましょう。

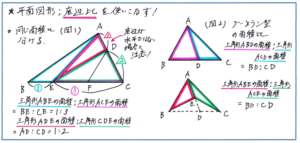
　平面図形の中でも面積比の問題は、解き方を多く持っておくことが大きな得点差を生み出すポイントになります。問題を見てできるだけ短い時間で解き方が思い浮かべられるように、解き方を多く持ち、それぞれの解き方を確実に使いこなせるように、復習を徹底的に重ねておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。