メールマガジン宝箱 Mail magazine

　4月マンスリーテストはちょっと厄介なテストです。と言いますのは、春期講習で演習した割合や平面図形、立体図形などの重要単元に加え、さらには速さも含まれるといった範囲の広いテストで、どこから復習を進めればよいか迷ってしまうテストだからです。とは言え、ポイントをしっかり絞れば、クラスアップのチャンスは十あります。そこで4月度マンスリーテストの対策ポイントを第5位から第1位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！
　さらに、このランキングを実践的に身につけられるように予想問題を作っていますので、予想問題も併せてご活用ください！ショートバージョンは、こちらから無料でダウンロード頂けます！

【第5位　立体図形の問題：覚えておくべき基本パターンを確実におさええられていますか？】

　立体図形の中で、暗記しておくべき基本パターンを使いこなせるかどうかで、テスト前半の図形の小問集合の問題での正答率に大きな差が生まれてしまいます。問題を見て、すぐに解法を浮かべられるようにしておく必要がありますし、それ以前に、基本パターンを覚えられていないと、解くことができないような問題があることもおさえておかなければなりません。
　特に、立方体のカドにできる三角すいの展開図が正方形になるパターンは、塾でも自明のこととして詳しく説明してくれないことがありますので、知識として覚えられているかどうか確認しておきましょう。　
　問題としては、三角すいを底面の直角二等辺三角形が水平になるように立てた際の斜めになっている面（以下、斜面とします）の面積を求めさせるだけでなく、この斜面を底面とした場合の三角すいの高さを求めさせるものもあります。いずれにしても、斜面の面積を求めることには変わりはなく、そこで三角すいの展開図が正方形になる「知識」を活用します。

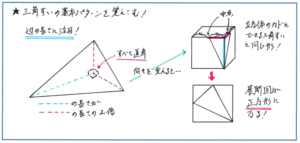
　このタイプの問題は、三角すいが直角二等辺三角形を底面とするような立ち方をしていれば、すぐに展開図が浮かびますが、立体の向きが少しでも変わると、どう解き進めてよいのか迷ってしまうことが多くあります。図形の形で覚えるのではなく、直角二等辺三角形の等辺の長さと、それに垂直な直線の長さが1：2の関係にある場合に、展開図が正方形になることを覚えておきましょう。視点の切り替えができれば、難問にも対応できるようになります。

【第4位　場合の数：解き方を複数持っていると、難しい問題が断然解きやすくなります！】

　場合の数の問題では、問題内容に応じた解き方のパターンを覚えておけば、テストで解答にかける時間を一気に短縮でき、正解できる可能性がグンと高くなります。
　ただ、問題の内容が複雑になったり、あてはまる場合の数が多くなった場合には、そうしたパターンにあてはめることが必ずしも有効ではなくなってしまいます。
　その端的な例が「最短経路」の問題です。マス目で示された道の、端から端まで最短経路で行く方法を求めるタイプの問題ですが、。このタイプの問題では、まずマス目の端に数字を書き込んで、その和を書き連ねて行く解法が浮かんでくるでしょう。この解法は、計算を機械的に、スピード感をもって進められるメリットがありますので、答えとなる場合の数が少ないケースでは有効です。
　ところが、最終的な答えが3ケタ以上の数になってくると、計算の過程でミスが起きやすくなってしまいます。このパターンの問題は、途中で1つでも計算ミスをしてしまうと、そこから間違いが連動してしまいますので、細かな計算ミスは何としても防がなくてはなりません。ただ、計算の工夫などはできませんので、とにかく正確に解く、ということに尽きてしまいます。
　そこで、別の解法を考えてみましょう。下の図のようなマス目の場合、A地点からB地点まで最短経路で行くには、マス目の辺を横に4個、縦に6個、合計して10個の辺を進めばよいことになります。ここから、10個の辺のうち4個を横の辺にする、という点で、「10個の辺から4個の辺を選ぶ選び方」と考えられるのです。こうなれば、計算は、10×9×8×7/4×3×2×1の式で進められます。この分数式では約分ができる数の組み合わせがありますので、結果、10×7×3＝210と、難度の低い計算で正解まで行き着けるのです。

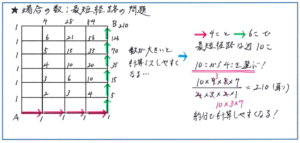
　まずは基本パターン（今回であればマス目に書き込む方法）をしっかり覚え、計算ミスが起きやすいケースと感じられた際には、別の解法（今回であれば選び方の方法）を使う、という判断ができるように、解法を少しでも多く持っておきましょう。

【第3位　立体図形：回転体の問題でどの長さが必要になるか把握できていますか？】

　立体図形のうち、回転体の問題では、回転する平面が、回転軸から離れたところにあるパターンに注意する必要があります。回転してできる立体が、底面がドーナツ型の円柱になることはイメージできるかと思いますが、問題は半径にあたる長さです。
　例えば図のような立方体について、上下の正方形の対角線の交点を結んだ軸で回転させた場合の、面ABFEが通った部分の体積を求める場合で考えてみましょう。

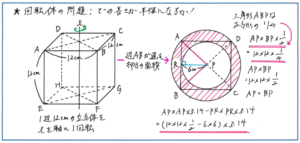
　回転してできる立体の高さは12cmとなります。ポイントは底面積ですが、ここでは「点Pを中心として1回転したときの、辺ABが通った部分の面積」となります。その面積は、Pから最も遠い点とPを結んだ線を半径とする大きな円と、Pから最も近い点とPを結んだ線を半径とする小さな円との間にできる部分、つまり、真ん中が空いたドーナツ型になります。ここで、Pから最も遠い点がA（またはB）になることは容易に理解できますが、問題はPから最も近い点がどこかです。ここでは、PからABに垂線を下して、ABとの交点をRとした場合に、そのRが最も近い点になります。
　ここからは2つの半径、APとPRの長さが必要になりますが、PRについては、12÷2＝6（cm）と、すぐに求められるでしょう。ポイントはAPの長さですが、小学生の段階ではこのAPの長さを計算で求めることはできません。
　ただし、今回はAPを半径とする円の面積を求めるので、AP×APの値がわかればよいことになります。この半径の長さが分からなくても、半径×半径の値を求めるという解法は、このタイプの問題に限らず、円やおうぎ形の問題では頻出ですので、しっかりおさえておきましょう。
　ここで三角形ABPに注目してみます。この直角二等辺三角形の面積はAP×AP÷2で求められます。また三角形ABPの面積は、ABを1辺とする正方形の4分の1になります。正方形の面積は、12×12ですので、12×12÷4＝AP×AP÷2より、AP×APの値を、12×12÷2と求められます。
よって、求める底面積は、12×12÷2×3.14－6×6×3.14＝(12－6)×6×3.14＝36×3.14＝113.04（平方cm）となります。3.14計算をまとめることにも注意しておきましょう。
　このドーナツ型の面積の求め方も、第5位でご紹介した基本パターンと同じく、解き方を知識として暗記しておけば、あとは計算ミスがないように集中して解き進めることができます。

【第2位　速さのグラフ：速さと時間の逆比の関係をグラフから正確に読み取れていますか？】

　6年生になると速さの問題の難度が大きくアップしてきます。その要因は比と関連づけた問題が増えてくることにあります。特に「逆比」の考え方を確実に理解し、使いこなせれるようになれば、テストの終盤にある応用問題でも正解できるチャンスが大きく広がってきます。
　進む距離が同じであれば、速さと時間が逆比の関係にあることは、速さと比の基本であり、例えば「駅から公園まで春子さんは45分、秋子さんは75分で進みました。春子さんと秋子さんの速さの比を求めなさい。」といった基本問題であれば、1/45：1/75＝5：3と、時間をかけずに速さの比を算出できるでしょう。ポイントとなるのは、逆比の関係を問題文、特にグラフの中からいかに速く的確に見つけ出すか、ということです。
　下のグラフは、「家を10時に出発した弟を、10時15分に家を出た兄が追いかけ、10時35分に追いつき、同じ速さで家に戻ってくる」といった様子を表したものです。このグラフの中で兄と弟の進んだ距離が同じところは、もちろん家から兄が弟に追いついた地点までの距離（図の★部分）です。この距離を弟が進むのにかかった時間は、10時35分－10時＝35分、兄が進むのにかかった時間は、10時35分－10時15分＝20分とわかります。ここから兄と弟の速さの比は、1/20：1/35＝7：4と求められます。

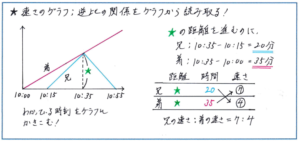
　ポイントは、グラフの縦の部分が距離を、横の部分が時間を表すことを踏まえて、進んだ距離とそれにかかった時間がグラフのどの部分にあたるのかを正確に把握すること、そのために、わかっている数値はどんどんグラフに書き込んで行くことです。
　これから速さのグラフは加速度的に複雑になって行きます。その際に、グラフのある部分に注目して、そこで今回のように逆比の関係に気づくことができれば、難問を攻略する武器を手にすることができます。普段の演習でも、速さのグラフでどの部分が何を表しているのか、注意深く見るようにしましょう。

【第1位　平面図形：有効な補助線を引くことはできていますか？】

　平面図形の面積比の問題では、有効な補助線を引くことが求められるケースが増えてきます。
　例えば、図のように三角形ABCの辺ABを4：3に分ける点をF、辺BCを5：3に分ける点をDとします。辺AC上に点Eをとって、点Eと点F、点Eと点Dをそれぞれ結んで、三角形AEFの面積が36平方cm、三角形CDEの面積が42平方cmとなったときの、四角形BDEFの面積について考えます。

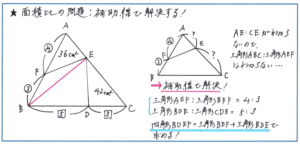
　図形を見て、三角形の二辺上の点を結んだ際の、辺の長さの比のかけ合わせで、小さい三角形の面積を求める解法が浮かぶかもしれません。それによって三角形ABCの面積がわかれば、そこから三角形AEFと三角形CDEの面積を引くことで四角形BDEFの面積は求められるのですが、AE：CEの比がわかっていませんので、この解法はここでは活用できません。
　そこで、三角形ABCを求めるのではなく、四角形BDEFを2つに分けて求める方針で解き進めてみましょう。点Bと点Eを結んで、四角形BDEFを三角形BEFと三角形BDEに分けます。次に三角形ABEに注目すると、ここに高さを共通する2つの三角形が並び接していることがわかります。三角形AEFと三角形BEFは高さ共通ですので、その面積比は底辺の長さの比と同じ、という解法が使えるのです。
　つまり、三角形AEF：三角形BEF＝AF：BF＝4：3、同じく三角形BDE：三角形CDE＝BD：CD＝5：3となります。ここから、三角形BEFの面積が、36×3/4＝27（平方cm）、三角形BDEの面積が、42×5/3＝70（平方cm）となり、四角形BDEFの面積が、27＋70＝97（平方cm）と求められます。
　これからテストで出される平面図形の問題は、ただ与えられた図形を見ただけで解けるものは大きく減ってきます。補助線を引いて、視点を切り替えることで、これまでに覚えてきた解法を使う必要が出てくるのです。問題に応じて解法を正確に、少しでも速く使うためには、面積比の基本パターンをしっかり頭の中に植え付けておかなくてはなりません。典型的な図形を何度も見直してうえで、テキストで解くのに時間がかかってしまった問題について、どのような流れで解いたのかを重点的に見直しておくようにしましょう。図形に慣れることが解法を使いこなすためには不可欠になります。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。