メールマガジン宝箱 Mail magazine

　テスト範囲が広い上に旅人算や立体図形が含まれる、手ごわいマンスリーテストです。各単元で習う解法を、速く的確に使いこなせるかどうかが勝負の分かれ目になります。クラスアップのチャンスを逃さないためにも、解法をどれだけ吸収できているかテスト前にしっかり確認しておきたいところです。そこで4月度マンスリーテストの対策ポイントを第5位から第1位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！
　さらに、このランキングを実践的に身につけられるように予想問題を作っていますので、予想問題も併せてご活用ください！ショートバージョンは、こちらから無料でダウンロード頂けます！

【第5位　計算問題：分配法則は確実に使いこなせていますか？】

　テストで高得点を取るための必須条件は、計算問題を少しでも早く正確に解くことであることは言うまでもありません。その計算問題も、テストを重ねるごとに難度が高くなってきます。確実に得点を重ねられるかどうかは、計算の工夫、特に「分配法則」を使いこなせるかどうかにかかっています。
　例えば、24×17＋24×33のように、共通する数字が見てすぐわかる場合であれば、24×(17＋33)と、楽に計算を進められますが、一見したところ共通していない数字の組み合わせを、加工することで分配法則を使えるかたちに持ち込む力が求められる問題も、これからは多くなってきます。例えば下のような、375で構成される点では共通しているものの小数の位が異なる数でつくられた式の場合、どのように対応すればよいでしょうか。式を構成する3つの項に、375、3.75、0.375とありますので、このどれかに他を合わせるかたちで加工をして行きます。ここで整数である375に統一すると楽に見えますが、掛け合わせの相手が0.007でやりづらさが残ります。そこで、0.375という数字に注目してみましょう。

　計算の工夫の基本、分数と小数の置き換えで、0.125＝1/8のシリーズで、0.375＝1/8があります。これを利用して、0.375に統一する方法があるのです。しかも最も小さい0.375に合わせることで、かけ合わせた数を大きくできるというメリット（小さくするより計算ミスがしづらくなる）もあります。0.375に統一すべく数を調整し、そのうえで分配法則を利用してみると、結果として計算が圧倒的に楽になることがわかります。
　テスト全体の難度が上がれば上がるほど、計算問題での得点の重要性が増してきます。ただ計算演習をくり返すのではなく、ミスを減らすための計算の工夫がテストの際に落ち着いてできるよう、普段から意識して練習を重ねましょう。

【第4位　分数：通分の応用パターンの問題をミスなく解けるような対策はできていますか？】

　分数の問題には様々なタイプがありますが、特に確実に得点源としておきたいのが、通分の応用パターンの問題です。ポイントは2点あります。
　まず1点は、分子や分母が小数になることにためらわないこと、そして計算ミスをしないように十分に注意することです。このタイプの問題での小数計算は、割り切れないケースが多くあります。その際に延々と計算を続けるのではなく、小数第2位くらいまでで計算を切り上げることを含め、とにかく速く、間違いなく計算をするように徹底注意しましょう。
　もう1点は数の大小関係です。例えば下の問題のように、計算の結果、分子が72より大きく73.5より小さいとなった際に、あてはまる数が73であることは、瞬時に対応しなければなりません。特に「より大きい（より小さい）」と「以上（以下）」の区別を徹底し、細かなミスを起こさないように十分に注意しましょう。当たり前のように見えて、テストになると、こうした大小関係で思わぬミスを起こしてしまうことがあります。時間がない状況でも、確実に正解にたどりつけるように、細かなミスを回避することに注意して演習を重ねておきましょう。

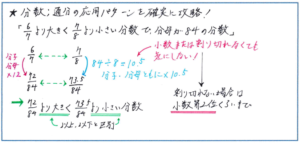
　今回の範囲の広いテストの中でも、この問題を含めた分数・小数の単元は偏差値の分かれ目になる可能性がとても高くあります。この通分応用パターン以外にも、循環小数など、確実な計算力が大前提となる問題ばかりですので、自分の計算での誤答パターンをしっかり確認して、テストに少しでも落ち着いて臨めるように、理解度を整理しておきましょう。

【第3位　消去算：代入法で時間を短縮できる方法を習得できていますか？】

　今回のテスト範囲には、つるかめ算や過不足算といった和と差に関する問題が含まれます。どの単元も解き方をしっかり身につけられていれば、比較的得点のしやすい問題になるでしょう。それだけに、テスト後半で出される難問にかける時間を作り出せるように、この単元で少しでも時間を短縮できる解法を身につけておきたいところです。
　例えば消去算の代入法を使ったタイプの問題で、式の立て方ひとつでかかる時間に大きな差が生まれることがあります。「商品Aを3個と商品Bを7個買うと2050円で、商品Bは商品Aよりも50円安いです。商品Bの代金は何円ですか。」といった問題を例に考えてみましょう。（商品A×3）＋（商品B×7）＝2050円、の式は迷いなく立てられるかと思いますが、ポイントは2つ目の式です。問題文に書かれたままに、「商品B＝商品A－50円」、としてしまいたくなりますが、求める代金は商品Bですので、「式を商品Bのみで表す」というかたちの方がより有効です。そのためには商品Aを商品Bに置き換えなければならず、問題文の2つめの条件を「商品A＝」という式にしなければなりません。ここで問題文を見てすぐに式を立てられればよいのですが、少しでも迷うようであれば、日本語の置き換えをしてみましょう。つまり、「商品Bは商品Aよりも50円安い」を「商品Aは商品Bより50円高い」と置き換えれば、容易に式が立てられます。
　問題文の表現の通りに「商品B＝商品A－50円」のままで式を解き進めてしまうと、商品Aの代金を求めたうえで、さらに最後に商品Bの代金を求める、というひと手間が増えてしまうのです。

　ほんのひと手間のように見えますが、先に触れました通り、この単元の問題で重要なのは時間をできるだけ短縮することです。問題文のままに式を立てるのではなく、求めたいものは何か、そのためにはどのような式を立てれば近道になるのか、という発想を持てるように、普段の演習から気をつけておくようにしましょう。

【第2位　平面図形：図形の回転移動で点の動きを正確に読み取れていますか？】

　三角形などの平面図形が直線上や他の図形の辺上を回転移動する問題では、単純に直線上を移動するのではなく、折れ線や多角形の辺上を移動するような応用問題が、今回のマンスリーで出される可能性が高くあります。
　移動するのが直線上でも折れ線や多角形の辺上であろうと、基本的な考え方に違いはありません。移動する図形の頂点記号を書き込むことで、どのような回転がなされているのかを把握するのが基本の取り組みです。
　図形の回転移動では、点はおうぎ形の弧を描いて移動しますが、中心角が何度の弧であるかを見逃さないようにしなければなりません。この点が単純な直線上の移動と、複雑な図形上の移動との大きな違いになります。例えば下の図のような、90度に折れ曲がった線の内部を正三角形が回転移動するケースでは、折れ曲がった部分での回転の様子を的確につかむことがポイントとなります。この部分でのおうぎ形の中心角が30度になることは、このタイプの問題を数多く解いた6年生であればすぐに答えられるものですが、まだ習いかけの段階ではなかなかイメージが難しいかもしれません。このイメージを、想像ではなく具体的なものとするためには、まずは自分で図をかいてみましょう。手間はかかりますが、手を動かし、できる限り正確に図をかくこと、特に、点が三角形の頂点を通ることをしっかり意識して図をかけば、イメージは頭の中に深く植え付けられ、点が移動する様子が驚くくらいに速く頭の中に浮かんできます。

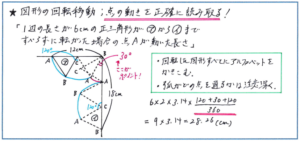
　回転移動に限らず、平面図形の難問は慣れがあるかないかが得点の分かれ目になります。ただ漫然と演習をするのではなく、点が移動する様子などを細かく正確に追う、といったプロセスを重ねることが、正解につながる正しいイメージづくりをするためには不可欠なのです。

【第1位　旅人算：状況を把握するための図は正確にかけていますか？】

　旅人算の問題では、動きを正確に把握するための図のかき方がポイントになることは言うまでもありませんが、その動きが複雑になった際にも、正しい解法を導き出すような図のかき方が得点差を生む要素になります。まずは基本パターンの問題への対応の仕方をしっかり固めることがこの時期のマンスリーでは重要になります。
　基本パターンのひとつに挙げられるのが、折り返しの問題です。例えば「A君は分速90m、B君は分速60mでP地点を同時に出発し、1500m離れたQ地点に向かいました。A君がQ地点に着くとすぐに引き返すとき、A君とB君はP地点から何m離れた地点で出会いますか。」といった問題で、図のかき方を確認してみましょう。折り返し問題では、P、Q両地点を結ぶ線分図をかき、そこにより速く進むA君の動きをUターンのような矢印の線で引き、B君と出会うまでの線とします。この図をかくことで、2人が動いた距離の和が地点間の距離の2倍になることが、即座に把握できます。
　後は、最後に求める数値がどこなのかを間違わないようにしましょう。特に距離を求める際には、誰がどこからどこまで移動する距離なのか、最後の詰めの部分では、急がず一旦立ち止まって確かめる方がよいでしょう。

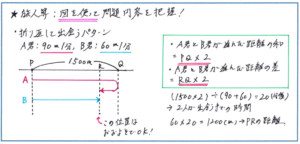
　ここで気をつけるのは、図をかく際には2人が出会う地点がどこになるかについて、細かく考えすぎないことです。まだわかっていない値について深追いすることは、時間の浪費にしかなりません。あくまでも2人が出会うまでの過程をつかむことが図をかく目的ですので、細かな数値に気をとられて時間をかけ過ぎて、せっかくの得点のチャンスを逃すことがないようにしましょう。この問題に限らず、速さの状況を再現する図をかく際には、明らかにわかっている大小関係以外は、おおまかで構わないという意識で臨みましょう。目的を達するために必要な情報以外は、細かな不確定要素を追い求め過ぎないことです。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。