メールマガジン宝箱 Mail magazine

　今回のマンスリーテストは、2量の関係でのタクシー料金タイプの問題や、立体図形の色づけ問題など、パターン化された解き方を確実に覚えられているかどうかで得点差が大きくついてしまう問題が多く範囲に含まれます。それらの解き方がしっかり頭の中に刷り込まれいるかどうか、テスト前にチェックしておきたいところです。そこで5月度マンスリーテストの対策ポイントを第5位から第1位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！
　さらに、このランキングを実践的に身につけられるように予想問題を作っていますので、予想問題も併せてご活用ください！ショートバージョンは、こちらから無料でダウンロード頂けます！

【第5位　平面図形：図形の折り返しでの着眼点をおさええられていますか？】

　平面図形の角度の問題の中で、図形を折り返すパターンがあります。このタイプの問題はテストの前半に出てくる、何としても得点しておきたい問題となることが多いので、着眼点を確実に整理しておきましょう。まずは同じ角度がどこに移動しているかをできるだけ早く見つけられるようにしておくこと。折り返しの基本の基本である、同じ角度の移動は、問題の難易度に関わらず見つけやすいケースが多いです。同じ角度の部分に同じ印をつけることで、見逃しがないようにしておく必要があります。次に意外と見過ごされがちなのが、錯角の関係を見つけ出すことです。特に長方形を折り返す際には、もともと平行な関係の辺が2組ありますので、これを利用した錯角の関係が図形の内部に隠れていることがあります。これを確実に見つけ出せば、同じ角度の関係をより多く見つけることにつながります。
　そのうえで三角形の相似の関係に気づくこと。折り返しの問題に限らず、6年生の平面図形においては真っ先に着目しなければならないのが相似の関係です。特に折り返しの問題では同じ角度の関係が生まれるので、相似の関係が生まれやすくなります。相似な図形の関係を見つけ出す際には、同じ角度の関係と、辺の長さの比が同じ関係を把握する必要がありますが、比の関係よりも同じ角度の関係は視覚的に見つけやすくなります。だからこそ、折り返しの問題での相似の関係は確実に見つけ出すことが求められますので、普段の演習で、同じ角度に印をつけるといった解き方の手順をしっかり意識しながら、図形を見る目を養っていきましょう。

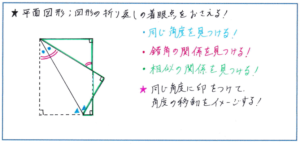
　平面図形の中でも角度の問題はテストでの全体正答率も高くなることが多く、テスト全体の偏差値を安定させるためには、着眼点を逃さずに図形に臨むことが必須となります。

【第4位　狂った時計の問題：「遅れる」「進む」を頭の中でなく図で整理する方法を覚えられていますか？】

　2量の関係の中で、狂った時計の問題では、図を使って解き進めることが短時間で正解に行き着くためのポイントになります。過不足算の「余る」「足りない」と同じように、この狂った時計の問題でも、言葉の持つ意味を間違いなくとらえられるかどうかが得点できるかどうかの分かれ目になります。言葉の問題と言っても国語の語彙とは違って、算数の場合は図で整理するといった対策方法があります。時計が「遅れる」「進む」と言った状況を、相似が利用できるような図にまとめれば、言葉に惑わされずに解法の方針を立てることができます。
　手順はいたってシンプルで、正しい時間を横の線として、遅れる、進むのどちらかを線の上下で示す、というルールで作図。後は問題で与えられた数値を書き入れて、相似な関係にある図形を見つけ出して、比の計算に持ち込めば、ほとんど問題は攻略できます。
　例えば、「ある日の朝7時の時報のときに時計は6時58分を指していました。その日の夕方、6時の時報のときに同じ時計を見たら6時3分を指していました。この時計が正確な時刻を指したのは何時何分ですか」といった問題があるとします。
　下の図のように正しい時間の流れを表す1本の横線をひき、左端を7：00、右端を18：00として、7：00の下に6：58、18：00の上に18：03をとって、6：58の点と18：03の点を結べば、横の線と斜めの線が交わる点では、時刻に差がないことから、時計が正しい時刻を表していることがわかります。
　あとは相似の考え方で解き進めば、正しい時刻の点は、18：00－7：00＝11：00を2：3に分ける点ですので、11×2/5＝4・2/5（時間）より、7：00＋4：24＝11：24と求めることができます。

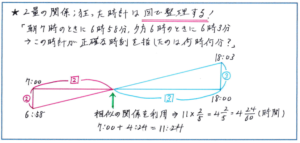
　言葉の意味を確実に把握できて解き方に慣れれば、無理に図を使わなくても正解に行き着くこともできますが、制限時間のあるテストでは、少しでも焦ってしまうと言葉の意味の取違いなどの、思わぬミスが起きてしまいます。確実に「遅れる」「進む」の概念が頭の中に刷り込まれるまでは、図を使って言葉の意味を視覚的にとらえる練習を重ねておきましょう。

【第3位　立体図形：複雑な立体の表面に色をつける問題で、段ごとに分ける解き方を使いこなせていますか？】

　立体図形のうち、複雑な成り立ちの立体の表面に色をつけて、それをばらばらにした際の色がついた面の数を求めるタイプの問題があります。立体図形そのものが、見えない部分があるために平面図形よりもイメージが難しいのですが、さらにこの色つけの問題では何面に色がつくのかまで考えねばならず、頭の中だけで解き進めるのはまさに至難の業となります。
　そこで必要となるのが、立体を段ごとに分けるといった解き方。これは授業でも解説されることがあるかと思われますが、段に分ける、ということまでは頭で理解できても、いざ自分でやろうとすると慣れないうちは思いのほか時間がかかってしまいます。解き方が理解できていれば、小問すべてがあっという間に解けるのが、未定着のままでは時間がかかって結果間違えてしまうという結果になりかねないタイプの問題の典型のひとつです。例えば正方形のかたちが少しゆがむなどの雑さは気にしなくて構いません。図の量が多くなりますので、自分が整理できる範囲の正確さでかけばよいので、手順を少しでも速く進められるように練習をしておくようにしましょう。

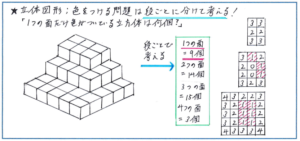
　図形の問題はつい与えられた図だけで解決しようとしてしまいがちですが、内容を整理するための図を自分でかき加えることが必要となる問題が、6年生のこれからの時期からはどんどんその数が増えていきます。ためらうことなく有効な図がかけるように、手を使うことを惜しまず、面倒がらずに図をかくという意識をいま一度強く持って問題演習に臨んでください。

【第2位　2量の関係：段階的に増加する量をグラフ以外の方法で解けていますか？】

　タクシー料金や荷物の運賃など、2量の関係が単純な比例関係ではなく、段階的に増加するようなタイプの問題では、もちろんグラフを使って解くこともできますが、該当する「範囲」を求められることが多く、その場合は必ずしもグラフを使う方法が解きやすいとは限りません。まずグラフをつくるのに手間がかかるうえに、求める範囲がどこにあたるのかを視覚的に把握するのが難しく感じられるケースがあります。
　そこでグラフは使わずに、「最長・最多とその前」の考え方で解く方法を考えてみましょう。例えば、「ある市のタクシー料金は、乗ってから1500mまでは620円で、1500mを超えると80円加算され、以後315mを超えるごとに80円加算されます。例えば2200m利用したときにかかる料金は860円です。A君がこのタクシーを利用したとき、支払った料金は1500円でした。A君がこのタクシーを利用した距離の範囲は何mを超えて何mまでですか。」といった問題。このタクシー料金の問題は出題されるパターンがある程度決まっていて、ほぼこの例題のようなかたちに集約されます。
　このタイプの問題を解くうえでのポイントのひとつは、例を有効に活用すること、つまり解き方を例で確かめるということです。この問題では、2200m利用した際の料金が860円であるという例、これを解法のチェックに使いましょう。
　860－620＝240（円）が基本料金を超えた分の料金。240÷80＝3より、860円で進める「最長」は1500＋315×3＝2445（m）、その「直前」の距離が2445－315＝2130（m）となり、2200mがこの区間に入っていることが確認できます。
　そこで同じように、(1500－620)÷80＝11より、11回の加算で、1500＋315×11＝4965（m）となりこれが最長、その直前は4965－315＝4650（m）となり、距離の範囲が4650mを超えて4965mまで、と求められます。

　これを1500＋315×10＝4650（m）を「最短」として、直後の範囲を4650＋315＝4965（m）とすることも、もちろんできます。いずれにしても、計算結果を最長や最短の値とすることで複雑な問題を解きほぐすことができます。このタイプの問題では、グラフに頼らない解法も身につけておくようにしましょう。

【第1位　立体図形：水位の変化で、解き方の工夫ができていますか？】

　立体図形の中でも、水位の変化は5年生の時から演習してきていますので、見かけの深さなど、基本的な解き方にはだいぶ慣れてきたでしょう。そこで、よりミスが起こりにくい解法を使えているかどうか、という点を確かめておきましょう。
　例えば、おもりを1個ずつ沈めていき、何個目を沈めた際に水があふれるか、といったタイプの問題。この場合、沈めるおもりの高さが低く、おもりすべてが水の中に沈み込むことが多くなりますので、水が入った部分ではなく、「水が入っていない部分」に注目することで、一気に解きやすくなります。もちろん考え方の根本には、見かけ上増えた水の量が水のなかった部分の体積を超える、といった「見かけ」の考え方がありますが、計算自体は水が入った部分で考えるよりも進めやすくなります。
　また、いま一度確認をしておきたいのが、水そうの中に高さのあるおもりや容器を沈めるタイプの問題で、水そうの断面図を使いこなせているかどうかです。その際に、下の図のように水そうの底面積を横の長さとした長方形を使うか、おもりの部分をのぞいた底面積を使うかについては、問題内容に合わせて判断できるようにしましょう。どちらを使っても、もちろん答えは変わりませんので、与えられた値をそのまま使える方を選んで解けばよいでしょう。

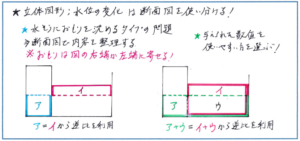
　どの問題でも断面図をかく必要があるわけではありません。ただし、逆比の考え方を習った段階になれば、断面図を使うことで、面積図のような考え方で水深変化の様子を具体的に把握することができます。ここでもやはり、断面図をかくことを面倒に思わずに作図に着手できるように、普段の演習から図の有効性を確かめながら練習を重ねていくようにしましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。