メールマガジン宝箱 Mail magazine

　今回のマンスリーはグラフを使った様々なタイプの問題がテスト範囲に含まれます。グラフは慣れてしまえば問題を解くヒントを多く与えてくれる、強力な武器となります。速さや図形の問題の中で出てくるグラフについて、その特徴をしっかりつかんでおけば難しい問題への対応力も大きくアップします。クラスアップのチャンスを逃さないためにもグラフを読み取るポイントはしっかりつかんでおきたいところです。そこで5月度マンスリーテストの対策ポイントを第5位から第1位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！
　さらに、このランキングを実践的に身につけられるように予想問題を作っていますので、予想問題も併せてご活用ください！ショートバージョンは、こちらから無料でダウンロード頂けます！

【第5位　規則性：数表の見方は確実にできていますか？】

　規則性の問題の中で、表の中に数字が並ぶ数表のタイプの問題では、数字が横並びになる数列タイプの問題とは違った注意点があります。
　まずは表の位置と数の性質の関係を的確につかむことが重要です。特にこのタイプの問題では、表のどちらかの端に「平方数（同じ数のかけ合わせ）」が示されることが多いので、この平方数をヒントとすることを徹底できるように、数字を見る目を鍛えておきましょう。例えば下の数表では、表の「1段目の奇数列目」に列の数字の平方数が、「偶数段目の1列目」に、段の数字の平方数が並んでいます。目印となるように平方数に○を付けておいてもよいでしょう。
　次に注意すべきは「数字が増える向き」です。数列タイプの問題では考える必要がないことですが、この数字の向きを間違えると、せっかく規則性を見つけ出しても正解に行き着くことができません。例えば下の数表では、数字の増える向きが、奇数段目では左から右に大きく、偶数段目では右から左に大きくと逆になります。正確に向きを把握するために、矢印を表にかき込んで視覚的にもイメージを固められるようにしてもよいでしょう。
　これらのポイントをおさえた上で、かき込みをフル活用して、数の並びの規則性を確実につかみとりましょう。例えば下の数表で「60が何段目の何列目の数か」を答える際には、まず60に近い平方数として、8×8＝64が8段目の1列目にあることに着目します。次に数字の増える向きが偶数段目では右から左に大きくなりますので、8段目は64から始まって、63、62、61、60と数が減って行きますので、求める答えは、「8段目の5列目」となります。最終的な答えに行き着いた際には、段や列を取り違える（5段目の8列目としてしまう）といったミスがないように注意してください。

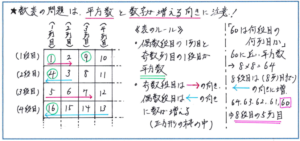
　規則性の問題では、数を書き出せば正解に行き着くことも多くあります。今回の問題でも60までであれば書き出すこともできますが、これが360など大きな数になった際には、とても時間内に対応することができなくなります。規則を見つけ出して計算で解答を進める習慣を身につけておくようにしましょう。

【第4位　水量グラフ：仕切りのある問題では断面図を使いこなしましょう！】

　立体図形の中で、容器の水深の変化と、その様子を表したグラフの問題は、今回のマンスリーテストの中でも得点差がつきやすい単元となります。容器の中で水深がどのように増えるかをつかむだけでなく、それがグラフにどのように表されているかも把握しなくてはならず、時間がかかる上にグラフの見方が少しずれてしまうだけで正解への道が閉ざされてしまう要注意の単元なのです。
　こうした問題で確実に正解を手にするためには、断面図の利用が有効な手段となります。特に容器に仕切りが入ったタイプの問題では、容器の断面図を見ることで、容器に水が入る場所を区分けして詳しく変化の様子をつかめるようになります。
さらに下のように、断面図とグラフを横並びにできれば、グラフのどの値が容器のどの部分にあたるのかが一目のうちにわかります。そして断面図の区分けされた部分の記号をグラフにかき込めば、容器の場所とグラフを対応することができ、変化の様子がより見やすくなります。

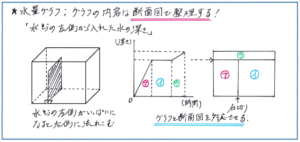
　断面図をかくことも、グラフへの書き入れをすることも手間はかかりますが、難度の高い問題で確実に得点をするためには、必要な手間と言えます。その作業をできるだけ短い時間で進められるように、普段から有効な手間をかける習慣をつけておくようにしましょう。

【第3位　点の移動：底辺の長さと面積の関係を正確に理解できていますか？】

　点が一定の速さで三角形や四角形の辺上を動くタイプの問題は、速さと面積が複合された問題になります。面積の変化をどれだけ正確に把握できるかが得点の分かれ目になります。特に、「面積が三角形の3分の1になるのは何秒後ですか」といった、図形が全体の何分のいくつかを求める問題では、底辺の長さに着目する力が求められます。
　例えば三角形であれば、面積の公式は「底辺×高さ÷2」となりますので、高さを一定とすれば底辺の長さが半分になれば、面積も半分に、5分の1になれば面積も5分の1になります。この考え方は「比」を習った後の5年の後期以降になれば面積比の単元で演習をしますが、その基本につながる考え方です。自分で三角形をかいて、底辺の長さを5分の1になる線を引いてみると、視覚的にも面積が5分の1になることは理解しやすいでしょう。
　問題は、この底辺が必ずしも水平な位置にはないことです。下の図のように直角三角形の斜辺に点が移動した際の面積を求める場合には、視点をうまく切り替える必要があります。慣れないうちは、自分で三角形を底辺が水平になるように書きかえてみてもよいでしょう。　慣れてくればそのままの形で底辺の長さを正しく求めることができるようになります。
　さらに、最後の時間を答える際にも十分な注意が必要です。無事に底辺の長さを求められても、ほとんどの問題が「点が動き始めてからの時間」を求めさせますので、点が動いた長さをすべて加えることを忘れないようにしましょう。

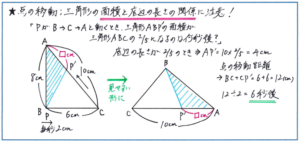
　このタイプの問題は、底辺の長さと面積の関係をしっかり理解できていれば今回のマンスリーの中でも得点源にできるものです。それだけに、長さを足し忘れるなどの細かなミスを起こさないように、最後の最後まで集中を保って解答を作るように気をつけましょう。

【第2位　旅人算：2人と1人が出会う旅人算は線分図で内容を整理しましょう！】

　今回のマンスリーでは、速さの単元から様々なタイプの問題が出されます。単純に2人が同時に出発して向かい合って出会うといった基本パターンよりも、一歩難度が増した複雑な問題への対応力が求められることが多くなります。ここが速さの踏ん張りどころです。しっかり理解を固めておきましょう。
　特に2人と1人が向かい合って同時に出発するタイプの旅人算はテストで出されることが多い問題のひとつです。内容を正確に整理できれば、解答の方針はとても立てやすくなります。そのために大きな役割を担うのが線分図です。旅人算で線分図が必要になることは塾でも何度も言われていると思われますが、特にこの2人と1人の旅人算では線分図の効果がより大きくなります。
　線分図は下のように、線分が2段か3段になります。ここでは線分どうしの間隔を近づけ過ぎないように注意しましょう。そして大事なのは、「同じ時間に3人はどこにいるか」を確実にとらえることにあります。そこで、同じ時間を表す記号を●や△などで使い分けるようにしてみるとよいでしょう。手間がかかるようですが、記号を使い分けることで、この問題のポイントである「速さの和から速さの差への切り替え」がスムーズに理解できるようになります。こうして線分図で動きや距離の変化さえ把握できれば、計算自体は複雑にはならないケースが多いです。そこが解答の方針の立てやすさにもつながるのです。

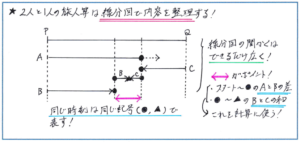
　線分図はかき慣れていれば抜群の効果を発揮しますが、慣れないうちは時間がどうしてもかかってしまいます。テストで速く正確にかけるように、普段から線分図をかくことを意識して旅人算の演習を進めておきましょう。

【第1位　速さとグラフ：グラフの形状と速さの関係は正確につかめていますか？】

　今回のマンスリーではグラフを用いた問題の多くが範囲に含まれますが、その中でも速さとグラフの問題には注意が必要です。実際の入試でも頻出の問題ですが、5年のこの時期はまだ速さの演習を始めて長く時間が経っていない段階ですので、速さの基本をしっかり踏まえたうえで、それをグラフとの関係から解かなければなりませんので、どうしても難度が上がって見えます。それでもグラフの見方さえしっかりおさえられていれば、正解に至るチャンスは十分にあり、それによりテスト全体の得点を大きくアップさせることにつながります。
ポイントとなるのはグラフの形と速さの関係です。そう聞くと難しそうですが、おさえるべきは「速さの大きさとグラフの傾きの関係」です。
　まず、グラフの形が水平になった時は、動きがない（止まっている）という点は理解しやすいでしょう。距離（グラフのたて）が変化せずに、時間（グラフの横）のみが増えて行きますので、グラフは横にまっすぐ（水平に）伸びる形になります。
　あとは速さが大きい（速い）時と速さが小さい（遅い）時のグラフの傾きですが、速さが大きければ同じ距離（たての長さ）を、より短い時間で（横の長さが短く）進むので、グラフの傾きは急に、逆に速さが小さくなれば、グラフの傾きはなだらかになります。この速さと傾きの関係がつかめれば、難度が上がった問題にも十分に対応できるようになります。

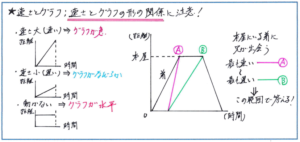
　グラフの傾きと速さの関係がおさえられれば、例えば「弟が本屋にいる間に兄が弟に会うためには、兄の速さは毎分何m以上、何m以下にすれはよいですか」といった、受験生にとって取り組みづらい「答えに幅がある問題」にも対応できるようになります。
　今回のマンスリーの対策を通して、速さとグラフの問題の基本をしっかりつかんでおきましょう。ここで基本が固まっていれば、これからの速さの問題への取り組みを一歩進んだステージで進めることができるようになります。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。