メールマガジン宝箱 Mail magazine

　今回の組分けテストは、「売買損益」「食塩水と比」さらに「変化とグラフ」といったバラエティに富んだ内容がテスト範囲となりますが、共通するポイントは、面積図や断面図をかいて問題を整理→比を利用する、の流れで解き進めることです。図の効果的なかき方をマスターして、クラスアップを実現したいところです。そこで第3回組分けテストの対策ポイントを第5位から第1位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！
　さらに、このランキングを実践的に身につけられるように予想問題を作っていますので、予想問題も併せてご活用ください！ショートバージョンは、こちらから無料でダウンロード頂けます！

【第5位　規則性：三角数の問題で「平方数」に着目できていますか？】

　規則性の問題の中で、数が横並びになる数列タイプの問題ではなく、数が表に書き込まれた数表タイプの問題や、三角形のかたちに並んだ三角数タイプの問題では、数の配置の規則を見つけ出すのに、より注意力を高める必要があります。一見すると規則性が見つけづらい印象がありますが、手がかりさえつかめれば、決して難しい内容ではありません。手がかりとして特に有効なのが「平方数（同じ数のかけ合わせた数）」です。この平方数が、三角数や数表のタイプでは列や段の端に置かれることが多くあります。列や段を表す数字と平方数の関係を正確につかめれば、どの数がどの位置に配置されているのかを、時間をかけずに、かつ正確に見つけ出すことができるようになります。
　平方数を使った問題をより速く解き進めるためにも、1から16くらいまでの平方数がしっかり暗記できているか、テスト前に確認しておきましょう。もちろん平方数について、おおよそどれくらいの大きさの数の平方になっているのか推測しても正解には十分に行き着けます。そうした推測をする力も受験算数ではとても重要な要素ですので、作業としては大事なものではありますが、制限時間のあるテスト、しかも今回の組分けではこの後に説明するような割合の重要単元や相似、グラフの活用といった、解答に時間のかかる問題がテスト範囲に含まれますので、速く解ける問題では、少しでも解答の時間を短縮しておきたいところです。

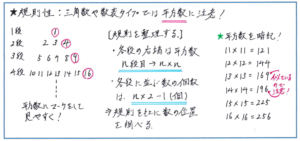
　規則性の問題では、問題への書き込みも積極的に行うようにしましょう。数や印などを書き込むことで、まとめ切れなかった内容を整理できるようになります。特に規則性が苦手なお子さんは頭の中だけで問題を処理しようとせずに、手を動かして書き込みを行い、問題内容を正確に整理するように意識しましょう。ほんのひと手間で得点のチャンスが大きく広がります。

【第4位　売買損益：仕入れ値の表し方、細かな計算ミスの防止を徹底しましょう！】

　売買損益の問題では、まずは言葉の意味を正確に理解しておきましょう。「仕入れ値（原価）」「定価」「売値」「利益」の関係を正確につかむことが、解答を進めるうえでの大前提になります。売買損益の問題は「仕入れ値の4割の利益を見込んで定価をつけましたが、売れなかったので定価の2割引きで売ったところ240円の利益がありました。この品物の仕入れ値は何円ですか。」といったかたちのように、文章の構成がある程度パターン化されています。文章を正確に式にできれば、正解に至る可能性が大きくなります。式を立てる際に仕入れ値をマル1にするかマル100にするかは、より計算が進めやすいと感じられる方で構わないでしょう。仕入れ値をマル1にすれば、複雑な小数計算が必要になりますが、最終的な計算結果として出たマル1をそのまま答えにできるケースが多くなります。マル100におくことで小数計算は少なくなりますが、最後にマル100を求めるにあたって計算（100で割るのみですが）を忘れないようにしなくてはならなくなります。
　仕入れ値をどのようにおいても、計算自体は複雑にはなります。上の例で言えば、1.4×0.8＝1.12（または140×0.8＝112）のように、スッキリとした数にならないケースが売買損益の問題では多く起こり得ます。細かな計算はできるだけ筆算で確実に進めるようにしましょう。

　そして最後に何を求めるか、仕入れ値なのか定価なのかを間違わないように、問題文に線を引くなどして、ミスを防ぐ対策をしっかりとしておきましょう。計算にしても最後に求める内容にしても、自分がどのようなミスをしてしまう傾向にあるのか、週テストや普段の演習を通して確認しておくとよいでしょう。

【第3位　相似な図形：ピラミッド型か砂時計型か、確実な判断ができていますか？】

　実際の入試でも平面図形の最頻出である「相似」ですが、問題で与えられた図形の中から相似の関係を見つけ出す際には、まずは相似の典型的なパターンである「ピラミッド型」か「砂時計型」か探すことを基本的な流れとしましょう。問題によってはそのどちらも使うケースがあります。例えば下の図の平行四辺形ABCDの中に2本の線BDとEFが入った形について、EG：GFを求める問題。すぐに目につくのは三角形EDGと三角形FBGの砂時計型の相似の関係で、しかもEG、GFは両三角形に含まれているので、この砂時計型の三角形の相似比が分かれば、それを答えにできます。そこで相似比を求めたいところですが、ここで三角形EDGと三角形FBGだけを見ていても、長さがひとつも与えられていないので、解答の方針が立たなくなります。
　そこで必要なのが「視点の切り替え」です。与えられた面積である48平方センチと60平方センチを図にかき込んでみると、DCとEFが平行であることから、三角形BCDと三角形BFGのピラミッド型の相似を使えることがわかります。
　あとは三角形BCDと三角形BFGの面積比が(48＋60)：48＝108：48＝9：4となることから相似比が3：2とわかります。四角形EFCDも平行四辺形なので、DEの長さも比の2とわかったところで、砂時計型の三角形EDGと三角形FBGに戻ります。
BF：CF＝2：1からBF：DE＝2：1より、EG：GF＝1：2と求められます。

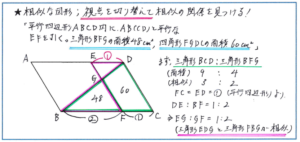
　これからの組分けテストや合不合判定テストでは、今回のような相似の関係を見つけるための視点の切り替えを求めるケースが断然増えてきます。普段の演習から図形を様々な視点で見る練習を重ねておきましょう。

【第2位　食塩水と比：複雑な混ぜ合わせの問題ではやりとりの図をフル活用しましょう！】

　食塩水の濃度の問題では、いくつかの種類の食塩水の一部をやりとりして濃度を変化させるタイプの問題が出される可能性が高くあります。やりとりの様子が具体的に把握できれば、あとは面積図や天びん図を利用すれば解答に至るまでの道筋がはっきりと見えてきます。ポイントは食塩水をやりとりした際に、濃度や食塩水の量などがどのように変化するのかを、視覚的にもわかりやすく把握することです。ビーカー図を使う方法もありますが、下のような簡単な長方形の中に、濃度・食塩の量・食塩水の量を書き込めるような図を利用すると、やりとりのイメージがつかみやすくなります。特に変わった量、変わらない量が何かを流れの中で見て取ることができる点にメリットがあります。
　もちろんビーカーの図でも同様のかたちにできますが、濃度などを書き込む場所がはっきりとルール化できますので、より速く作業を進めることができます。気をつけるのは、長方形の間隔を狭くしないようにかくことです。食塩水の移動や水の注入は矢印で表し、そこに数値を書き入れますので、ある程度スペースに余裕を持たせた方が書きやすくなります。やりとりが行われた各段階では面積図や天びん図をフル活用して、正確に数値を導き出しましょう

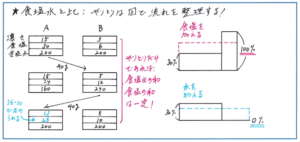
　また、混ぜ合わせの際に、食塩のみの場合は100%の食塩水、水のみの場合は0%の食塩水とすれば、水を加えた、食塩を加えたといった作業も面積図で処理することができます。いつでも面積図を使う必要はありませんが、内容を整理するための強力な武器となる面積図のかき方をテスト前にしっかり確かめておくとよいでしょう。

【第1位　水深の変化とグラフ：水そうの形とグラフの関係をわかりやすくするための断面図の利用はできていますか？】

　変化とグラフの中でも、水深の変化とグラフの問題は、変化の状況がつかみづらいこともあり、問題の難度が一気に挙がるケースがあります。もとより水そうの中で水が増えたり減ったりする様子は立体図形ならではの見方が求められ、平面図形の上を点が移動するといったタイプの問題よりも、変化のイメージがつかみづらいところがあります。問題で与えられた水そうの図にいかに正確にかき込みをしても、それでイメージがつかみやすくなるとは言い切れません。
　ここでポイントになるのは断面図の活用です。水深の変化の問題で断面図を使うケースはこれまでもありましたが、グラフと関連づけた問題では、断面図が発揮する効果がより一層高まります。
　図のような水そうに仕切りが入った問題で、断面図をかいてみましょう。わかっていない仕切りの高さはおおよそで構いません。ポイントは、断面図で分かれた3つの部分はどこも奥行きが同じですので、体積の比が断面図の面積の比と同じになります。さらに大事なのは、水そうには一定の割合で水が入りますので、「水を注ぐ時間の比＝体積の比＝断面図の面積の比」となるのです。この関係さえつかんでおけば、グラフから求められる時間を、そのまま断面図に書き込むことで、面積の比がすぐに把握できます。後は比を使うことで求める長さを計算で出せるようになるのです。

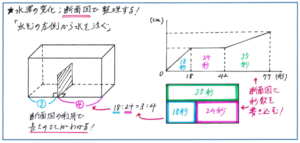
　断面図をかくのは手間ではありますが、イメージしづらい立体図形の問題を簡単に整理できる解法ですので、ぜひ試してみてください。難問で正解を勝ち取る力を一気に高めることができます。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。