メールマガジン宝箱 Mail magazine

　今回のマンスリーテストは、これまで演習してきたすべての単元が範囲となる実力テストです。苦手としている単元を復習するとともに、得点できるかどうかで偏差値が大きく変わってしまうような「差がつく問題」を確実に正解できるように、見直しを進めておきたいところです。この時期にそうした問題の対応力を強化することは、そのまま後期の志望校対策につながります。そこで8月度マンスリーテストの対策ポイントを第5位から第1位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

【第5位　数の性質：割り算に関する3つのパターンをすぐに思い浮かべられていますか？】

　数の性質の中で、「○で割ると…、△で割ると…」といった2つの割り算に関する問題に対する際には、「あまり共通型」、「不足共通型」、そのどちらでもない「バラバラ型」の3つのうち、どのパターンにあてはまるのかをすぐに思い浮かべられるようにしておく必要があります。
　「あまり共通型」とは、例えば「6で割っても8で割っても2あまる数」といったパターンで、「不足共通型」は「5で割って4あまり7で割って6あまる数」といった、どちらの数でも割り切れるためには1足りない点が共通しているパターン、そして「6で割って2あまり、5で割って4あまる数」のような、あまりも不足も共通していないパターンが「バラバラ型」となります。
　この3つのパターンのうちどれを利用するかを、問題を見てすぐに思い浮かべられるようにしておけば、問題を解くスピードが格段にアップします。3つのパターンのうち、「あまり共通型」と「不足共通型」については最小公倍数を使えば計算で簡単に解き進められます。

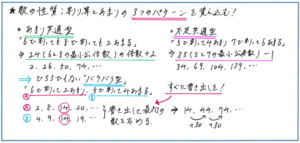
　ポイントになるのは「バラバラ型」で、最初に共通する数が出てくるまでは、それぞれに当てはまる数を等差数列のように書き出して行く必要があります。ここで書き出しに戸惑ってしまうと時間のロスになりますので、3つのパターンの見分け方とそれぞれの解き方を徹底的に頭の中に刷り込んでおきましょう。

【第4位　平面図形：相似を利用するための補助線を引くことができていますか？】

　6年生の夏休み終わりのマンスリーにもなると、単純な相似の関係を使った問題は数が少なくなり、補助線を引いて自分で相似の関係を見出して行くパターンが断然多くなります。的確な補助線を瞬時に引くことができれば、自分の解きやすいかたちにスムーズに持ち込めるようになります。
　特に下の台形のようなシンプルな図形では補助線の引き方ひとつで、かかる時間と正確さに大きな差が生まれます。相似を利用しやすい三角形を作り出すことが大事ですので、左の図のように三角形が2つになるような補助線を引く方法もあります。もちろんこのかたちでも正解には行き着くのですが、相似を使った計算を2回しなければならなくなります。しかも三角形の上下の向きが逆になりますので、それぞれに応じた比を正確に使い分ける必要も出てきます。
　そこで右の図のように平行四辺形と三角形に分けるように補助線を引けば、平行四辺形の性質から分けられた線分の一方の長さがすぐにわかり、相似を使った計算は1回で済むのです。

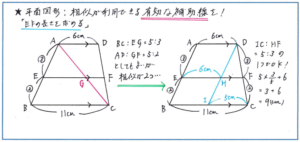
　こうしたタイプの問題はテストでは図形の小問集合や、大問の(1)などで出されることが多く、何としても得点しておきたい問題になります。図形を見てすぐに補助線を引けるように、同タイプの問題をしっかり見直しておきましょう。

【第3位　速さの問題：峠（坂道）の問題は消去算で攻略しましょう！】

　速さの問題の中で、行きはある地点まで坂道を上り、そこから坂道を下り、帰りは同じ道を上り、下るという進み方をする問題があります。複数の人物が動く状況を解くといった複雑さはないものの、道のり、速さが2種類あることで、合計4種類の状況が生まれるため、スムーズに正解に行き着くためには問題内容を正確に整理する必要があります。そこで下のように、それぞれの状況を表でまとめてみると、行きにかかった合計時間と帰りにかかった合計時間がわかっていることから、それを使った2つの式を導き出すことができます。
　あとは消去算の考え方で各状況でかかった時間を求められますので、解答の道筋が一気に見えてきます。この消去算を使うという方針がはっきりしていれば、いくつかの状況が組み合わさった問題でも、焦らずにひとつひとつの状況を整理して行けばよいと思えるようになります。

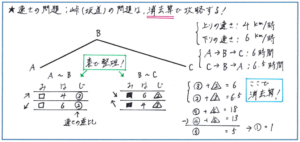
　こうした消去算を利用した解き方は、速さだけでなく仕事算や相当算、そして図形の問題でも多く使われることがあります。式さえ立てられれば消去算が使える、というのは安心材料にもなりますので、消去算が使える段階までの、問題内容を整理→式を立てる、という流れをしっかり身につけておきましょう。

【第2位　平面図形：図形の中の直線を分ける比の求め方は身についていますか？】

　今回のマンスリー、後期のオープンテスト、そしてもちろん実際の入試でも、平面図形の中に複数の直線が書き込まれたかたちを題材とする問題は頻出です。その中でも複数の相似の関係を使って直線の長さの比を求める、下の図のようなパターンは様々なタイプの問題で使うケースが出てきますので、解き方を確実に覚え込んでおきましょう
　ポイントとなるのは、2つの相似の関係を的確に見つけ出すことです。このタイプの問題では相似の関係にある図形の向きが変わってきますので、どのような向きに図形がつながっていても相似の関係を見つけられるように、特に砂時計型の相似の基本形は頭の中でイメージを固めておきましょう。
　そして相似の関係が見つかった時点で、図に書き込みをしておくことが必須です。最小公倍数が簡単に見つけられるからといって、頭の中だけで処理しようとすると、細かな値のところでミスが発生し、失点につながります。時間がないからといって手を使うことを省かずに、丁寧に書き込みをしておきましょう。書き込みさえしておけば、そこからの計算は一気にスピードアップさせることができます。

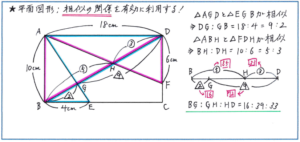
　これから受けるテスト、そして過去問で出題される平面図形は複雑さを増してきます。そうした問題に対応するには的確な「図形の切り取り」が必要になります。複雑な図形の中から有効に活用できる相似の関係、面積比の関係を切り取り、そこから必要な長さの比などを順に求めて行ければ、難問にも正確に対応できるようになります。まずは相似の基本形をしっかり確認しておくようにしましょう。

【第1位　立体図形：立体の切断の基本性質を使いこなせていますか？】

　立体図形の中でも難度が高い「切断」は、以前は出題が難関校に限定される傾向がありましたが、最近の入試では学校の偏差値レベルに関わらず広く多くの学校で出題されるようになっています。この切断の問題での得点がテスト全体の点数を底上げするポイントになりますので、切断の際に立体の辺や面がどのような関係にあるかといった、切断の基本性質は確実におさえておきましょう。
　特に大事なのが、「向かい合う平面上にある切断面の線は平行になる」という点です。立体図形の難しさは図形のかたちや長さの関係などがイメージしづらい点にあります。この線どうしの平行関係も立体図形のままではイメージしづらく、正しく位置関係をとらえづらくなります。そこで、立体を上や横から見た「平面」で平行な関係を整理すると、一気にわかりやすくなります。
　この平行の関係さえつかめれば、線の長さなどがどんどん見えてきて、求めたい値に近づくことができます。切断面自体は五角形や六角形など複雑な図形になりますが、求める長さが含まれる図形は三角形などシンプルなかたちになることが多いです。

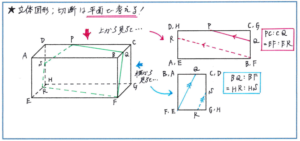
　立体図形では相似の関係にある平面図形の位置が離れてしまうことで、どのように解き進めてよいのか、迷ってしまうことが起こりがちです。そうした事態にならないように、平面図形に当てはめて解く方法をしっかり身につけておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。