メールマガジン宝箱 Mail magazine

　今回のマンスリーテストでは、何といっても中学受験算数の最重要単元「比と割合」でどれだけ得点できるかが最大のポイントになります。夏期講習で学習した「比と割合」の考え方は、文章題、図形問題問わずあらゆる単元で利用することになります。まずは今回のマンスリー対策を通して、比と割合の基本的な考え方、図形問題での比の使い方、売買損益、食塩水の問題といった文章題の解き方を確実におさえておきたいところです。そこで8月度マンスリーテストの対策ポイントを「比と割合」に絞って、第5位から第1位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

【第5位　比と割合（基本）：問題文から比と割合の関係を正確に表すことができていますか？】

　今回の夏期講習で演習した「比と割合」についてはマンスリーテストでも多くの問題が出される可能性がありますので、少し時間をかけてでも徹底的に基本固めをしておく必要があります。
 　その基本ですが、まずは問題文の内容を正確に比、割合で表すことが必須です。例えば「62個のおはじきをA、B、Cの3人でわける際に、それぞれが受け取った個数は、AがBの1.5倍、BがCの3/8（8分の3）倍のとき、Bが受け取ったおはじきは何個ですか」といった問題。A、B、Cが受け取るおはじきの個数を比で表して、62個をその比で配分する、という方針になります。
　そこで「AがBの1.5倍、BがCの3/8倍」の内容をそれぞれ式にして、A：B、B：Cの比を求めるところからスタートします。まず、A＝B×1.5、B＝C×3/8という式が立てられますが、この式がたてられなかった場合は、割合の基本範囲を徹底的に復習してください。この段階が習得できていないと、この単元での得点は難しくなります。
　次に1.5＝3/2なので、A＝B×3/2の式からA：Bの比を考えます。ここでは3/2にかけて答えが整数になる最も簡単な数である、分母の2をBとして、2×3/2＝3よりA＝3、よってA：B＝3：2となります。このBを2として計算する流れを身につけておけば、分数を含む式から比をスムーズに求められるようになります。同様にして、B＝C×3/8からB：C＝3：8となりますので、連比の考え方で、A：B：C＝9：6：16と求められます。
　あとは62を9：6：16の比で分けたうちの6を求めますので、62×6/(9＋6＋16)＝62×6/31＝12より、Bが受け取るおはじきは12個となります。

　これからの算数の演習では比と割合の考え方を使わないケースはほとんどないといっても過言ではありません。この単元で習うひとつひとつの考え方、解き方は受験算数の大事な基盤となりますので、まずは基本でもれがないように、しっかり見直しをしておきましょう。

【第4位　立体図形と比：3.14を使わずに比で解き進める方法を使いこなせていますか？】

　立体図形には計算が複雑になってしまう問題が多くありますが、それらの問題でも比を使うことで解き方が断然楽になります。
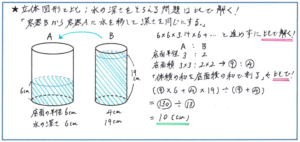
　ここでは、2つの円柱の容器に入った水をやりとりして、水の深さを等しくするような問題を例に考えてみましょう。下の図のような「底面が半径6cmの円である円柱の容器Aと、底面が半径4cmの円である円柱の容器Bがあり、容器Aには深さ6cm、容器Bには深さ19cmまで水が入っています。容器Bから容器Aにこぼれないように水を移して、2つの容器の水の深さが同じになるようにした時に、水の深さは何cmになりますか」といった問題で、比を使った解き方を考えてみます。
　まずこうした水の深さを同じにする問題では「水の体積の和を、底面積の和で割る」という方針になることはしっかりおさえておいてください。そこでいざ計算なのですが、底面の円の面積を求める際に3.14が入り、さらに容器Bの水の深さが19cmという大きな値ですので、計算が複雑になると予想されます。
　そこで、比を使う解き方で進めてみましょう。容器Aと容器Bの底面の半径の長さの比は、6：4＝3：2ですので、底面積の比は3×3：2×2＝9：4となります。ここで容器Aの底面積をマル9、容器Bの底面積をマル4と置いて、そのまま体積の計算を進めます。容器Aの水の体積は、マル9×6＝マル54、容器Bの水の体積は、マル4×19＝マル76となります。
　最後に、先ほど触れました「水の体積の和を、底面積の和で割る」の考え方から、水の深さを求めて行きます。水の体積の和が、マル54＋マル76＝マル130で、底面積の和がマル9＋マル4＝マル13ですので、マル130÷マル13＝10より、水の深さは10cmと求められます。

　比は慣れるまでは扱いづらく感じるかもしれませんが、使いこなせるようになると、単元を問わす利用できるうえに、計算が圧倒的に楽になるという大きなメリットがあります。すぐに計算で解くのではなく、まず比が使えないかどうか、考えてみるようにしましょう。ただし、テストでは時間が限られますので、比の使い方が思い浮かばなかった場合は、そのまま計算で進めるようにしてください。

【第3位　売買損益：割引き・割増しが2回以上ある時の式の立て方に要注意です！】

　比と割合の文章題の中で特に注意しておきたいのが、「売買損益」と「食塩水の濃度」の問題です。それぞれの問題に出てくる言葉の意味を確実に把握して、正確な式を立てることが今回のマンスリーの偏差値アップにつながります。
　売買損益では、価格の設定が2段階になる問題に注意が必要です。例えば、「原価の3割の利益を見込んで定価をつけましたが、売れなかったので定価の20%引きを売値とした場合、何%の利益が出ますか」といった問題であれば、原価（仕入れ値）を1として、定価が1.3でそこから20%引き＝80%の価格が売値なので、「1.3×0.8＝1.04」より利益は「1.04－1＝0.04」より4%の利益と求められます。このかけ算を連ねる式は基本ですので、式が立てられない場合は急ぎデイリーサピックスで復習をしてください。
　これが「原価の3割増しで定価をつけましたが、売れなかったので390円値引きして売ったところ、原価の17%の利益が出ました。原価はいくらですか」といった問題になった場合にも正確に対応できていますでしょうか。売買損益の問題の難しさのひとつは、言葉の使い方が少し変わっただけで解きづらさが一気に増してしまうことにあります。言葉の基本的な意味に立ち返って、やはり原価を1として式を考えると、定価は1.3で売値は原価に利益の17%を加えた1.17となります。この1.3と1.17の差が値引き分の390円に当たりますので、原価をマル1とすると、マル1.3－マル1.17＝マル0.13が390円となることから、マル1＝390÷0.13＝3000より、求める原価は3000円となります。

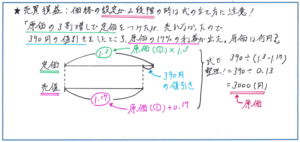
　売買損益の問題では価格の変化を正確に把握するために、言葉の意味を正しくおさえておくことが必須ですが、理解をより確実にするためには、線分図で整理することも有効です。慣れれば線分図なしでも解き進められますが、言葉の意味が自分の中にしっかり浸透するまでは、線分図で整理するという作業が効果的です。

【第2位　平面図形：底辺の長さの比を使う面積比の問題で補助線を有効活用できていますか？】

　平面図形でも、比を使って解く問題が多く出される可能性が高くありますが、まだ「相似」を習っていない現段階では、「面積比」の問題への対応力が問われることになります。
　特に三角形の面積比で、「高さが共通の三角形の面積比は底辺の長さの比と同じになる」という性質を使った問題では、補助線を使って解き進める必要があります。例えば下の図のような小さい三角形をいくつかの三角形で囲んで大きな三角形となったかたちの問題では、補助線をどれだけ速く引けるかが、時間を短縮して正解に行き着くためのポイントになります。
　下の図で、点線で表した補助線を引くことができれば、となり合う三角形の面積比を底辺の長さの比から求めることができ、それをたして行けば小さい三角形と大きな三角形の面積比も複雑な計算なしに導くことができます。

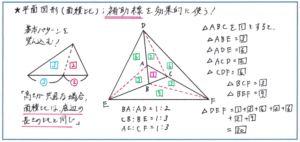
　正解に直結するような補助線を引けるようになるためには、上の左に示したような面積比と底辺の長さの比の関係を端的に表したシンプルな図をしっかり頭の中に刷り込んでおくとよいでしょう。その図をもとに問題の図を見ると、自分が引くべき補助線のイメージが鮮明に浮かんできます。図形の問題はイメージが重要です。問題を見て起点となるイメージを抱けるように、典型的な図形のパターンを何度も見ておくようにしましょう。

【第1位　食塩水の濃度：混ぜ合わせの問題で面積図を利用できていますか？】

　比と割合の中でも食塩水の濃度の問題は、これからのテストでも頻繁に出題される重要単元です。食塩水を混ぜ合わせる回数が複数になるなど、その複雑さは増して行きますが、まずは今回のマンスリー対策を通して、基本的な混ぜ合わせの問題を正確に解けるように、特に面積図をスムーズにかけるように練習を重ねておきましょう。　
　混ぜ合わせの問題で、例えば「8%の食塩水200gと12%の食塩水300gを混ぜると、何%の食塩水ができますか」といった問題であれば、面積図を使わなくても2つの食塩水に含まれる食塩の量がわかり、食塩水の合計も200＋300＝500（g）とすぐに出せることから、面積図を使わなくとも計算で濃度を求めることができます。
　ただ、次のような問題ではどうでしょうか。「12%の食塩水（ア）gと、4.5%の食塩水（イ）gを混ぜると、10.5%の食塩水が500gできます。（ア）と（イ）にあてはまる数を答えなさい」といった問題になると、2つの食塩水について、濃度、食塩水の量、食塩の量のうちわかっているのが濃度のみですので、計算で解き進めることが極めて困難になります。そこで面積図を利用すると、瞬く間に正解まで行き着くことができます。

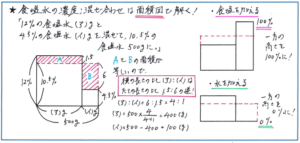
　面積図の基本的なかき方が理解できていない場合には急ぎ優先して復習を進めてください。先にご紹介した食塩の量が計算で出せるような問題を使って、面積図をかく練習を重ねてもよいでしょう。問題の内容にかかわらず食塩水の濃度の問題に対応できるだけでなく、比を使う問題であればどの単元にでも対応できるのが面積図です。今回の対策を通して速く正確に面積図をかけるようにしておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。