メールマガジン宝箱 Mail magazine

　6年生最後の組分けテストです。これまで習ったすべての単元が範囲となる実力テストですので、苦手意識の強い単元の問題はもちろん、これまでのテストであと一歩で正解に届かなかった問題をしっかり見直しておく必要があります。そして解法の工夫が覚えられているか、比を利用する問題で解答方針が立てられているか、図形に的確な補助線が引けているか、といった高得点に直結するポイントが身についているかをチェックしておきたいところです。そこで第4回組分けテストの対策ポイントを第5位から第1位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

【第5位　和と差に関する問題：問題内容から解答方針を見つけるための線分図がかけていますか？】

　和と差に関する問題の中には、一見複雑そうでも線分図で内容を整理すれば、解答方針がハッキリと見えてくるタイプの出題があります。早速例題を挙げてみましょう。
　「おはじきを男子と女子に配ります。男子に5個ずつ、女子に3個ずつ配ると18個あまり、男子に8個ずつ、女子に6個ずつ配ると12個足りません。男子の人数が女子よりも2人多いとすると、おはじきは全部で何個ありますか」といった過不足算の問題。男子と女子の人数の差がわかっていますので、男子の人数を、女子＋2人として、「すべてを女子」に置き換えて解く方法があります。もちろんこの解法も覚えておきたいですが、おはじきの個数を調整するのが難しく、ミスが起こってしまいがちです。
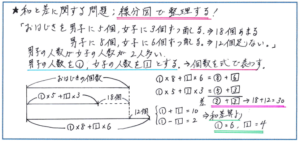
　そこで、下のような線分図で整理をしてみます。ポイントは男子の人数をマル1人、女子の人数をシカク1人として、線分図から、マル5＋シカク3で表される個数と、マル8＋シカク6で表される個数の差が、18＋12＝30（個）になる、という関係をつかむことです。
　ここからは数の成り立ちをよく見て、マル8＋マル6の式からマル5＋シカク3の式を引くと、「マル3＋シカク3」が残ることを見逃さない注意しましょう。そこさえ把握できれば、あとはマル3＋シカク3が30個にあたることから、マル1＋シカク1＝10となり、マル1－シカク1＝2（人数差が2人）となるので、和差算の考え方で男子6人、女子4人と人数が算出でき、おはじきの個数も5×6＋3×4＋18＝60（個）と求められます。

　過不足算に限らず和と差に関する問題は、思わぬところで数を取り違えてしまうことがあります（あまりと不足の個数など）。線分図などで視覚的に内容を整理できれば、そうしたミスを大きく減らすことができます。ぜひ図を使った解法を試してみてください。

【第4位　平面図形：覚えておくべき解き方の工夫を確認しておきましょう！】

　平面図形・立体図形では、覚えておくとおかないとで、解答にかかる時間と正確さに大きな差が生まれる「解き方の工夫」があります。その代表例は、円すいの側面積です。円すいの側面は展開図にすると、おうぎ形になりますが、その面積を求める「母線×底面の半径×円周率」の式は、6年生の皆さんはこれまでに多くの問題で利用してきたでしょう。
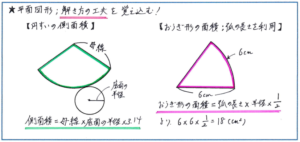
　それ以外に覚えておきたいのが、弧の長さがわかっているおうぎ形の面積を求める「弧の長さ×おうぎ形の半径×1/2」の式です。
　下の右の図のような、半径6cm、弧の長さが6cmのおうぎ形の面積を求める場合、先ほどの工夫した解き方が頭の中に入っていなければ、中心角（中心角/360度の値）を求めることから始める流れになります。中心角を□度とすると、「6×2×3.14×□/360＝6」という式が立てられ、3.14×□/360＝6÷(6×2)＝1/2と求められます。面積を求める式を立てると、6×6×3.14×□/360＝6×6×1/2となり、先に挙げた式「弧の長さ（6cm）×底面の半径（6cm）×1/2」が成り立つことがわかります。

　式で地道に進めることも大事ですが、上記のような分数を含む長い式ではミスが起こりやすくなってしまいます。ただでさえ時間配分が重要な組分けテストですので、可能な限り時間を短縮できる問題を増やしておきたいところです。そのためにも、今回ご紹介したような解き方の工夫をテストで使いこなせるように、暗記を確認しておきましょう。

【第3位　集合：問題内容を整理するための表を使えていますか？】

　集合の問題で、与えられた条件を正しく整理して解き進める際には、条件を自分にとってわかりやすく、できるだけ短時間でまとめることがポイントとなります。集合ではベン図や線分図などを使って解くことができますが、有効なツールのひとつに「表」があります。
　例えば次のような問題。「30人のクラスのうち、女子の人数は14人です。また、1月から6月生まれの生徒が13人います。女子で7月から12月生まれの生徒が7人のとき、男子で1月から6月生まれの生徒は何人ですか」といったタイプの問題で、表を使った解法を確認してみましょう。

　上の表のように、男子・女子の人数、1月から6月生まれ、7月から12月生まれの人数、そして合計人数から成る表を作り、問題文からわかる数値をどんどん枠内に埋めて行きます。
　この問題の場合、男子、女子それぞれの合計人数、さらに1月から6月生まれ、7月から12月生まれの合計人数がわかっていますので、そこから4つの枠の人数のうちどれか1つがわかれば、後はまるでドミノ倒しのように、数が判明して行きます。
　問題文を読むと、人数を表す内容がいくつにも分かれそうで、解答がとても煩雑になってしまう印象を持ってしまいますが、いざ表にしてみると、知るべき人数は4種類、それもそれぞれが深く関係していることで、今回のように1つの要素の人数さえわかれば一気に解き進められます。集合の問題であればベン図か線分図と決めつけずに、表も使えることを念頭に置いて問題に臨むようにしましょう。

【第2位　平面図形：相似・面積比を利用する解法「つの出し」は習得できていますか？】

　今回の組分けテストでは、相似や面積比といった「比」を利用するタイプの問題が出される可能性がとても高いです。実際の入試でも「相似・面積比」は図形分野の最頻出単元であるだけに、6年最後の組分けでもこの単元から応用問題が出題される傾向にあります。
　例えば下の図のような台形を題材とした問題で、台形の内部に引かれた直線の長さを求めるといった場合、多く使われる方法は、「台形を平行四辺形と三角形に分ける補助線」を引いて、相似の利用に持ち込むパターンですが、その場合は台形の脚にあたる辺を分ける長さの比（図であれば、AP：BPまたはDQ：CQ）が与えられなくてはなりません。この問題のようにそれがわからない場合は、どのように対応すればよいでしょうか。

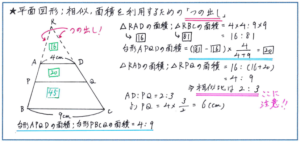
　そこで有効なのが、図のように台形の脚の部分の辺を上方に伸ばして、その交点を頂点とする三角形の相似で考える、「つの出し」の解法です。三角形RADの面積：三角形RBCの面積＝16：81になることから、台形APQDの面積が比の20にあたり、三角形RADの面積：三角形APQの面積＝16：36＝4：9になります。面積比から相似比を算出すると、三角形RADと三角形APQの相似比が2：3になるので、PQの長さは、4×3/2＝6（cm）と求められるのです。
　この「つの出し」の解法は平面図形だけでなく、立体図形の切断などでも多用されますので、解き方の流れをしっかり確認しておきましょう。

【第1位　速さとグラフ：速さ、道のり、時間の比の関係をグラフから読み取れていますか？】

　平面図形と同じく、速さの単元からも「比」を使って解くことが求められる問題、グラフを使った問題などの難問が、今回の組分けテストで出される可能性が高くあります。ポイントになるのは、グラフの中から速さ、道のり、時間の比の関係を確実に読み取ることです。速さが同じであれば、時間の比＝道のりの比となり、時間が同じであれば、速さの比＝道のりの比に、そして道のりが同じであれば、速さの比と時間の比が逆比になる、という3つの比の関係はすでに定着していると思われます。それがグラフの中ではどのように表されるかがすぐにわかるように、比とグラフの関係は重点的に見直しておきましょう。

　上記の3つのグラフのパターンは一例ですが、読み取りのポイントとなるのは「同じ部分」がグラフでどう表されるかを把握することです。速さが同じ場合はグラフの傾きが同じになり、時間が同じ場合はグラフの横軸（時間を横軸とした場合）、道のりが同じ場合はグラフのたて軸（道のりをたて軸とした場合）が同じになります。それぞれを表すグラフのかたちをしっかり頭の中に植え付けておけば、テストでグラフを見た際にスムーズに対応することができます。グラフ問題をしっかり見直しておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。