メールマガジン宝箱 Mail magazine

　今回の5年生夏期講習マンスリーテストの最大のポイントは、何といっても中学受験算数の最重要単元「比と割合」でどれだけ得点できるかにあります。この「比と割合」の登場から、中学受験の算数は新たなステージにレベルアップすることになります。今後の算数において、文章題、図形問題に関わらず、あらゆる単元で利用することになるのが「比と割合」です。今回のマンスリー対策を通して、まずは比と割合の基本的な考え方、食塩水の濃度、売買損益とった文章題の解き方、そして図形問題での比の使い方を確実におさえておきたいところです。そこで「比と割合」を中心に、夏期講習マンスリーテストの対策ポイントを第5位から第1位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

【第1位　食塩水の濃度：問題内容に合わせて面積図をフル活用できていますか？】

　「比と割合」の単元の中でも食塩水の濃度の問題は、入試問題を含め、これからのテストで頻出度が非常に高い重要単元です。特に食塩水を混ぜ合わせる問題は、何度も混ぜ合わせを行う「やりとり」の問題のようなタイプになると複雑さが一気に増し、難度が上がってきます。そうした難問に対応するには「面積図」が不可欠ですので、まずは今回のマンスリー対策を通して、基本的な混ぜ合わせの問題で正確にスムーズに面積図がかけるように練習を重ねておきましょう。　
　例えば次のような問題を見て、すぐに面積図がかけるでしょうか。
「15%の食塩水（ア）gと、7.5%の食塩水（イ）gを混ぜると、12%の食塩水が500gできます。（ア）と（イ）にあてはまる数を答えなさい」
　このような問題では、2つの食塩水について、濃度、食塩水の量、食塩の量のうちわかっているのが濃度のみですので、計算で解くのは困難になります。そこで面積図を利用すると、複雑な計算をすることなしに正解まで行き着くことができます。

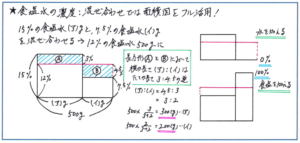
　また、図の右側にあるような、「食塩を加える」「水を加える」といったケースでも面積図を使って解くことができますので、それぞれのかき方を覚えておきましょう。
　今回のテスト範囲では、「平均算」でも面積図を使って解くことができる問題が出てきます。そして今後、速さを含め、比を使った問題ではどの単元にでも対応できるのが面積図です。今回の対策を通して正確にスムーズに面積図をかけるようにしておきましょう。

【第2位　点の移動：面積の変化を「場面分け」して把握できていますか？】

　「点の移動」の問題では、動く点によってできる図形の面積の変化が出題対象となることが多いです。時にその変化がグラフによって表されることもありますが、変化の状況をどれだけ正確に把握できるかが得点の分かれ道になります。
　その面積の変化について、頭の中だけでイメージしようとすると、思わぬ見逃しがあり、結果として時間がかかるばかりで得点にならないといった事態になりがちです。動く点が1つだけであればまだ頭の中でイメージできますが、速さの異なる2点の動きとなると、動きのイメージが一気にしづらくなります。面積の変化を正確に把握するためには、自分で図をかいて、点の位置によって「場面分け」をしてそれぞれの面積を求める必要があります。
　例えば下の図で、平行四辺形ＡＢＣＤの辺ＡＤ上を点Ｐが頂点Ａを、辺ＢＣ上を点Ｑが頂点Ｂを同時に出発して、辺上を往復する際の四角形ＡＢＱＰの面積の変化を考えるとします。点Ｐが点Ｑより速く動くとした場合、まず点Ｐが頂点Ｄに着く時点（下の図①）、次に点Ｑが頂点Ｃに着く時点（下の図②）、点Ｐが頂点Ａに着く時点（下の図③）、そして点Ｑが頂点Ｂに着く時点（下の図④）として場合分けします。

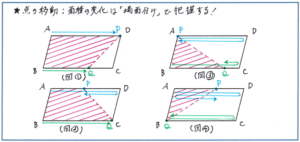
　注意すべきは、これはあくまで基本形で、例えば点Ｐと点Ｑの速さの差が大きい場合には、点Ｐが往復して点Ａに戻りつく方が、点Ｑが点Ｃに着くよりも早いケースがあります。その場合も、各点が頂点に着く時間が算出できれば、基本形を変更させて簡単に状況が把握できます。そしてこのタイプの問題の多くがグラフとの関係を含めてきます。一見より複雑になる印象がありますが、グラフによって点の速さや辺の長さといった、面積の変化を把握するうえで必要なデータが得られますので、グラフの変化する点に注目して、グラフから与えられる数値をフル活用する練習も重ねておきましょう。

【第3位　売買損益：割増し・割引きが2回以上ある時に正確に式を立てられていますか？】

　「比と割合」の文章題の中で「食塩水の濃度」と共に注意しておきたいのが、「売買損益」の問題です。まずは問題に出てくる「原価（仕入れ値）」「定価」「利益」といった言葉の意味を確実に把握して、それぞれの関係を正確に理解することが大前提となります。
　そのうえで、価格の設定が2段階またはそれ以上になる問題に注意が必要となります。例えば、「ある品物を何個か仕入れ、1個につき原価の4割の利益を見込んで定価をつけましたが、売れなかったので定価の20%引きですべて売ったところ、2400円の利益がありました。この品物の仕入れ値は何円ですか」といった問題であれば、原価（仕入れ値）を1として、定価が1.4でそこから20%引き、つまり80%の価格が売値なので、「1.4×0.8＝1.12」（この式の立て方を間違わないように！）より利益は「1.12－1＝0.12」から、仕入れ値の12%となり、2400円であることがわかります。最後は相当算の考え方で、0.12が2400円に当たることから、2400÷0.12＝20000（円）として、仕入れ値を求めることができます。
　売買損益の問題では、「利益を見込む」など、この単元ならではの言葉の使い方がありますので、まずはその意味を正確に把握して、求める値段を1とおくことからスタート、計算ではかけ算を正確に使いこなすといった流れを丁寧に、かつスピーディーに行えるように、デイリーサピックスの問題をくり返し演習しておくようにしましょう。

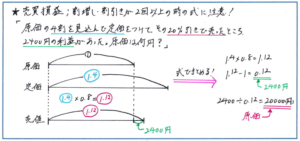
　売買損益の問題では、言葉の意味をより確実に理解するために、慣れないうちは線分図で整理することも有効です。言葉の意味が頭の中にしっかり浸透するまでは、図をかくことを心がけましょう。

【第4位　円を転がす：多角形の頂点を曲がる時の面積の合計をスムーズに求められますか？】

　「円と多角形」の中で、多角形の外側を辺にそって円が転がるタイプの問題では、円が動いたあとの図形をイメージできても、いざ面積を求める際に「円が頂点を曲がる」部分をどれだけ速く正確に導き出せるかが、その問題の得点だけでなく、テスト全体の時間配分に大きく影響を及ぼします。例えば下の図のような四角形の外側の辺にそって円が転がって一周する場合、円が動いたあとの図形の面積は、4つの長方形と4つのおうぎ形の合計になります。

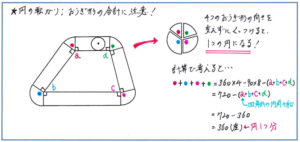
　この4つのおうぎ形の面積の合計が、円1つ分になることについて、図のようにおうぎ形を向きを変えずにくっつけて円とする考え方と、おうぎ形の中心角を計算で考える方法があります。どちらでも理解しやすい方で覚えておくと良いですが、これは多角形の外側を円が転がって1周する場合にあてはまることで、この単元からは様々な「円の転がり」が出題対象となりますので、機械的に「円1つ分」と覚えるのではなく、必ず円の動いたあとの図形を正しく把握してから考えるように注意しましょう。

【第5位　比の基本：問題文から正確に比の関係を表せていますか？】

　今回の夏期講習で演習した単元の中でも「比と割合」については、今後の算数の礎となりますので、少し時間をかけてでも優先して基本固めをしておきましょう。
　基本として、まずは問題文の内容を正確に比、割合で表せるようになることが必須です。特に機械的に比で表そうとするのではなく、比の成り立ちをしっかり踏まえたうえで考えることが重要です。例えば「えんぴつ8本とボールペン6本と消しゴム9個の値段はすべて等しいです。えんぴつ1本とボールペン1本と消しゴム1個の値段の比を答えなさい」のような、3種類の品物を対象とした場合、2種類の品物を対象とした場合の解き方よりも比の成り立ちをより強く意識する必要があります。これが「えんぴつ8本とボールペン6本の値段が等しいときの、えんぴつ1本とボールペン1本の値段の比を答えなさい」という問題であれば、「6：8＝3：4」とすぐに答えを求められますが、ここでただ「数字を逆にする」という覚え方をしてしまうと、品物が3種類になると対応できなくなってしまいます。えんぴつ8本とボールペン6本の値段を「1」とした場合、えんぴつ1本の値段が「1/8」ボールペン1本の値段が「1/6」として表せるため、「1/8：1/6＝6：8＝3：4」という流れをしっかりつかんでおけば、3種類になっても「1/8：1/6：1/9＝9/72：12/72：8/72＝9：12：8」として正解に行き着くことができます。

　今回ご紹介したタイプの問題は、テストの中盤で出される可能性が高く、正解できるがどうかがテスト全体の得点に大きく影響を及ぼす「分水嶺」となるものです。さらには今後、難度を増して行く比の問題でも高い正答率を取り続けるためには、機械的な解き方を覚えるのではなく、比の基本的な成り立ちを強く意識して解く習慣をつけておく必要があります。テスト前に、機械的な覚え方をしていないか、いま一度確認をしておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。