メールマガジン宝箱 Mail magazine

　今回の5年生11月度マンスリーテストでは、「相似」そして「面積比」という入試頻出の図形問題が範囲に含まれます。10月マンスリーでは「比と速さ」、11月マンスリーでは「比と図形」そして12月マンスリーでは倍数算など「比と文章題」と、立て続けに比を使う重要単元が出題されるこの時期は、まさに中学受験算数における「踏ん張りどころ」と言えます。ここでのテスト対策を通してじっくり足場を固めることが、今後の算数での得点力アップを実現させるために必須となります。その他にも速さの重要単元「流水算」「通過算」も範囲となる今回のマンスリーで、何としてもクラスアップを達成したいところです。そこで、「比を使って解く問題」を中心に、11月度マンスリーテストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでください！応援しています！
　さらにこちらの算数予想問題と組み合わせれば、マンスリーテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　比と図形：向きの異なる相似な図形の対応する辺が正しく求められていますか？】

　今回のマンスリーテストのメイン単元のひとつが「相似」です。夏期講習から演習してきた「比」を図形の中で利用して解くこの「相似」は、入試問題での平面図形最頻出の重要単元です。相似の問題を正確に解き進められるかどうかが、今後の算数のテスト、そして入試算数で高得点をとるための必須のポイントとなります。今回のマンスリー対策を進める中で、相似の基本をしっかり固めて行きましょう。
　まずは、相似の関係にある図形の「辺の長さの比」を正確に求めることが最初のステップとなります。基本的なピラミッド型やクロス型の形であれば、見た瞬間にどの図形とどの図形が相似かがわかりますが、気をつけなくてはならないのが「向きの異なる相似な図形」です。例えば下の図のように、辺の長さの一部が与えられていても、対応する辺を間違ってしまっては、正解に至ることはできません。こういった問題の場合、塾の授業でも指示されていると思われますが、「同じ角度に印をつける」ことで、辺の対応が見やすくなります。角度に印をつけた上で、下の右の図であれば、角度の「△→○→●」の順に、向かい合う辺の長さの比が、アの図形では、「15：a：12」、イの図形であれば「24：18：b」となり、その比が等しくなります。あとは、a＝18×15/24＝18×5/8＝11.25（cm）、b＝12×24/15＝12×8/5＝19.2（cm）と、値を求めることができます。

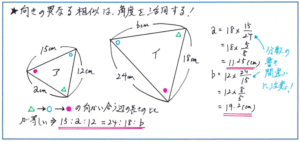
　ここでご紹介したタイプの問題は、テストの前半で出される可能性が高いので、ぜひとも得点しておきたいところです。そして、この向きの異なる相似の図形での対応する辺の関係を正確に求められる力は、後半の大問に対応する場合にも必要になります。見た目で判断しようとするとミスを起こしてしまいますので、書き込みを的確に行って、慎重にかつスピーディーに対応する辺の関係を求められるように練習しておきましょう。

【第2位　比と図形：クロス型の相似をつくるための補助線を正確にひくことができていますか？】

　相似の問題で、【第1位】でご紹介しました内容からさらにレベルアップした問題として、長方形や平行四辺形、台形の中にある相似の関係を的確につかむ力が求められる問題があります。テストの中盤以降に出てくる可能性が高く、まさに得点の分かれ道になる重要問題となります。
　特に注意しておきたいのが、与えられた線だけで相似の関係を見つけることができないケースです。例えば下の図のように台形ABCDの中に2本の直線がひかれている問題。まず辺ABと辺CDが平行ではないので、三角形ABFと三角形CEFは相似の関係にはなりません。そこで、辺ADと辺BCが平行であることから、「あと一歩でクロス型の相似になる」と考えられれば、それだけでも正解への大きなステップになります。与えられた図形で相似がなければ、自分でつくってしまえばよいのです。ADとBFをそれぞれ延長させた線の交わる点をGとすれば、三角形AGFと三角形CBFが相似となります。さらに、三角形DGEと三角形CBEも相似になります。ここでAF：CF＝1：1であれば、AGの長さは、BCと同じく25cm、GDの長さが25－18＝7（cm）より、CE：DE＝BC：GD＝25：7と、比を求めることができます。線を延ばして新しい三角形をつくる手間がかかりそうですが、相似の関係を一旦つくってしまえば、比や長さがいもづる式にわかって行きます。この流れをぜひつかんでおいてください。

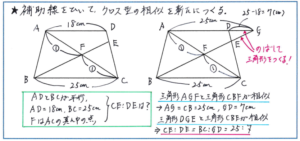
　相似の関係にある図形を自分でつくる際に注意しなくてはいけないのが、「平行線」です。上記の図形であれば辺ADと辺BCのように、平行な関係さえつかめれば、相似の図形はつくりやすいです。また、クロス型の相似の関係を図形の中に見出す意識を固めるために、相似の基本型を頭の中に刷り込んでおくようにしましょう。

【第3位　比と図形：「三角形を区切る」問題では解答の流れを確実に身につけておきましょう！】

　比と図形の問題の中で、下の図のような三角形を区切るタイプの問題は、一見複雑そうで、解き方さえしっかり固まっていれば、いたってスムーズに解き進められます。ポイントは三角形の図の中に、与えられた比を書き込んで、比の値を取り違わないようにすること。あとは、分数のかけ算を進めれば、中央の三角形が大きな三角形の何倍かをすぐに求めることができます。
　このタイプの問題を解くには、分数のかけ算で解く方法を覚えてしまえばよいのですが、三角形の面積比と長さの比の関係をより深く理解するために、「なぜ分数のかけ算」で解けるのか、その解法の流れを確認しておくとよいでしょう。左の図のように、点線の補助線を入れることで、三角形ACFと三角形BCFの面積比はAF：BFとなることから、三角形ACFの面積は三角形ABCの面積のAF/AB倍、三角形AEFの面積は三角形ACFの面積のAE/CA倍、となり、三角形AEFの面積は、三角形ABCの面積の、(AF/AB×AE/CA)倍、と求めることができます。この補助線から面積比を求めるという流れは、今後も面積比の問題で多く使うことになります。解法の流れのイメージをしっかり固めるためにも、自分で補助線をひいて解く習慣を身につけておきましょう。

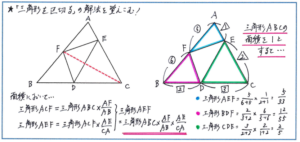
　また、比の値を間違って計算しないように、図形の中への比のかき込みを正確に速く進められるようにしておきましょう。特に、AF/AB倍とすべきところを、AF/BF倍としてしまう間違いは、相似の問題を解く際にも起こり得ることですので、注意して臨みましょう。

【第4位　流水算：静水時の速さ、流れの速さに比が使われた場合に対応できていますか？】

　流水算でも比を使った問題が範囲となるのが今回のマンスリーです。静水時の速さや流れの速さが変化する際に、比の要素が入ってくるのです。
　例えば「ある船が川を57.6㎞上るのに16時間かかりました。同じ川を、静水時の速さを1.5倍にして下ったところ、9時間かかりました。この川の流れの速さは時速何㎞ですか」と言った問題。
　川の長さも、上り下りにかかった時間もわかっているので、解答の材料は十分にそろっていますが、ポイントとなるのは、「静水時の速さが1.5倍になった」というところです。ここですぐに、上りの際の静水時の速さをマル2（メルマガでは丸の中に数字の表記が文字化けする可能性がありますため、このような表記とします）、下りの際の静水時の速さをマル3とおけるようになることが、このタイプの問題を速く正確に解くために必須となります。この、数値をマルで記号化する解き方は、来月のマンスリーの範囲となる相当算・倍数算などでも多く使いますので、早めに慣れておきましょう。
　上り、下りの速さをマルでおき、変わらない流速を含めた式を立てれば、あとは式どうしの足し算をすることで、流速を消すことができます。これは同じ流速の川での「出会いの旅人算」でも使う考え方です。数値を記号化して、式を足したり引いたりして解き進める、という流れを確実に身につけておくことで、テスト中盤で出題される可能性の高い流水算の問題で得点できるチャンスが大きく広がります。

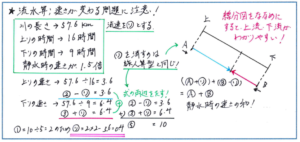
　わかっている数値が少なくても比を使いこなせれば答えを求めることができるという、比のメリットが活用できる問題のひとつです。複雑に見える問題も比を用いることで一気に解法が広がることを、しっかり認識しておきましょう。

【第5位　通過算：長さの関係を的確につかむために図を活用できていますか？】

　【第4位】の流水算と同じく、通過算でも比を使った問題が出されることがありますが、ここでも流水算の際と同じように、「マル」を使って問題内容を整理するとスムーズに正解に行き着くことができます。ただし、より確実に正解を手にするために、図を利用することがポイントになります。
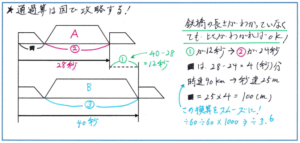
　例えば、「時速90㎞で走る電車が鉄橋Aを通過するのに、28秒かかり、鉄橋Bを通過するのに40秒かかります。鉄橋Aと鉄橋Bの長さの比は2：3です。この電車の長さは何mですか」といった問題。電車の速さも、2つの鉄橋を通過するのにかかる時間もわかっているので簡単に解けると思っていると、鉄橋の長さが比でしか表されていません。通過算の難しさは「長さの扱い」の難しさにありますが、この問題ではその難しい長さが、よりによって比で表されています。このようなタイプの問題では、まず図をかくことを最初のステップとしましょう。長さの関係を把握するには図で状況を視覚化することが有効です。
　下のように2つの陸橋を通過する図をそれぞれかいて、鉄橋Aの長さをマル2、鉄橋Bの長さをマル3とすると、その差のマル1を進むのにかかった時間が、(40－28＝)12秒とわかります。ここで、鉄橋Aを通過するのにかかった28秒が、「鉄橋A＋電車の長さ」という通過算の基本中の基本に立ち返ると、電車の長さが(28－12×2＝)4秒分であるとわかります。あとは電車の速さの時速90㎞＝秒速25m（この換算をスムーズに進められるように！）に4秒をかけて、25×4＝100（m）と、電車の長さを求めることができるのです。

　同じく比を使って解くパターンでも、【第4位】でご紹介した問題では、図がなくとも式で解き進めることができますが、上記タイプの通過算の問題では図をかくことが細かなミスを防ぎ、速く正確に正解に行き着くために必要になります。くり返しになりますが、通過算では長さをどれだけ正確に解答要素として活用できるかが得点の分かれ道になります。速さや時間と比べても長さは図で視覚化しやすいので、ぜひ図で問題内容を整理する練習を重ねておきましょう。図をかく際には、言うまでもなく、電車や鉄橋の図はできる限り単純に、車輪や窓などかかないように注意してください。制限時間内に図をかいて解くことができるように、自分にとって見やすく間違いのない図をかく練習を重ねておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。