メールマガジン宝箱 Mail magazine

　5年生最後の組分けテストです。このテストは今までの組分けと比較して難度がグッと上がります。5年の夏以降に、「速さ」や「平面図形」などの重要単元を学習してきたからです。しかし、冬期講習で忙しくテスト対策に時間をあまり割けないはずです。そこで、幅広い範囲の中でも特に出題頻度が高く、注意すべき単元を中心に、1月度組分けテストの対策ポイントを第1位から第5位までランキングにしました。ぜひ効率的に対策をしてテストに臨んでださい！応援しています！
　さらにこちらの算数予想問題と組み合わせれば、組分けテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　速さの問題：問題に合わせて線分図とダイヤグラムを使い分けられていますか？】

　組分けテストでは「速さ」の単元から難度の高い問題がテスト終盤に出される傾向があります。その難度の高さは、複雑な計算が求められるというよりもむしろ、長い問題文から内容を正確に把握する力が試される点にあります。一見複雑な問題文を正確に読み解くために必要なのは状況図（線分で動きを示す図）やグラフになりますが、問題内容に応じてどのような図・グラフを選べばよいのか、その判断をスピーディーに行うことが問題攻略のポイントになります。特に旅人算は、通過算や流水算と比べても問題のバリエーションが豊富なだけに、どのように状況図・グラフを使うかで迷ってしまいがちです。この出題パターンであればこのタイプの線分図（グラフ）を使う、といった定型こそありませんが、状況図・グラフそれぞれのメリットをおさえておくと、どちらを使うかの判断がしやすくなります。
　状況図は、グラフと比べて作図がしやすいうえに、例えば離れた地点にいる2人が向かい合って出会う場合や、同じ地点から出発して一方が折り返して出会うといったパターンで効果を発揮します。ここで前提となるのが、速さが一定であることです。動く途中で速さが変わる様子を状況図で表すことは困難ですし、図が複雑になり過ぎます。
　一方のグラフは、状況図より作図に手間がかかりますが、速さが途中で変わったり、一方が途中で休むといった、「一定ではない動き」を視覚的に把握する際に大きな効果を発揮します。またバスのように定期的に往復運動をする状況を表す際にも、グラフ（ダイヤグラム）を使うと、動きが正確に把握しやすくなります。

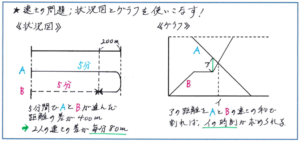
　組分けテストの難問レベルになると、図・グラフなしで解こうとすると難度は高まるばかりで、得点のチャンスも大きく減ってしまいます。例えば小問3題で構成される大問であれば、図・グラフなしで解答できるのは(1)に限られるケースが多いのに対し、少し手間はかかっても図・グラフをかいておきさえすれば、解答できる小問が一気に増えます。限られた時間内に問題内容を図・グラフで整理する時間を少しでも短縮させるために、普段から作図する練習を重ねておきましょう。

【第2位　平面図形：面積の公式を問題に合わせて柔軟に使いこなせていますか？】

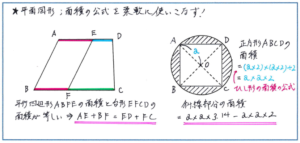
　平面図形から組分けテストの出題対象となる単元は多々ありますが、特に注意して頂きたいのが、面積を求める際に、ひとつの解法にこだわらずに、問題の内容に合わせて公式を使いこなすことです。特に下に示したような「平行四辺形の面積を台形の公式で解く」パターンと、「正方形の面積をひし形の公式で解く」パターンは、今回の組分けテストに限らず、入試問題でも頻出の解法ですので、この機会にしっかり復習して、使いこなせるようにしておきましょう。
　「平行四辺形の面積を台形の公式で解く」パターンは下のような「面積が同じになる」というケースだけでなく、台形の面積と平行四辺形の面積の比が与えられた状況で長さを求めるケースでも使えることが多く、これから面積比の問題が多く出されるに連れて、その重要性がさらに増して行きます。
　「正方形の面積をひし形の公式で解く」パターンも、今後のテストで多く使う解法です。このタイプの問題を見た瞬間に対角線を使った解法を思い浮かべられるようにしておくと、解答時間を大きく短縮させることができ、テスト全体の時間の使い方を組み立てやすくなります。
　難問が次第に多くなってくる6年生のマンスリー・組分けテスト対策において、面積の公式を柔軟に使いこなせるようになっておくことは、大きなアドバンテージになります。

　組分けテストでは中盤に、今回ご紹介したような解法をフル活用する「図形の小問集合」が出される可能性が高くあります。問題の難度自体は高くありませんが、そこで解答にかける時間を短縮させることが、後半の難問で少しでも多くの小問を解くための時間の確保につながります。問題を見てすぐに面積を求める最適の方法が思い浮かぶように、解法をしっかり確認しておきましょう。

【第3位　規則性：小問を解き進めて規則をつかみ、計算と書き出しを正確に使い分けましょう！】

　組分けテストの中盤以降の大問で出される規則性の問題は、単純な等差数列のようなシンプルな問題構成ではなく、群数列や分数の数列、そして図形を使った規則性の問題といった、見た瞬間は複雑に感じられるタイプの問題が多くなります。
　そうした複雑に見える問題に対しても、まずはひるむことなく、落ち着いて向き合って行きましょう。ポイントになるのは、最初の小問(1)です。サピックスのテストにおける規則性の問題では、まず(1)で規則を把握させ、(2)以降にその規則を使って計算を使って解答させる問題が並ぶパターンがほとんどです。それだけに(1)には特に慎重に、ミスがないように取り組む必要があります。
　そして計算を使って問題を解く段階になった際には、「あまり」の部分の取り扱いに注意しましょう。下の問題の(2)では、「はじめから数えて60番目の分数」を求めるにあたって、分数の群数列について、各組に含まれる分数の個数が、第1組が1個、第2組が2個、第3組が3個…と、組と分数の個数が一致するという規則があることから、1＋2＋…＋9＋10＝55より、60番目の分数が「第11組の5番目」であることがわかります。この「5番目」を取り違えないように気をつけなくてはいけません。そして最後は、1/11、3/11、5/11、7/11、9/11と実際に5個の分数を書き出せば正解に行き着くことができます。

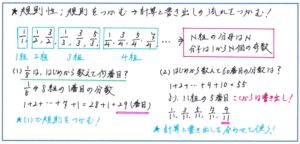
　このように、(1)を解くことで規則性を正しく把握する→計算で解き進める→最後は書き出して答えを導き出す、といった解答の流れをしっかりつかんでおくようにしましょう。今回ご紹介したようなタイプの問題以外でも、規則性の問題で使うケースが多い解法ですので、正確に使いこなせるように、練習を重ねておいてください。

【第4位　場合の数：該当するケースを正確に書き出すためのルールを守れていますか？】

　場合の数の問題では、該当するケースをもれなく挙げられるように、書き出しと計算を正しく組み合わせる力が求められます。書き出しを行う際に、闇雲に数を並べてしまうと、思わぬところでもれが発生してしまいます。問題内容に合わせたルールにしたがって書き出しを進めるようにしましょう。
　例えば、「4個のミカンを春子さん、夏子さん、秋子さんの3人で分けるとき、ミカンの分け方は全部で何通りありますか。ただし、1個ももらわない人がいてもよいものとします。」といった問題。
　ここで、春子さんが2個、夏子さんが0個、秋子さんが2個、次に、春子さんが3個、夏子さんが1個、秋子さんが0個…と、何のルールもなしに分け方を求めてしまうと、かえって解き方が複雑になり、自ずとミスが起こりやすくなります。
　そこで、「大きい数から当てはめて行く」というルールにしたがって進めてみましょう。下のように、まず4個のミカンを3人に配る個数の分け方を（a、b、c）のかたちで整理します。この際に、まずはaに当てはまる数を大きい順に4から入れて、b、cには4以下の数を入れるとして進めて行きます。aが4の場合は、b、cともに0という（4、0、0）の1つのケースしかありませんので、次にaが3の場合を考えます。aが3の場合は、残りが1個になりますので、b＝1、c＝0とします。ここでは数の組合せを挙げることが目的ですので、b＝0、c＝1のケースは含めずに、（3、1、0）として、次に進みます。aが2の場合は、残り2個を分けますので、ここでもbに当てはまる数を大きい2から始め、（2、2、0）を挙げ、さらにb＝1である（2、1、1）とします。aが1の場合は、b、cがaより大きくなってしまいますので、該当するケースはありません。
　このようにして挙げた（4、0、0）、（3、1、0）、（2、2、0）、（2、1、1）それぞれのケースについて、数の並び方を調べると、（4、0、0）は4の入る位置によって3通りに、同じく（2、2、0）、（2、1、1）も3通りとなります。（3、1、0）だけは3種類の数の並び方になりますので、3×2×1＝6（通り）となり、合計して、3×3＋6＝15（通り）と求めることができるのです。

　場合の数では、書き出しでもれが発生してしまってもそれに気づかずに解き進めてしまうことで、失点につながるケースが多く見られます。また、割合や速さの文章題のように、求めた答えを当てはめて確かめをするといった見直しもできないところに、場合の数の難しさがあります。正確にかつスピーディーに得点するためにも、ルールにしたがって書き出しをする練習を重ねておきましょう。

【第5位　基本ルールの確認：3.14計算、倍数のきまりなどを最終チェックしておきましょう！】

　組分けテストの直前までにぜひチェックしておいて頂きたい項目をここで挙げます。計算問題や文章題、図形の小問だけでなく、後半の応用問題を解き進める際に、覚えておくと時間短縮と正答率のアップを実現できる内容ばかりです。すでに覚え込むことができているお子様にとっては当たり前の項目ばかりと思われますが、忘れていると大きな失点につながってしまいますので、ぜひ最終確認をしておいてください。

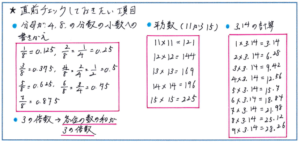
　上記にご紹介しました項目以外でも、下のような単位換算を正確にできているかもチェックしておきましょう。
・単位換算
（面積）：平方cm、平方m、a（アール）、ha（ヘクタール）、平方kmの換算
（容積）：立方cm、立方m、ℓ（リットル）、kℓ（キロリットル）の換算
（速さ）：秒速m、分速m、時速kmの換算
　特に、秒速mから時速㎞への換算では、秒速→分速が60倍、分速→時速が60倍、m→㎞が1/1000倍、といった計算の根拠を踏まえたうえで、「3.6倍」を即時行えるようにしておくとよいでしょう。
　これらの項目を忘れかけている場合は、お子さん自身に一覧表をかかせて、部屋やトイレに貼ってみることも、かなり効果的です。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。