メールマガジン宝箱 Mail magazine

　6年生最初の組分けとなる第1回組分けテストです。新6年のカリキュラムに慣れるための大事な時期でもありますが、「規則性」「平面図形」「水量の変化」など、書き出しや書き込みなど自分の手を動かして解き進める力が求められる重要単元が多く範囲に含まれる第1回組分けで、クラスアップを実現して、一気に弾みをつけたいところです。そこで、第1回組分けテストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！
さらにこちらの算数予想問題と組み合わせれば、組分けテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　平面図形：面積を求める際に、「同じ部分への移動」がスムーズにできていますか？】

　今回の組分けテストの範囲のひとつ「平面図形(1)」では、角度や面積の求め方がメインとなり、面積については、円とおうぎ形や、等積移動などの面積の求め方の工夫が主たる対象となります。5年の後期に演習した相似や面積比については、第7回の平面図形(2)で徹底的に演習するため、今回演習する範囲とは合致しませんが、この後の【第2位】で解説する「反射」では相似の考え方は利用しますし、小問集合で相似・面積比が出題される可能性もありますので、基本的な理解は見直しておくようにしましょう。
　面積の問題では、円やおうぎ形と他の図形とのが複合図形の面積の求め方や、面積が同じ部分に着目して解く「等積移動」の考え方がしっかり理解できているかを確かめる問題が出される可能性が高いです。例えば、下の図の斜線部分の合計の面積（円周率は3.14とします）はどのようにして求めればよいでしょうか。
　注意すべきは図形の上部にある中心角90度のおうぎ形の一部が円によって切り取られた「指のツメ」のような図形です。このような一部が欠けた形の場合、その部分を補う方向に考えることで解答方針が一気に立てられるケースが多くあります。この問題であれば、図形の下部にある2つの図形を矢印のように上部に移動させます。これで求める面積は中心角90度のおうぎ形から正方形を除いた部分の面積となります。
　次のステップとして、正方形の面積の求め方ですが、正方形はひし形の一部なので、ひし形の面積の公式［対角線の長さ×対角線の長さ÷2］で求められます。ここでは対角線の長さが10cmなので、求める面積は、10×10×3.14×90/360－10×10÷2＝28.5（平方cm）となります。

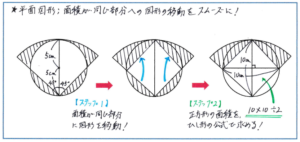
　2つ目のステップとした正方形の面積の求め方ですが、対角線の長さを使った解法は多くのケースで使われ、特に今回のような円とおうぎ形と組み合わせた図形では頻出です。円やおうぎ形の直径や半径が正方形の対角線となっていないかどうかに着目する習慣を身につけておきましょう。

【第2位　反射の問題：線対称の作図で、頂点を正しくかき入れられていますか？】

　予習シリーズ第3回の新出テーマ「反射の問題」は、先にも触れましたように相似の要素が含まれる重要単元で、出題の可能性がとても高いです。線対称の考え方を使った解き方をしっかりマスターしていれば恐れることは全くないのですが、その解き方が定着していないと、解答に時間ばかりかかり、結果として得点に至ることができないといった事態が起こりがちな要注意単元です。練習の段階では時間がかかっても、線対称を使った解き方を確実に身につけておきましょう。
　例えば、「下の図のような長方形ＡＢＣＤがあり、辺ＣＤ上の点Ｐから小球を辺ＢＣ上の点Ｐに向けて発射します。このとき、小球はまっすぐ進み、辺に当たるたびに入ってきた角度と同じ角度ではね返ります。この小球が辺ＢＣ→辺ＡＤの順に当たってはね返った後、頂点Ｂで止まったとき、ＢＰの長さは何cmですか」といった問題。ここで大前提となるのが、「辺ＢＣについて長方形ＡＢＣＤと対称な図形を作ると、はね返る小球の動いた線は、直線で表すことができる」という点です。下の左の図のように、線対称で作図した長方形をＢ(Ａ)(Ｄ)Ｃ、辺ＢＣではね返った小球を表す線ＰＱを線対称で作図した線をＰ(Ｑ)とすると、角ＥＰＣ＝角ＱＰＢ、角ＱＰＢ＝角(Ｑ)ＰＢより、角ＥＰＣ＝角(Ｑ)ＰＢとなり、対頂角が等しくなるため、点Ｅ、点Ｐ、点(Ｑ)は一直線上にあることになります。
　この考え方を使って、右の図のように、小球が当たった辺について線対称な図形を次々に作っていくと、小球の動く様子は直線Ｅ(Ｂ)として表すことができます。ここで、三角形ＥＣＰと三角形(Ｂ)ＢＰは相似となるため、ＣＰ：ＢＰ＝ＣＥ：Ｂ(Ｂ)＝(9－3)：(9×2)＝6：18＝1：3となります。よって、ＢＰの長さは、18÷(1＋3)×3＝13.5（cm）となります。

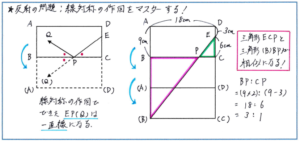
　反射の問題の中には線対称の考え方を使わなくても解答できる問題があります。線対称の作図には手間と時間がかかることは避けられませんので、問題をよく読み込んで、線対称の作図が必要かどうかの判断をするようにしてください。それでも、線対称の考え方を使いこなせれば、どのような問題にも対応することができますので、テスト会場で極力時間をかけずにスムーズに作図ができるように、線対称の図形を正確にかく練習を重ねておきましょう。

【第3位　集合算：ベン図をかいて計算式を立てる解法の流れをマスターできていますか？】

　集合算では問題内容をベン図で正しく整理して、計算式を立てるという流れを速やかに進められるかどうかが得点のポイントになります。ベン図のかき方自体は難しいものではありませんが、問題文を読み込み、ベン図から「重なり」の部分に注意して計算式を立てる作業を正確に進められているかどうか、注意して進める必要があります。
　例えば、「50人のクラスで算数のテスト行いました。問題は3題あり、問1が2点、問2が3点、問3が5点の10点満点です。（図1）はその結果をまとめたものです。このテストで、1問だけ間違えた生徒は全部で28人でした。このとき、問3を正解した生徒は何人いますか」といった問題にはどのように取り組めばよいでしょうか。

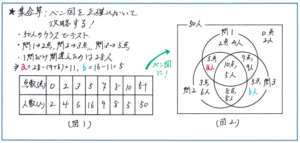
　(図1)をベン図にしたものが右の（図2）です。ここで注意すべきは、「5点」の場所が2か所あることです。5点の人数のうち、問1と問2を正解した人をa人、問3だけ正解した人をb人としています。また、「1問だけ間違い」という条件を見逃さないように注意しましょう。問1だけを間違えた人の点数は、3＋5＝8(点)、問2だけを間違えたの人数は、2＋5＝7(点)、問3だけ間違えた人の点数は、2＋3＝5(点)になります。
　以上より、a＋9＋8＝28となり、a＝11(人)とわかります。また、5点の人は16人いますから、b＝16－11＝5(人)となり、問3を正解した生徒は、5＋8＋5＋9＝27(人)と求めることができます。
　3つのベン図は、2つに比べると練習する機会が少ないので、重なっている部分が何を表しているかに注意してしっかり練習をしておきましょう。

【第4位　水量・水深の変化：容器を断面で見て考える解法を使いこなせてていますか？】

　水量・水深の変化の問題の得点力を上げられるかどうかは、断面図をかいて解き進められるかどうかで決まります。複雑な問題になればなるほど、問題内容を断面図で整理して考える力が求められます。まずは簡単な問題で図に状況をまとめる練習をして、応用問題でも図がかけるような力を養成しましょう。
　例えば、次のような問題。「底面の半径が15cmで、高さが20cmの円柱の形をした容器に、深さ8cmまで水が入っています。この中に底面の半径が9cmで、高さが20cmの円柱の形をしたおもりを底にまっすぐに立てました。その後、おもりをまっすぐに4cm引き上げると水の深さは何cmになりますか。ただし、円周率は3.14とします」といった問題で、断面図を正確にかけるでしょうか。
断面図では、縦の長さを「高さ(深さ)」に、横の長さを「底面積」とします。ここで注意すべきは、「円周率を使わずに解くこと」です。円周率3.14が含まれると、計算が一気に複雑になってしまいます。問題の条件にあるからといって円周率を使う必要はありません。
　円周率の代わりに使うのは「比」です。底面の円の相似比は 容器：おもり＝15：9＝5：3です。よって底面積の比は 容器：おもり＝(5×5)：(3×3)＝25：9 となります。
　ここで、はじめの状況を断面図に整理すると下の(図1)になります。比を使って水の量を表すと マル25×8＝マル200 となります。水の量も実際の値ではなく、比を使って水の量を決めることが重要です。
　次におもりを入れた後の状況を断面図に整理すると(図2)のようになります。容器の底面積をマル25、おもりの底面積をマル9とかき込みますが、ここで注意して頂きたいのが、おもりの位置を左か右に寄せてかくことです。水が入っている部分の底面積が マル25－マル9＝マル16 とわかるので、水の深さは マル200÷マル16＝12.5(cm)と求めることができます。
　そして、おもりを引き上げたときの状況を断面図に整理すると(図3)のようになります。ここで下から4cmは底面積がマル25の部分に水が入り、それより上では底面積がマル16の部分に水が入っていることがわかります。アの部分の水の量は マル25×4＝マル100 となるので、イの部分の水の量は マル200－マル100＝マル100 と計算でき、底面積がマル16なので、シカク＝マル100÷マル16＝6.25(cm) とわかります。したがって、水の深さは 4＋6.25＝10.25(cm) となります。最後に4cmを足すことを忘れないように注意しましょう。

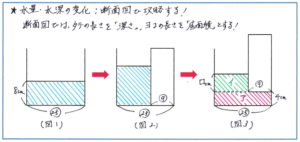
　このように基本的な問題で断面図のかき方を練習していけば、沈めるおもりが複雑になったり、おもりを複数沈めたり引き上げたりした問題でも対応できる力が大きくアップします。繰り返し練習して確実に身につけていきましょう。

【第5位　日付の問題：どこを起点に日数を数えるかで迷うことはありませんか？】

　数と規則性の中でも「日付」に関する問題は、苦手とするお子様がとても多い単元です。問題の種類は限られており、問題文自体は複雑ではないのですが、月によって30日か31日か（あるいは28日か29日か）という場合分けが必要になること、そして、日数を計算する際に「その日を含むかどうか」といった、数え始める起点まで考えなくてはいけないことといった、処理しなければならない情報が想定よりも多い点が、問題を難しく感じさせています。
　例えば次のような問題には、どのように対応すればよいでしょうか。「ある年の8月の火曜日の日付の合計は66でした。この年の5月15日は何曜日ですか。」
　まずはこの年の8月の火曜日が4週あるか、5週あるかの確認が必要になります。ここは『予習シリーズ算数6年上』の25ページに掲載された解説の通り、線分図をもとに、火曜日が5週あるとすると、火曜日の日付の合計が最小でも1＋8＋15＋22＋29＝75となることから、この年の8月の火曜日は「4週」と定められます。この流れは、日付に関する問題を解く上で必須になりますので、しっかり習得しておきましょう。第1火曜日をシカク1として、シカク1＋（シカク1＋7）＋（シカク1＋14）＋（シカク1＋21）＝66より、シカク4＝66－42、シカク1＝6となり、8月の第1火曜日が8月6日と求めることができます。
　8月の曜日構成を把握した上で、5月15日の曜日を求めるにあたって、5月15日を起点として8月6日の火曜日までの日数を計算する方法もあるのですが、期間の終点の8月6日の曜日がわかっている状況で計算を進めるので、曜日をさかのぼるかたちで解き進める方がよいでしょう。より確実に曜日を把握するために、簡単にまずカレンダーをかいて、8月1日が木曜日であることを踏まえます。7月31日から5月15日までの日数は、31＋30＋31－14＝78（日）となり、7月31日の水曜日から、[水・火・月・日・土・金・木]という周期で考えます。78÷7＝11あまり1より、5月15日は「水曜日」と求めることができます。

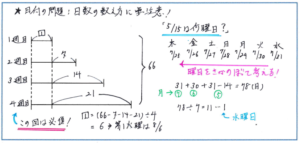
　日付の問題は、計算そのものはいたってシンプルなのですが、日数の数え方やどの日を起点にするかを曖昧にしてしまうと、得点のチャンスを逃してしまいます。この問題の8月1日が木曜日であることを求める際に簡単にカレンダーをかいたように、手書きの作業を織り交ぜながら、規則性を求める練習を重ねておきましょう。

われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。