メールマガジン宝箱 Mail magazine

　4月度マンスリーテストは、マンスリーとはいえ春期講習で演習した単元すべて、さらに「速さ」まで加わる、とても範囲の広いテストです。しかも図形やグラフ、規則性などの重要単元が勢ぞろいしますので、どこから復習を進めればよいか迷ってしまうところです。それでも、ポイントさえしっかりつかめれば、クラスアップのチャンスは十分にあります。そこで6年4月度マンスリーテストの対策ポイントを第1位から第5位までランキングにしましたので、ぜひマスターしてテストに臨んでださい！応援しています！
さらにこちらの算数予想問題と組み合わせれば、組分けテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　平面図形：有効な補助線を引くことはできていますか？】

　平面図形の問題では、図形の中から「相似」と「高さ共通の図形での面積比は底面比と等しい」という2つの要素を的確に見つけ出すことがポイントになりますが、問題の難度が次第に上がってくると、ただ与えられた図形を見ているだけでは要素の見つけ出しが上手く行かなくなります。
　そこで必要なのが補助線です。補助線によって新たな相似の関係を作り出すこと、面積比を利用しやすいかたちにすることが可能となり、正解への道筋がはっきりと見えてきます。例えば下のような、三角形ABCの中の三角形AEFと三角形BDFの面積、そしてAE：CEとBD：CDが与えられた状態で、AF：BFを求めさせる問題の場合には、どこに補助線を引けばよいでしょうか。求めるのはAF：BFなので、AFとBFをそれぞれ底辺として高さが等しい、三角形ACFと三角形BCFの面積比が求められればよいことがわかります。そこで、CとFを線で結んでみましょう。AE：AC＝4：(4＋3)＝4：7より、三角形ACFの面積は、24×7/4＝42（平方cm）、BD：BC＝2：(2＋5)＝2：7より、三角形BCFの面積は、36×7/2＝126（平方cm）となるため、AF：BF＝(三角形ACFの面積)：(三角形BCFの面積)＝42：126＝1：3と求められます。

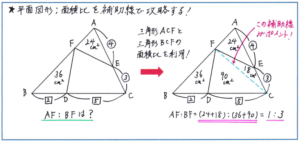
　補助線を引く際にまず注意すべきは、相似や面積比の基本パターンを活用できるかたちにすることです。今回ご紹介した問題でも、面積比＝底辺の長さの比というパターンが習得できていれば、三角形の面積比を利用するという考え方をすぐに思い浮かべることができます。相似でも、相似の基本パターンを作り出すことを念頭に置けば、補助線が断然引きやすくなります。SAPIXのテストでは、これから図形の問題の難度がどんどん上がってきますが、基本パターンさえ把握できていれば、そうした難問でもしっかり攻略できるようになります。相似、面積比の基本パターンが理解できているか、確認を徹底しておきましょう。

【第2位　グラフ：問題文の内容を正しくグラフに書き入れられていますか？】

　グラフの問題の中には、あらかじめ問題でグラフが提示されないケースがあります。特に速さの問題では、水深変化など他のグラフを使う問題と比べて、グラフなしの状態で解かなければならないケースが多くあります。そうした問題で着実に得点するには、問題文で示された情報を的確にグラフの中に書き込み、速さ、時間、距離の関係を式で表す作業が必須になります。
　例えば、「A君は普段、家から学校まで分速50mで歩いて行きますが、ある日、家を出発してから12分までは分速50mで歩き、12分後からは分速150mで走ったところ、普段よりも2分早く学校に着きました。家から学校までは何mありますか」といった問題。グラフを使って問題内容を整理すると、下のようになります。ここで、グラフ上の速さを変えた点をP、速さを変えた日に学校に着いた点をQ、分速50mで普段通り進んだ場合に学校に着く点をRとします。速さを変えた地点から学校までの距離は同じですので、P→Qを進むのにかかる時間と、P→Rを進むのにかかる時間の比は、速さの比の逆比である、1/150：1/50＝1：3となります。この比の差（3－1＝）2が2分にあたりますので、普段の通りの分速50mでP→Rを進んでいれば、家から学校までは、12＋2÷(3－1)×3＝15（分）かかることがわかります。よって、家から学校までの距離は、50×15＝750（m）と求められます。

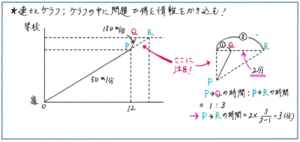
　「普段通りの速さ」で進んでいた場合を想定してグラフに線を書き入れる作業が難しいように感じられるかもしれませんが、問題で「普段よりも2分早く学校に着いた」とありますので、この情報を何とか活用しなくてはなりません。そう考えると、グラフに普段通りの動きを書き入れるという作業は、どうしても必要なものです。グラフを使いこなせると、これまで習ってきた速さと比の考え方を視覚的に取り込むことができます。ますはグラフをかくという作業を面倒に思わずに練習を重ねてください。慣れるとグラフはどんどんスムーズにかけるようになります。

【第3位　規則性：規則性を見つけやすくするために「区切り方」に注意しましょう！】

　規則性の問題で難度がアップすると、どこまでを書き出し、どこから計算に持ち込むかの判断が難しくなります。特に図形や数表を使った問題になると、簡単に書き出しを進められないケースが出てくるため、規則性をスムーズに見つけることが困難になります。そこで大事になるのが、「区切り方」です。
　例えば下の図のような、マス目に書かれた数字が中央から「らせん」のかたちで大きくなって行くようなかたちで、5×5のマス目の1列目の1行目（左上端）の数字を求める場合を題材として考え方を整理してみましょう。実際に書き出してみると、求める数字は17となります。ここで、すべての数を書き出さずに求める方法を考えます。マス目の最も外側に並ぶ数に着目します。外から2つめの周に並ぶ数で最も大きい値は（3×3＝）9となります。そこで最も外側の周を4つの等しいブロックに分けると、1つのブロックには4つの数が入ることがわかります。そこで求める左上端の数は、9にブロック2つ分の4×2＝8を加えて、9＋8＝17と求めることができます。
　5×5＝25（個）であれば、数字を全て書き出してマス目をうめても時間のロスは少ないですが、それが11×11のように大きくなってしまうと、書き出しに時間がかかり過ぎてしまいます。ブロックに分ける方法で考えれば、外から2つめの周に並ぶ数で最も大きい値が（9×9＝）81、最も外側の周の1つのブロックに入る数字は（11－1＝）10のため、81＋10×2＝101とスムーズに答えに行き着くことができます。

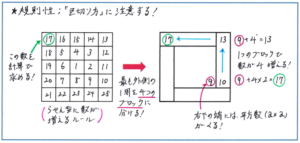
　規則性の問題で書き出しは重要な解法です。ただし、求める数字が大きくなる場合には、書き出しに頼り過ぎてしまうと時間がかかるうえに正答率も下がる危険性があります。ルールをつかむために書き出しを行ったうえで、計算を使って解答に行き着く、という流れが、SAPIXのテスト後半に出される規則性の問題を攻略するポイントとなりますので、計算で解き進める練習をしっかり重ねておきましょう。

【第4位　場合の数：基本パターンの成り立ちを正しく理解できていますか？】

　場合の数の問題で解き方のパターンを習得するには、パターンの基本的な成り立ちを正しく理解しておくことが大前提で、そうした理解なしに、ただ解き方を丸覚えしようとしてしまうと、応用問題に全く対応できなくなってしまいます。
その端的な例が「最短経路」の問題です。マス目で示された道の、端から端まで最短経路で行く方法を求めるタイプの問題ですが、このタイプの問題では、マス目の端に数字を書き込んで、その和を書き連ねて行く解法が、計算を機械的に、スピード感をもって進められるメリットがありますので、必ず習得しておきましょう。
　ポイントは、この解法パターンの基本的な成り立ちをしっかり理解することにあります。問題の難度が上がり、例えば下の図のような立体図形での最短距離を答えさせる問題になった場合に正確に対応できるかどうかは、基本的な成り立ちを理解できているかどうかにかかっているのです。
　下の立体の点Aから点Kに最短距離で進む方法を求める際に、点Aから点Fに進む場合には、点A→点Bから進む1通りと、点A→点Eから進む1通りを合わせて2通りとなります。さらに、点Aから点Gに進む場合には、点Fから進む2通りと点Hから進む2通り、そして点Cを経由して進む方法は、点A→点Bから進む1通りと、点A→点Dから進む1通りの合わせて2通りなので、すべて合わせて6通りとなります。この考え方にそって、点Aから進む場合の数を各点に書き込み、その和を書き進めて行くと、点Aから点Kまで進む方法が、12通りあることがわかるのです。

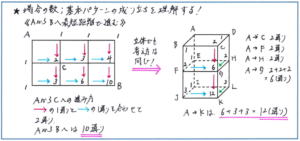
　平面図形での最短距離の求め方が、成り立ちから理解できていれば、立体図形での最短距離のような応用パターンにも適切に対応することができますが、ただ、「点に数を書き入れて足して行く」とだけ覚えてしまうと、数の書き入れ方に安定を欠き、得点に至らない可能性が高くなります。得点のチャンスを大きく広げるためにも、パターンの基本的な成り立ちを習得しておくようにしましょう。

【第5位　流水算・通過算：問題内容を図を使って正しく整理できていますか？】

　春休み前に演習した流水算・通過算の単元からは、長い文章で構成され、内容の整理が難しい問題が出される可能性が高くあります。そうした問題を攻略するためには、図で内容を整理する作業が不可欠です。例えば、通過算で次のような問題には、どのように対応すればよいでしょうか。
　「長さ135mで秒速25mの電車Aと、長さ225mで秒速35mの電車Bがあり、花子さんが2つの電車が走る線路と並行する道を走っています。花子さんの真横で電車AとBがすれ違いはじめ、花子さんの真横で電車Aと電車Bがすれ違い終わりました。花子さんは秒速何mで走っていましたか」
　単に電車AとBがすれ違う、あるいは追いこすといった基本パターンであれば、あえて図をかかなくても式を立てるのに大きな負荷はかからないでしょう。この問題では、そこに花子さんという要素が加わることで、難度が一気に上がっています。そこで図をかいて問題内容を整理するのですが、まずは電車AとBがすれ違いはじめてからすれ違い終わるまでの様子を図にして、そこに花子さんの動きを加えることにしましょう。この問題に限らず、まずは整理しやすい要素から図にすると、複雑な内容でも表しやすくなります。

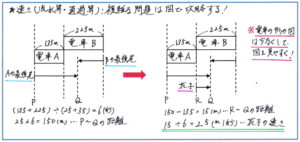
　通過算で図をかく際に、電車の図をどこまで盛り込むか迷ってしまうところですが、この問題で2つの電車がすれ違いはじめた時点と、すれ違い終わる時点の両方で電車の図をかき込んでしまうと、図が複雑になってしまいます。花子さんの動きもかき込むので、電車の動きはできるだけシンプルにしておくようにしましょう。そこで電車AとBがすれ違いはじめる時点の様子を表す際に、2つの電車の先頭が重なるように、電車の図を使うことにします。すれ違い終わる時点については、2つの電車の最後尾の動きを矢印で表せばよいでしょう。
　そこに花子さんが走る様子を図にかき込みますが、2つの電車がすれ違いはじめる時点で、電車の先頭どうしが重なる地点から花子さんが動きはじめ、最後尾どうしが重なる地点で動き終わるように、矢印をかき入れます。
　こうして上の右側の図のように問題内容が整理できれば、正解まであと少しのところまで解き進められています。電車AとBがすれ違いはじめてからすれ違い終わるまでにかかる時間は通過算の基本中の基本の式で、(135＋225)÷(25＋35)＝6（秒）と求められます。この6秒間で電車Aが進む距離は、25×6＝150（m）で、図より、花子さんが6秒間で進んだR～Q間の距離は、150mから電車Aの長さ135mを引いて求められます。よって、花子さんの速さは、(150－135)÷6＝2.5（m/秒）より、秒速2.5mと求められます。
　今回ご紹介した問題であれば、たった3つの式で正解に行き着くことができます。複雑に見える問題でも、図で内容が整理できれば、図のどの部分を求めればよいかが視覚的に把握でき、多くの式を使うことなく解き進められます。特に速さの問題は視覚的に内容を把握することが必須となります。図をかく練習をしっかり重ねておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。