メールマガジン宝箱 Mail magazine

　6月度マンスリーテストは、特に相似や変化のグラフなどで、これまで習ってきた解法を速く正確に組み合わせて解く力が試される問題が多く出されます。偏差値アップのポイントは、各単元の基本的な解法を正確に使いこなせるかどうかという点になります。解法の基本さえしっかり理解できていれば、問題内容が複雑になっても、解答方針を立てることができ、得点のチャンスを大きく広げることができます。

　そこで解法の組み合わせに注目して、6年6月度マンスリーテストの対策ポイントを第1位から第5位までランキングにしましたので、ぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの算数予想問題と組み合わせれば、マンスリーテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　平面図形（四角形と面積比）：相似→底辺比の「視点の切り替え」はできていますか？】

　今回のマンスリーでは、平面図形の相似の単元から難度の高い問題が出される可能性が高くあります。特に平行四辺形や長方形、台形といった平行な辺を含む四角形の中に何本かの線が書き込まれた図から、相似の関係を見つけ出して、面積や長さを求める問題は、解法によっては必要以上に多くの時間を費やしてしまうことになります。難度の高い問題で少しでも得点をかせぐために、図形のどこに注目すればよいのかという「相似を見つける目」をしっかりと養っておく必要があります。

　相似の中でも「砂時計型」と「ピラミッド型」といった基本パターンをしっかりと踏まえたうえで、その関係から求められた比が、別のかたちで活用できないか、といった「視点の切り替え」ができるようになると、正解できる問題の幅が一気に広がります。

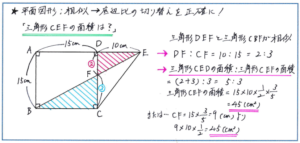
　例えば下の図であれば、四角形ABCDが正方形であることから、AFとBCが平行になり、三角形DEFと三角形CBFが相似になるところまでは、すぐに進めるでしょう。なお、メルマガでは分数を「分子/分母」のかたちで表記します。

　ここで相似比から、DF：CF＝2：3が求められれば、あとは、三角形CEDの面積と三角形CEFの面積の比が、底辺の長さの比の5：3になることを利用して、三角形CEFの面積＝三角形CEDの面積×3/5＝15×10×1/2×3/5＝45（平方cm）としてもよいですし、CFの長さが、15×3/5＝9（cm）になることから、底辺をCF、高さをDEとして、三角形CEFの面積＝9×10×1/2＝45（平方cm）の方法でも正解に行き着くことができます。

　マンスリーでは、今回ご紹介した基本レベルの問題から難度がさらに上がり、複雑に図形が組み合わさった問題が出される可能性が高いですが、視点の切り替えを意識して図形を見れば、解法の糸口が見つけやすくなる点は変わりません。普段の演習でも正解したかどうかだけではなく、図形のどの部分に注目すればよかったのか、そのプロセスを必ず見直すようにしましょう。その積み重ねが「相似を見つける目」の養成につながります。

【第2位　変化のグラフ：断面図を使った比の解法は身につけられたいますか？】

　「変化のグラフ」の中でも、容器に水を入れた時間と水の深さの関係を表すグラフを題材とした問題は、立体図形の成り立ちを正確に見抜く力を求められる点で、難度が大きく上がります。もともと立体図形の問題は平面図形と比べてイメージがつかみづらいうえに、グラフを組み合わせた問題になると「変化の様子」まで細かく把握しなければならなくなるため、対応が難しくなります。この変化をいかにわかりやすくとらえるかが、水深変化とグラフの問題での正答率アップにつながります。

　具体的な対策として、容器の断面図を利用する方法を使いこなせるようにしておくと、対応できる問題の幅が大きく広がります。立体図形の問題では、容器に水を入れる問題以外にも、おもりを沈めるような問題でも断面図を利用するケースは多く、これまでの演習で断面図をかくこと自体は十分に演習を重ねてきたと思われますが、さらにそこから比を有効活用できるようになれば、グラフとの関係をしっかりつかめるようになります。

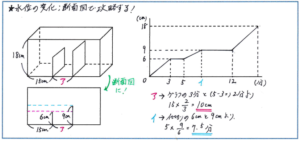
　例えば上の図のように、直方体の底辺に垂直な仕切りが2枚立てられた容器に一定の割合で水を入れた際の、時間と底辺Ａの部分の水の深さの関係を表したグラフを参考に、容器のアの長さと、グラフのイの時間を求めるような問題。

　このタイプの容器とグラフの関係はこれまでも何度か出題されてきましたので、底面積の変化に合わせてグラフの形状が変わることはスムーズに理解できると思われますし、仕切りの高さもグラフから容易に求められるでしょう。そこで底面積・仕切りの高さとグラフの関係を「比」を利用して深く理解するためには、断面図が非常に有効です。

　変化とグラフの問題では、変化の様子をどれだけ正確にイメージできるかがポイントになります。そこで、断面図をかいたり、グラフに書き込みをするといった手作業を加えることは、イメージを視覚的に持つ効果が望めます。制限時間のあるテストで作業を効果的に進めるには、どうしても慣れが必要ですので、普段から手を動かして作業を進める意識を持って演習を進めましょう。

【第3位　3つのつるかめ算：選び出しにもれがないように、面積図と表を活用できていますか？】

　「不定方程式」については、新6年2月度マンスリーでも範囲となりましたが、今回のマンスリーでも場合の数のひとつの単元としてテスト範囲に含まれます。まずは「1本60円のえんぴつと1本90円のボールペンを何本か買ったところ、代金は750円になりました。えんぴつを何本買いましたか。考えられる本数をすべて答えなさい」といった基本パターンについては、すぐに解答方針が立てられるように復習を徹底しておきましょう。

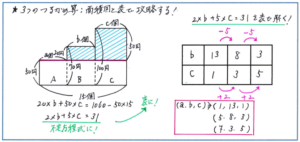
　今回のその基本パターンを踏まえて、不定方程式の考え方を使った、「3つのつるかめ算」といった応用問題が出される可能性が高くあります。例えば、「1個50円の品物Ａ、1個70円の品物Ｂ、1個100円の品物Ｃを合わせて15個買ったところ、代金は1060円でした。このとき、品物Ａ、Ｂ、Ｃはそれぞれ何個ずつ買いましたか。ただし、どの品物も1個は買ったものとします。」といった問題。

　合計個数と合計代金がわかっているので、つるかめ算の基本的な解法で解けそうですが、このままでは、つるかめ算の式を立てることができません。ここでポイントになるのが、最後に示された「どの品物も1個は買ったものとする」という点です。それぞれの個数は分からないものの、下の左のような面積図をかくことができます。そこから、50円のラインで面積図を切って、ラインから上の部分に注目すると、「(70－50)×b＋(100－50)×c＝1060－50×15」という式が成り立ちます。

　式を整理すると、「20×b＋50×c＝310」から「2×b＋5×c＝31」という式を導くことができるため、あとは不定方程式の基本的解法で表を使えば正解に行き着くことができますが、ここで「b＋cが15より小さいこと」「b、cともに0にならない」ことを条件とすることを忘れないように注意しましょう。

　不定方程式のように「すべて答えなさい」と指示のある問題は算数に限らず全教科のテストにおいて、お子様方が苦手とされていると思われます。答えが1つに定まらないことで、問題の難度が大きく上がるように思われるかもしれませんが、不定方程式は解法さえ覚え込めば、決して難しい問題ではありません。面積図や表といった視覚的に理解を促す道具を使いこなして解き進める練習を重ねましょう。

【第4位　規則性に関する問題：等差数列の基本公式を正確に利用できていますか？】

「規則性に関する問題」でも、これまでに習った等差数列に関する式など、基本的な要素を的確に使いこなして解かせる応用問題が出される可能性が高くあります。例えば、次のような問題に正確に対応できているでしょうか。
　
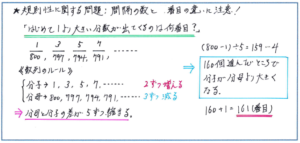
「下のように、ある規則にしたがって分数が並んでいます。
　　1/800、3/797、5/794、7/791、…
　このとき、はじめて1より大きい分数が出てくるのは左から数えて何番目ですか。」

　デイリーサピックスでも出てくる分数列の典型題のひとつですが、注意深く進めなければ、思わぬところで得点のチャンスを逃してしまいます。まず数列の規則ですが、分子を見ると、1、3、5、7、…と、1から始まり2ずつ数が増え、分母は、800、797、794、791、…と、800から始まり3ずつ数が減っていることがわかります。

　問題にある、「はじめて1より大きい分数が出てくる」という状況ですが、分数が1より大きいということは、「分子が分母より大きくなること」を意味します。1番目の分数の分子は1、分母は800で、ここから分子は2だけ増え、分母は3だけ減りますので、ひとつ順番が進むごとに分子と分母の数の差が2＋3＝5ずつ縮まることになります。この考え方は、速さの旅人算に近いもので、「はじめの差を、1回に縮まる差の5で割る」という方針が成り立ちます。

　式にすると、(800－1)÷(2＋3)＝799÷5＝159あまり4となります。ここからがポイントで、意外な落とし穴がありますので注意して臨みましょう。式から導き出した「159あまり4」が何を表すかを確認します。これは、最初の1/800という分数から、159＋1＝160（個）「進んだところで」、はじめて分子が分母より大きくなる、ということです。求めるのは、「何番目の分数か」ですので、160に1を足して、161番目と答えなくてはなりません。ここで焦って160番目としてしまわないように、徹底的に注意してください。

　規則性の問題で注意すべきは、「どこまで書き出し、どこまでを計算で処理するか」の判断に迷う時間を作らないことです。制限時間のあるテストでは速く正確に解き進めることが求められますので、書き出しに使える時間には限りがあります。すべてを調べるのではなく、規則性を正しく見つけるための書き出しを行うという目的から逸脱しないよう、必要最低限の書き出しで解き進められるように、練習を重ねておきましょう。

【第5位　場合の数（投票算）：仮の競争相手を立てる式の意味を確実に理解できていますか？】

　「場合の数」の中に含まれる「投票算」は、解き方を正確に身につけておけば確実に得点源にできますが、少しでも理解が曖昧にしてしまうと思わぬミスにつながる要注意単元です。式のかたち自体は単純ですが、理解が不足していると式の立て方そのものを間違えてしまうのです。

　例えば、「ある中学校の生徒360人が1票ずつ投票して4人の委員を選ぶ選挙をします。投票は1人の名前だけを書き，無効票はないものとします。何票以上投票されればその人の当選が確実になりますか。ただし，立候補者は5人以上はいるものとします。」という問題。

　基本パターンにあてはまるこの問題では、「360÷5＝72、72＋1＝73」の式より、正解は73票となります。ここで全校生徒数360を「4」ではなく「5」で割ることがポイントになります。この問題では投票数の上位4名に入れば当選しますが、ここで360÷4＝90（票）と考えないように注意が必要となるのです。その理由をしっかりと確認しておきましょう。

　「360÷4」とするのは、「当選する4人以外全員の得票数が0票であること」が前提となり、「4位になるための最多の得票数」を表します。問題では「当選するための最も少ない得票数」を求めますので、4位になるためには5位の生徒より1票でも多く獲得すればよいことになります。つまり「5位の生徒という仮の競争相手」を想定して解くという方針になるのです。

　5位の生徒が得票できる最多の数が、360÷5＝72（票）ですので、4位になるための得票数は、それに1票を足した72＋1＝73（票）となります。

　「当選する人数に1を足した数で割って、1をたす」というかたちをただ丸暗記するのではなく、なぜその式になるのかを必ず確認しておきましょう。それによって暗記がより確実になるだけでなく、問題の出され方が変わっても対応できるようになります。解法の理由がわかっていれば、決して難しい問題ではなく、確実に得点しておきたいのが投票算です。曖昧な理解になっていないか、式の立て方を再度確認しておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。