メールマガジン宝箱 Mail magazine

　今回の組分けテストでは、「立体の切断」や「平面図形の移動」といった、自分で作図をし、図にかき込みをして、そこから解答方針をいかに速く立てられるかを試す問題が多く出されます。組分けテストも第3回をむかえ、問題の複雑さが増してくる中で、制限時間内に図を正しくかいて問題内容を理解することが高得点をとるポイントになります。正確な作図から解答を進める力が求められる、6年最後の組分けで、一気にクラスアップを実現したいところです。そこで、第3回組分けテストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの算数予想問題と組み合わせれば、組分けテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　立体の切断：切断の基本的なルールを完全習得できていますか？】

　「立体の切断」については、『予習シリーズ5年下第14回』で切断の基本的な成り立ちを学習して、今回は「2段階切断」など、応用編に進むことになります。新たなステップの学習に早く進みたいところではありますが、いま一度、切断の基本的なルールを確認しておきましょう。

　まず大原則が「向かい合う平面に入る切断の線が平行になる」ことで、この原則にしたがうことで、切断によってできる向かい合う図形の相似関係を把握することができます。図形（三角形）の相似関係さえつかめれば、主に大問の(1)で出される、切り口の面を立体の辺が交わる点の位置をスムーズに解答することができるようになります。

　さらに覚えておきたいのが、立体の相似関係を使って体積を解く流れです。入試問題でも頻出の「切断によってできる立体の体積」を求める問題では、下の図のように、「角（つの）出し」と言われる、辺や切断線の延長線の交点から「すい体」をつくる流れを利用します。ここで、大きなすい体から小さなすい体を引いて求めても、もちろん正解に至ることはできるのですが、相似な立体の体積比が、「相似比を3回かけ合わせて求められる」ことを利用すれば、かけ算の式を使うことで、計算ミスを防ぐ効果があります。

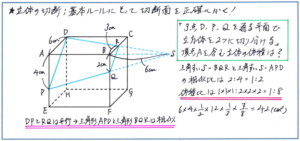
　言うまでもないことですが、立体の切断では自分で図へのかき込みや、場合によっては図を最初からかく作業が必須になります。切断線をかく時に神経質になる必要は全くないのですが、テストの際に自分でも見やすい切断面をかけるように、普段から切断線を引く練習を徹底的に重ねておきましょう。

【第2位　食塩水の混合：複雑な混ぜ合わせの問題ではやりとりの図をフル活用しましょう！】

　「割合と比の文章題」の「食塩水を混ぜ合わせる問題」で正解を得るポイントは、図の正確な使いこなしにあります。特に、「5%の食塩水200gと8%の食塩水300gを混ぜ合わせると何%の食塩水ができますか」といったシンプルな混ぜ合わせでは、面積図（天びん図）を使えばすぐに正解を得られます。もちろん食塩の量を実際に算出する方法でも解き進められますが、様々なバリエーションの混ぜ合わせに対応するためにも、面積図を確実にかけているか、この機会に最終確認をしておきましょう。

　得点差が生まれるのは、いくつかの種類の食塩水の一部をやりとりして濃度を変化させるタイプの問題です。やりとりの際の数値が導き出されば、面積図や天びん図を利用することで解答への道筋が定まります。ポイントとなるのは食塩水をやりとりした際に、濃度や食塩水の量などがどのように変化するのかを、視覚的にもわかりやすく把握することです。ビーカー図を使う方法もありますが、下のような簡単な長方形の中に、濃度・食塩の量・食塩水の量を書き込めるようにすると、やりとりのイメージがつかみやすくなります。特に変わった量、変わらない量が何かを流れの中で見て取ることができる点にメリットがあります。

　ビーカーの図も効果的ではありますが、濃度などを書き込む場所がはっきりとルール化できますので、より速く作業を進めることができます。気をつけるのは、長方形の間隔を狭くしないようにかくことです。食塩水の移動や水の注入は矢印で表し、そこに数値を書き入れますので、ある程度スペースに余裕を持たせた方が書きやすくなります。やりとりが行われた各段階では面積図や天びん図をフル活用して、正確に数値を導き出しましょう。

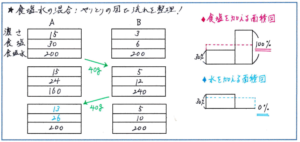
　また、面積図の使い方として、食塩のみを加える場合は「100%の食塩水」、水のみを加える場合は「0%の食塩水」とすれば、水を加えた、食塩を加えたといった作業も比を使って処理することができます。いつでも面積図を使う必要はありませんが、内容を整理するための強力な武器となる面積図のかき方をテスト前にしっかり確かめておくとよいでしょう。

【第3位　円の転がり運動：回転する円の「向き」を正確に把握するためのかき込みができていますか？】

　今回の組分けテストにおける「平面図形」の単元では、様々なパターンの「移動」が出題対象になります。長方形のまわりや内部を正三角形や円が回転移動する、直線上を直角三角形や長方形が平行移動するなど基本的なパターンに対応するには、図形が移動する様子を自分でかき込むことがポイントになります。

　また、三角形やおうぎ形が回転移動する問題でも、辺（円やおうぎ形であれば半径・直径）の動きをとらえたうえで、回転の様子を図にすることが重要で、いずれも丁寧になり過ぎない範囲で、見やすく図をかく練習が不可欠となります。

　そんな中で特に注意しておきたいのが、下の図のような、円のまわりを円が転がって移動するタイプの問題です。特に回転数を求める問題は、頭の中だけで解こうとしても、イメージが非常に難しいタイプとなります。下の図のような、同じ半径の円どうしでも、『予習シリーズ算数6年上』のP.129「発展例題1」のような半径の長さが異なる場合でも、共通するのは「同じ長さの弧の部分」に着目することです。そこで、下の図のようにそれぞれの円周上に記号やアルファベットを記しておくと、同じ長さの弧の部分をより明確にとらえることができます。

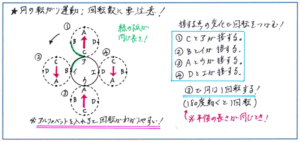
　回転数を求める問題では、『予習シリーズ』P.130～131に記載されている、「回転数＝中心が動いた長さ÷円周」の式でも求めることができますが、弧の長さから式を立てる解法を身につけておくと、初見の問題への対応力が大きくアップしますので、じっくりと解法の理解を進めておきましょう。

【第4位　立体の斜め切断：基本の成り立ちを理解して、応用パターンに対応しましょう！】

　立体の切断の中で、円柱や角柱を斜めに切断する問題では、体積が「底面積×高さの平均」で求められること、そして四角柱において「向かい合う辺の長さの和が等しいこと」という基本の成り立ちをまずはしっかり覚え込みましょう。

　この基本の成り立ちを使って解く問題として、下のような直方体の容器に水を入れて傾けるタイプの問題が出されることが多くあります。辺の長さを求める場合には、上記後者の「向かい合う辺の長さが等しいこと」を使い、そして水の体積がわかっているうえで、容器の底面積を求める場合には、高さの平均を求めることで、「体積÷高さの平均」の式でスムーズに正解を得ることができます。

　体積が「底面積×高さの平均」で求められる理由については、『予習シリーズ』でも解説されている通り、切断された同じ立体を上下逆さまにして重ねて、大きな柱体をつくれば、その体積が求める立体の体積の2倍となることから、「高さの平均」を使うことができます。実際のテストで、この理由を記述させるケースはほとんどありませんが、式の成り立ちを正確に理解しておくことは、解法の覚え込みをより強固なものにしますので、しっかりおさえておきましょう。

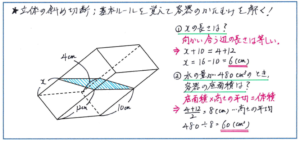
　今回ご紹介したタイプの問題は、テストの前半か中盤で出され、ここで正解できるかどうかがテスト全体の点数に大きく影響してきます。複雑な計算が発生しないタイプの問題ですので、解法をしっかり覚え込んで、確実に得点できるようにしておきましょう。

【第5位　わり切れる回数：素因数分解を使う解法の流れを確実に使いこなせていますか？】

　「数と規則性」の単元からは、約数・倍数の問題、既約分数をはじめとした分数・小数の問題と幅広い問題が出題対象になります。特に注意すべきは「素因数分解」を使った解き方をしっかりと覚え込むことにあります。

　例えば、約数の個数を求める問題では、約数を書き出すのではなく、素因数分解をした結果から計算で求める方法がスピーディーかつ正確に解き進めるために必須となります。6年生のテストともなると、約数の個数を求める問題で、その数が普段あまり接したことのないような値や、大きな数になることがあります。そうした場合に書き出しを使っていては多大な時間を要してしまいます。時間をできる限り短縮するためにも、「素因数分解→（素因数の数＋1）のかけ合わせ」、の流れがすぐに出てくるようにしておきましょう。

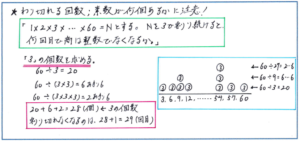
　そして解法を確認しておいて頂きたいのが「わり切れる回数」の問題です。上記の約数の個数を求める問題のように、書き出しという地道な解法が有効に使えないタイプの問題で、解法を確実に覚えていなければ、得点のチャンスが大きく減ってしまいます。下に紹介しました「1×2×3×…×60と、1から30までの整数を順にかけた積をNとしたとき、Nを3で割り続けると、何回目で商が整数でなくなりますか」といった問題。Nを素因数分解したときに、「3」を何個かけ合わせているか、つまり「3」の個数が何個あるかを調べるという流れを反復連習しておいてください。

　今回の組分けテストでは、図形の問題で手作業を多く要する問題が出される可能性が高く、テスト全体の時間配分を強く意識しなければなりません。その中で「数と規則性」の単元からの問題では、できる限り解答時間を短縮しておきたいところです。もちろん解法が浮かばない場合は書き出しの作業を進めればよいのですが、素因数分解などの強力ツールを使って、スピーディーに解答を進める対策を、しっかりと重ねておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。