メールマガジン宝箱 Mail magazine

　今回の組分けテストでは、「速さ」に関する問題での得点が偏差値アップのポイントとなります。「折り返しの旅人算」や「3人以上の旅人算」といった、旅人算の基本的な考え方を踏まえた単元が得点差を生む問題となり、また平面図形と速さを複合させた難問「点の移動」も出題範囲に含まれます。これら「速さに関する問題」、そして「数列と数表」に共通して、自分で図や表をかいて問題内容を整理する力が求められます。

　問題のどのポイントに着目して図をかけばよいのか、その図からどのように式を立てればよいのか、しっかり解法の流れを習得して、前期の締めくくりとなる組分けでクラスアップを達成したいところです。そこで、第4回組分けテストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの算数予想問題と組み合わせれば、組分けテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　2人の間のきょりのグラフ：線分図やそれぞれの動きのグラフを活用できていますか？】

　今回の組分けテストでは「速さ」に関する問題が多く出題されます。「点の移動」も速さの要素を多く含みますので、速さの解法が確実に身についているかどうか、しっかり確かめておく必要があります。

　その中でも「いろいろな旅人算」に含まれる「2人の間のきょりのグラフ」は、テスト後半に出される難問となるケースが多く、高得点を目指すためには何としてもとっておきたい単元です。このタイプの問題の難しさは、問題で提示されるグラフを見ただけでは動きが把握しづらい点にあります。ひとつのグラフで示される直線が複数になっても（複数の動きをそれぞれ表すグラフが提示されても）、一人の動きを表すグラフが1本であれば、動きはイメージがしやすくなります。

　また往復運動が含まれても、グラフの向きに気をつければ、動きの様子を把握して、グラフが交わる点が、「2人が出会う」または「1人が1人を追い越す」地点を表すことをつかむことは、大きな負担なく進められるでしょう。

　それが「1本のグラフで2人の間のきょりを表す」と変わっただけで、途端にグラフ読み取りの難度が大きくアップしてしまいます。ポイントは動きのイメージを的確につかむことにあります。そのためには、提示されたグラフをもとに、2人の動きを表す「線分図」や、2人それぞれの「グラフ」を自分でかく作業が有効であり、必須となります。

　まず大前提となるのが、『予習シリーズ5年上』の185ページの上部に示された、「グラフの傾きと2人の距離の関係」です。右下がりのグラフが2人が近づくこと、右上がりのグラフが2人が遠ざかること、そしてグラフが横軸に接する（きょりが0になる）ときには2人が同じ地点にいる、といった3点を踏まえておけば、2人の動きとグラフの形状の変化の基本形はおさえられます。あとはグラフが曲がる（傾きが変わる）地点の様子を線分図に表すか、2人それぞれの全体の動きをグラフに示せば、一気にイメージがつかめるようになります。

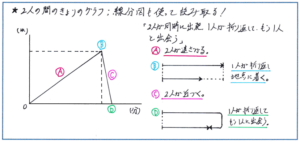
　このタイプの問題で示されるグラフは一見すると複雑な構成になっているものが多いです。それでも2人それぞれの動きが複雑になるケースは少ないので、2人の動きさえイメージできれば、解答方針は立てやすくなり、得点のチャンスが大きく広がります。グラフから動きのイメージをつかむ練習を重ねておきましょう。

【第2位　旅人算：頻出の出題パターンの解法を図を使って把握できていますか？】

　今回の組分けの重要単元である「旅人算」では、2人が向かい合って出会う、1人がもう1人を追いかけるといった基本パターンはもちろん、そこからレベルアップした応用問題で正解することが得点アップのために不可欠となります。特に注意すべきは、「折り返しの旅人算」と「3人以上の旅人算」です。

　「折り返しの旅人算」は実際の入試問題、6年になってからの模試でも頻出の問題で、いかに速く正確に解答を得るかがテスト全体の点数アップのポイントとなる単元です。気をつけておきたいのが「2回目に出会うのは何分後ですか」といった、複数回出会うケースです。ここで2回目に出会うまでに2人が進んだ距離の合計が最初の距離の3倍、初めに出会うまでに進んだ距離の合計の2倍になることをスムーズに引き出す必要があります。確実に距離の関係を理解できていれば問題ありませんが、少しでも曖昧な場合は、線分図をかいて整理しましょう。

　この「折り返しの旅人算」の考え方は、「点の移動」の問題で、図形の辺上を2点が向かい合って進むタイプの問題でも使いますので、徹底的に理解を固めておいてください。

　「3人以上の旅人算」では、2人が同じ方向に進み、もう1人が向かい合って進む際に、2人が先に出会った時点でもう1人がそれより後ろにいるという内容が頻出です。このタイプの問題では、出題のパターンがはっきりと決まっていますので、解法の流れをしっかりつかんでおけば、得点源にすることができます。

　線分図をかいて、先に出会う1人と遅れた1人の進んだ「距離の差」が、その後に出会う1人との「距離の和」になるという、同じ距離を異なる2つの式で表せることがつかめれば、一気に正解まで進めることができます。

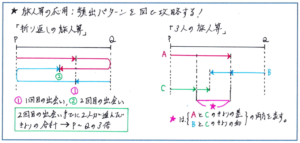
　ご紹介した2つパターンに共通してポイントになるのは、線分図で問題内容を整理することです。演習を通して慣れてくれば問題を見た瞬間に解答方針が立てられるようにはなりますが、「折り返しの旅人算」であれば距離を何倍するか、「3人以上の旅人算」ではどの部分の距離に注目すればよいのか、とった細かな点でミスが起こりがちなのが2つのパターンの特徴です。図は丁寧にかき過ぎる必要はありませんので、どのポイントに気をつければよいかを確かめながら図をかく練習を重ねてください。

【第3位　点の移動：「面積の変化」を図をかいて把握する解法の流れを身につけられていますか？】

　点の移動の問題は平面図形と速さという中学受験の最重要単元2つの要素をあわせ持つものであり、そこにグラフまでも組み合わさることが多い点で、出題者側からすれば、受験生の様々な面での理解度を一気に確かめることができるために、入試問題でも頻出となっています。

　平面図形という面では、点の移動によってつくられる図形が複雑になるケースは少なく、図形の基本性質をおさえておくことが必須です。ただし、その図形の形状が変化する様子を的確に把握するための視点の切り替え、同じ長さに着目する力が求められます。

　例えば下の図のような、長方形の向かい合う辺上を、2つの点が「異なる速さ」で移動する問題で、2点と長方形の2つの頂点でできる四角形が、「はじめて長方形」になる時間を求める場合、図形のどの部分に注目すればよいでしょうか。

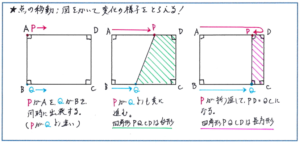
　このタイプの問題では、2点のうちの1点が「折り返してからの動き」になる点に着目して、【第2位】でご紹介した「折り返しの旅人算」の考え方を使うことになります。ここに、「点の移動」で、速さの重要単元の考え方が必須となる理由があるのです。複数の単元が混在する重要単元ですので、平面図形、速さ、グラフの基本要素の理解をしっかり確かめながら演習を進めて、必要があればそれぞれの単元をしっかり復習しておくようにしましょう。

【第4位　角速度の利用：円の中の三角形の形の変化を図をかいて理解できていますか？】

　角速度の基本的な問題では、「点が円を一周する時間」が問題で与えられ、そこから2点と円周上の別の1点でできる三角形が直角三角形になる時間を求めさせるパターンが多くあります。
この場合には、特に下の（図1）のような動く2点を結ぶ線が円の直径になるまでの時間、つまり2点が動いた角度の和が180度になるまでの時間が当てはまることに注意しておきましょう。

　そこから難度が上がった以下のような問題には、どのように対応すればよいでしょう。
「中心をOとする円周60cmの円があります。点P、Qは円周上の点Aを出発し、どちらも右回りに点Pが1周するまで動きます。点Pの速さが毎秒5cm、点Qの速さが毎秒3cmであるとき、三角形APQがはじめて、AP＝AQの二等辺三角形になるのは出発してから何秒後ですか」

　まず三角形APQがAP＝AQの二等辺三角形になるのは、どのような状態なのか、図をかいて確かめておきましょう。解答方針を立てるうえで図は不可欠ですので、丁寧になり過ぎる必要はありませんので、AP＝AQとなるように、下の（図2）のような図を完成させましょう。これで求める図形の概要はつかめました。

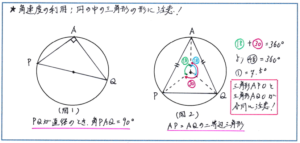
　そこで角速度の出番となりますが、この問題では紛らわしいことに、点が円周上を進む速さが与えられています。この通常の速さでは角度の問題に対応することができませんので、自分で角速度を求める必要があります。通常の速度と角速度をしっかり区別するように気を付けましょう。

　点Pは 60÷5＝12(秒) で円周上を1周しますから、点Pの角速度は 360÷12＝30(度/秒) となります。同じように、点Qは 60÷3＝20(秒)で円周上を1周しますので、角速度は360÷20＝18(度/秒) と求められます。

　ここで、求める時間をマル1秒後とします。この求める対象をマルやシカクを使って式にする解き方は今後の算数では様々な場面で使いますので、覚えておきましょう。上の図のように、角AOP＝30×マル1＝マル30度、角AOQ＝18×マル1＝マル18度と表すことができます。三角形APOと三角形AQOは合同な二等辺三角形になりますので、角AOP＝角AOQ＝マル18度となります。すると、マル18度＋マル30度＝360度であることがわかりますので、マル48＝360から、マル1＝7.5となり、求める時間は7.5秒後となります。

　このように角速度を使って考えることによって、円周上の点の移動に関する問題は解答方針が立てやすくなります。ぜひ角速度の解法を身につけておきましょう。

【第5位　数表の問題：平方数の位置、数字が増える向きに注意しながら解き進められていますか？】

　規則性の問題の中で、表の中に数字が並ぶ「数表」タイプの問題を解く際には、数字が横並びになる「数列」タイプの問題とは違った注意点があります。

　まずは表に書き込まれた数字の位置と数の性質の関係を的確につかむことが重要です。特に、表のどちらか（上下左右）の端に「平方数（同じ数のかけ合わせ）」が示されることが多いので、この平方数をヒントとすることを徹底できるように、表を見る目を鍛えておきましょう。

　例えば下の数表では、表の「1段目の奇数列目」に列の数字の平方数が、「偶数段目の1列目」に、段の数字の平方数が並んでいます。すぐに平方数が見つけられるように、目印として平方数に○を付けておくことも有効です。

　次に注意すべきは「数字が増える向き」です。数列タイプの問題はでは考える必要がないことですが、この数字の向きを間違えてしまうと、規則性をせっかく見つけ出しても正解に行き着くことができません。例えば下の数表では、数字の増える向きが、奇数段目では左から右に大きく、偶数段目では右から左に大きくと逆になります。正確に向きを把握するために、矢印を表にかき込んでイメージを視覚的にも固められるようにしてもよいでしょう。

　これらのポイントをおさえた上で、かき込みをフル活用して、数の並びの規則性を確実につかみとりましょう。例えば下の数表で「32が何段目の何列目の数か」を答える際には、まず32に近い平方数として、6×6＝36が6段目の1列目にあることに着目します。次に数字の増える向きが偶数段目では右から左に大きくなりますので、6段目は36から始まって、36、35、34、33、32と数が減って行きますので、求める答えは、「6段目の5列目」となります。最終的な答えに行き着いた際には、段や列を取り違える（5段目の6列目としてしまう）といったミスがないように注意しましょう。

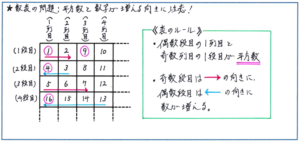
　規則性の問題では、数を書き出せば正解に行き着くことも多くあり、今回の問題でも32までであれば書き出すことも十分に可能ですが、これが600など大きな数になった際には、とても時間内に対応することができなくなります。規則を見つけ出して計算で解答を進める習慣を身につけておくようにしましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。