メールマガジン宝箱 Mail magazine

　今回の5年生夏期講習マンスリーテストの最大のポイントは、中学受験算数の最重要単元「比と割合」でどれだけ得点を重ねられるかにあります。「比と割合」の学習から、中学受験の算数は新たなステージへと進み、問題の難度もアップすることになります。今後の算数において、文章題、図形問題に関わらず、あらゆる単元で利用することになるのが「比と割合」です。

　今回のマンスリー対策を通して、まずは「比と割合」の基本的な考え方、食塩水の濃度、売買損益といった文章題、そして図形問題での比の使い方を確実におさえて、後期から本格化する比の演習に備えておきたいところです。そこで「比と割合」を中心に、夏期講習マンスリーテストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの算数予想問題と組み合わせれば、マンスリーテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　比と割合：問題文から比と割合の関係を正確に表すことができていますか？】

　夏期講習で演習した「比と割合」についてはマンスリーテストでも多くのパターンの問題が出される可能性が高いです。対策に少し時間をかかっても、比と割合の基本について理解が曖昧にならないように、徹底的に足場固めをしておく必要があります。

　まずは問題文を読んで、正確に式を立て、そこから逆比や連比をスムーズに使いこなせるようになることを目指しましょう。例えば次のような問題では、どのように比を使えばよいでしょうか。
「空の水そうにコップP、Qの2つを使って水を入れたところ、コップP 11杯とコップQ 6杯でちょうど満水になり、水そうを空にしてから再びコップP、Qの2つを使って水を入れたところ、コップP 8杯とコップQ 12杯でちょうど満水になりました。この水そうを空にしてからコップPだけで水を入れると、何杯でちょうど満水になりますか」

　問題を見てすぐに比を使えるかどうか判断する前に、まずは問題文の内容を式にしてみましょう。水そうを満水にするためのコップの使い方について、2つのパターンが表されていますので、それぞれを式にして等号で結ぶと、「P×11＋Q×6＝P×8＋Q×12」となります。ここでPとQの関係を把握するために、両辺からQ×6とP×8を引いて式を整理すると、「P×3＝Q×6」となります。

　ここから、いよいよ比の出番です。「P×3＝Q×6」から逆比の考え方で、P：Q＝1/3：1/6＝2：1となり、P＝マル2、Q＝マル1とすると、水そうを満水にするのに必要な水の量が、マル2×11＋マル1×6＝マル28となることから、コップPだけで水を入れると、マル28÷マル2＝14より、14杯でちょうど満水になると求めることができます。

　これからの算数の演習では比と割合の考え方を使わないケースはほとんどないといっても過言ではありません。今回のマンスリーの範囲となる単元で習うひとつひとつの考え方、解き方は受験算数の大事な基盤となりますので、基本でもれがないように、しっかり見直しをしておきましょう。

【第2位　食塩水の濃度：問題内容に合わせて面積図をフル活用できていますか？】

　「比と割合」の単元の中でも食塩水の濃度の問題は、入試問題はもちろん、これからのテストや公開模試で頻出度が非常に高い重要単元です。特に食塩水を混ぜ合わせる問題は、何度も混ぜ合わせを行う「やりとり」の問題のようなタイプになると複雑さが一気に増し、難度が上がってきます。

　そうした難問を含め、混ぜ合わせの問題に対応するには「面積図」が不可欠ですので、まずは今回のマンスリー対策を通して、基本的な混ぜ合わせの問題で正確にスムーズに面積図がかけるように練習を重ねておきましょう。　

　例えば次のような問題を見て、すぐに面積図がかけるでしょうか。
「18%の食塩水（ア）gと、10.5%の食塩水（イ）gを混ぜると、15%の食塩水が500gできます。（ア）と（イ）にあてはまる数を答えなさい」

　この問題では、2つの食塩水について、濃度、食塩水の量、食塩の量のうちわかっているものが濃度のみですので、計算で解くのは困難になります。そこで面積図を利用すると、複雑な計算をすることなしに正解まで行き着くことができるのです。注意すべきは、面積図の斜線部分の面積を出してしまうのではなく、「同じ面積の長方形のたての長さと横の長さは逆比の関係にある」という考え方を使う点です。面積を出すよりも圧倒的に速く正確に解くことができます。

　また、図の右側にあるような、「食塩を加える」「水を加える」といったケースでも面積図を使って解くことができますので、それぞれのかき方も合わせて覚えておきましょう。

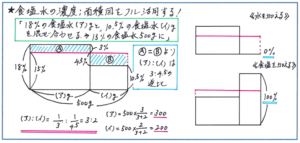
　今回のテスト範囲では、「平均算」でも面積図を使って解くことができる問題が多数出てきます。そして今後、速さを含め、比を使った問題ではどの単元でも有効な武器をなるのが面積図です。今回の対策を通して正確にスムーズに面積図をかけるようにしておきましょう。

【第3位　立体図形と比：3.14を使わずに比で解き進める方法を使いこなせていますか？】

　立体図形では、直方体を扱う問題にしても円柱を扱う問題にしても、計算が複雑になってしまうケースが多くありますが、それらの問題でも比を使うことで解き方が断然楽になります。

　ここでは、2つの円柱の容器に入った水をやりとりして、水の深さを等しくするタイプの問題を例に、比の使い方を考えてみましょう。下の図のような「底面が半径12cmの円である円柱の容器Aと、底面が半径8cmの円である円柱の容器Bがあり、容器Aには深さ12cm、容器Bには深さ25cmまで水が入っています。容器Bから容器Aにこぼれないように水を移して、2つの容器の水の深さが同じになるようにした時に、水の深さは何cmになりますか」といった問題です。

　まずこの問題のような水の深さを同じにする問題を解く際には「水の体積の和を、底面積の和で割る」という考え方が大前提になることはしっかりおさえておいてください。ここで計算なのですが、底面の円の面積を求める際に3.14が入り、さらに容器Bの水の深さが21cmという大きな値ですので、計算が複雑になることは避けられません。

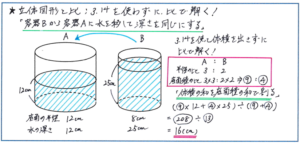
　そこで、比を使う解き方で進めてみましょう。容器Aと容器Bの底面の半径の長さの比は、12：8＝3：2ですので、底面積の比は3×3：2×2＝9：4となります。ここで容器Aの底面積をマル9、容器Bの底面積をマル4と置いて、そのまま体積の計算を進めます。容器Aの水の体積は、マル9×12＝マル108、容器Bの水の体積は、マル4×25＝マル100となります。

　最後に、先ほど触れました「水の体積の和を、底面積の和で割る」の考え方から、水の深さを求めて行きます。水の体積の和が、マル108＋マル100＝マル208で、底面積の和がマル9＋マル4＝マル13ですので、マル208÷マル13＝16より、水の深さは16cmと求められます。

　比はその使い方に慣れるまでは扱いづらく感じるかもしれませんが、使いこなせるようになると、単元を問わす利用できるうえに、計算量を大きく減らせるという大きなメリットがあります。すぐに計算で解くのではなく、まず比が使えないかどうかを考える習慣を身につけるようにしましょう。ただし、テストでは時間が限られますので、比の使い方が思い浮かばなかった場合は、そのまま計算で進めるようにしてください。

【第4位　売買損益：割引き・割増しが2回以上ある時の式を正確に立てられていますか？】

　「比と割合」の単元の中で【第2位】の「食塩水の濃度」と同様に注意しておきたいのが、「売買損益」の問題です。まずは、定価、利益といった言葉の意味を確実に把握して、正確な式を立てることが基本となります。

　そのうえで注意しておきたいのが、価格の設定が2段階になる問題です。例えば、「原価の3割の利益を見込んで定価をつけましたが、売れなかったので定価の20%引きを売値とした場合、何%の利益が出ますか」といった問題であれば、原価（仕入れ値）を1として、定価を1.3に、20%引き（80%）の価格が売値となるので、「1.3×0.8＝1.04」の式から、利益は「1.04－1＝0.04」より4%と求められます。このかけ算を連ねる式は基本ですので、式の立て方についての理解が少しでも曖昧な場合は急ぎデイリーサピックスで復習をしてください。

　これが「原価の2割増しで定価をつけましたが、売れなかったので420円値引きして売ったところ、原価の6%の利益が出ました。原価はいくらですか」といった問題になった場合にも、正確に式を立てられるでしょうか。

　売買損益の問題の難しさのひとつは、言葉の使い方が少し変わっただけで解きづらさが一気に増してしまうことにあります。言葉の基本的な意味に立ち返って、やはり原価を1として式を考えると、定価は1.2で売値は原価に利益の6%を加えた1.06となります。この1.2と1.06の差が値引き分の420円に当たりますので、原価をマル1とすると、マル1.2－マル1.06＝マル0.14が420円となることから、マル1＝420÷0.14＝3000より、求める原価は3000円となります。

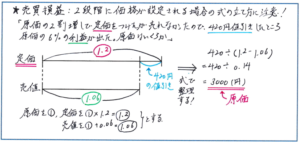
　売買損益の問題では価格の変化を正確に把握するために、まずは言葉の意味を正しくおさえておくことが必須ですが、理解をより確実にするためには、上のような線分図で整理することも有効です。慣れれば線分図なしでも解き進められますが、言葉の意味が自分の中にしっかり浸透するまでは、線分図で整理するという作業が効果的です。

【第5位　点の移動：面積の変化を「場面分け」して把握できていますか？】

　今回のマンスリーでは比の問題以外にも、夏期講習で演習した重要単元がテスト範囲になります。その中でも平面図形の「点の移動」の問題は、点の位置を場合分けして考える力が試されるため、テストで頻出となります。

　問題としては、動く点によってできる図形の面積の変化が出題対象となることが多いです。時にその変化がグラフによって表されることもありますが、変化の状況をどれだけ正確に把握できるかが得点できるかどうかの分かれ道になります。

　面積の変化を、頭の中だけでイメージしようとすると、段階的に増え方、減り方が変わる面積の変化を正確に把握できなくなり、時間がかかるばかりで得点にならないといった事態が起こりがちです。特に速さの異なる2点の動きとなると、動く点が1つだけの場合よりも、動きのイメージが数段にしづらくなります。2点の動きによってできる図形の面積の変化を正確に把握するためには、自分で図をかいて、点の位置によって「場面分け」をしてそれぞれの面積を求める必要があります。

　例えば下の図で、長方形ＡＢＣＤの辺ＡＤ上を点Ｐが頂点Ａを、辺ＢＣ上を点Ｑが頂点Ｂを同時に出発して、辺上を往復する際の四角形ＡＢＱＰの面積の変化を考えるとします。点Ｐが点Ｑより速く動くとした場合、まず点Ｐが頂点Ｄに着く時点（下の図1）、次に点Ｑが頂点Ｃに着く時点（下の図2）、点Ｐが頂点Ａに着く時点（下の図3）、そして点Ｑが頂点Ｂに着く時点（下の図4）として場合分けします。

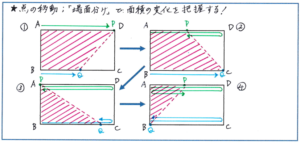
　注意すべきは、これはあくまで基本形で、例えば点Ｐと点Ｑの速さの差が大きい場合には、点Ｐが往復して点Ａに戻りつく方が、点Ｑが点Ｃに着くよりも早いケースがあります。その場合も、各点が頂点に着く時間が算出できれば、基本形を変更させて簡単に状況が把握できます。

　そして気をつけておきたいのが、点が動き始めてからの時間と面積の関係がグラフとなって表された場合です。グラフが並び表されると、より問題の内容が複雑になる印象がありますが、グラフによって点の速さや辺の長さといった、面積の変化を把握するうえで必要なデータが得られるという大きなメリットがありますので、グラフの変化する点に注目して、グラフから与えられる数値をフル活用する練習をしっかり重ねておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。