メールマガジン宝箱 Mail magazine

　今回の5年生第5回組分けテストは、これまでに習った内容のすべてがテスト範囲となります。その中でも特に、夏期講習で学習した「比の基本」「相似」「面積比」といった比に関する単元には注意が必要です。

　中学受験算数の最重要単元「比」については、後期から本格的に取り組むことになりますが、そこで中学受験の算数は新たなステージへとレベルアップします。まずは夏期講習で習った「比」の基本範囲を徹底的に理解しておきましょう。

　今回の組分けテスト対策を通して、比に関する基本範囲をマスターして、後期からの学習へ向けて足場固めを万全にしておきたいところです。そこで「比」の単元をはじめ、第5回組分けテストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの算数予想問題と組み合わせれば、組分けテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　比の基本：「比の1あたりの量」の求め方は理解できていますか？】

　まずは比の基本的な文章題について、問題文から的確に比の関係を作り、それをもとに「比の1あたりの量」を求める流れを確実に理解することが必須となります。

　例えば、「A君はミカン8個とリンゴ5個を買い、B君はミカン3個とリンゴ7個を買ったところ、2人の代金は等しくなりました。また、C君はミカン5個とリンゴ4個を買ったところ代金は900円になりました。このときA君の代金はいくらですか」という問題で、比を正しく使えるでしょうか。

　まず、問題文から比の関係を作ります。ミカンとリンゴそれぞれ1個の値段を「ミ」、「リ」とすると、A君とB君の買い方から、「ミ×8＋リ×5＝ミ×3＋リ×7」という式を立てることができます。この式の両辺から、「ミ×3」と「リ×5」を引くと「ミ×5＝リ×2」となります。この式の整理の方法は今後も多く使いますので、早めにマスターしておきましょう。

　ここで逆比を利用することがポイントとなります。「ミ×5＝リ×2」より、ミ：リ＝1/5：1/2＝2：5から、ミカン1個とリンゴ1個の値段の比が2：5と求められます。

　次に「比の1あたりの量」を求め、ミカンとリンゴの1個あたりの値段を求めます。C君の買い方から「比の1あたりの量」は　900÷(2×5＋5×4)＝30(円)となり、ミカン1個は 30×2＝60(円)、リンゴ1個の値段は 30×5＝150(円)と求められます。これより、A君の代金を、60×8＋150×5＝1230(円) と求めることができます。

　この解き方の中で、特に注意しておきたいのが、逆比の求め方です。「ミ×5＝リ×2」から「ミ：リ」の比を求める際に、機械的に5と2を逆にする解法のみを覚えてしまうと、「a×5＝b×2＝c×3」といった3つの関係を求める際に、解き進められなくなってしまいます。分数を使う解法を定着させておけば、「a：b：c＝1/5：1/2：1/3＝6：15：10」とスムーズに求めることができます。逆比と連比の求め方は今後も何度となく使う解法ですので、確実に覚え込んでおきましょう。

【第2位　面積比の問題：面積比と辺の長さの比の関係は把握できていますか？】

　平面図形における比の問題を解く際に、「高さが等しい三角形の面積の比は、底辺の比と等しい」という、今後の平面図形で、くり返し使うことになる重要な考え方があります。この考え方を使って補助線を引き、応用問題にも対応できるようにしていきましょう。
　
　例えば下の図のような三角形の各辺を延長してできる大きな三角形と、もとの小さな三角形の面積を比べるタイプの問題の解き方をすぐに思い浮かべることはできているでしょうか。

　図を見ても、このままでは「高さの等しい三角形」を見つけることができません。そこで補助線を引いて「高さが等しい三角形」を作るという作業が必要となります。

　まず、頂点Dから頂点Cに補助線を引いてみましょう。すると「高さの等しい三角形」、三角形CABと三角形CBDができます。三角形ABCの面積を1とすると、AB：BD＝1：2より、三角形CBDの面積は 1×2＝2 となります。また、この補助線DCを引くことにより三角形DBCと三角形DCEも「高さが等しい三角形」になっています。三角形DBCの面積は2だったので BC：CE＝1：3より、三角形DCEの面積は 2×3＝6 となります。

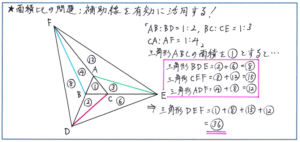
　同じように考えて、補助線EA、FBを引いて考えると、三角形EACの面積は1×3＝3、三角形EFAの面積は 3×4＝12、三角形FABの面積は 1×4＝4、三角形FBDの面積は 4×2＝8 とそれぞれ求まります。したがって、三角形DEFの面積は 1＋2＋6＋3＋12＋4＋8＝36となり、三角形DEFの面積は三角形ABCの面積の 36÷1＝36(倍)と求まります。

　この問題のように平面図形では、補助線を引くと解答方針を一気に立てることができるようになる問題が多いです。ここでポイントになるのは、補助線を引く際に、「自分の知っている形を作る」と考えて臨むことです。平面図形が苦手なお子様方にとって、補助線を引くという作業が負担に感じられないように、作業の方向性を明確にすることが大事になります。

【第3位　通過算・流水算：図をフル活用することがスピーディーに正解するポイントです！】

　範囲のない組分けテストで、入試頻出の「速さの問題」が出題されるケースは非常に多く、様々なパターンの問題が出されます。その中でも「通過算」「流水算」では、問題内容を正確に図で整理して式を立てられるかどうかが、得点を重ねるためのポイントになります。

　通過算では、速さ、長さの異なる列車どうしが追いつき追い越される場面、すれ違う場面を図にすることで、「列車の長さの和を速さの和（または差）で割って時間を求める」という鉄則を視覚的にイメージできるようにしておく必要があります。

　その際に『予習シリーズ』の図でも示されている通り、例えば列車が別の列車を追い起こす場合には、「追い越す列車の先頭を○、最後尾を●、追い越される列車の最後尾を○、先頭を●として、○が一致する時点から●が一致する時点までの時間を求める」とすることで、列車が追い越す際に進む距離を正確に理解することができます。すれ違う場合には、両方の列車の先頭を○、最後尾を●とすれば同じように長さをとらえやすくなります。

　ほんの一手間ですが、この作業に慣れておくと、解答方針がはっきりと見えてきますので、図をかかない場合よりも時間も短縮できて、正答率も上がる効果があります。それでも図のかく時間をかけ過ぎないのうに、列車や鉄橋をかく際には、あくまでシンプルに、単純な四角で表して、列車の窓や車輪までかき込むことは避けましょう。時間がかかる上に、図が複雑になって、より見えづらくなってしまいます。

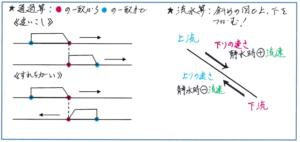
　流水算では、船の「上り」「下り」の動きを把握しやすくするために、「斜めの線分図」を利用する方法が効果的です。線分図を斜めにかき、川の上流と下流の位置を示すことで、上りの速さと下りの速さの関係を視覚的にとらえることができるようになるのです。

　こうした図のかき方を基本的な問題を通して練習しておくことが、上り・下りの船の動きを正確に把握する力の養成につながります。流水算は今後、船の出会い算や、船が故障して流される、といった様々な出題パターンが出され、さらにそれらのパターンをグラフとの関連で解き進めることになり、一気に難化して行きます。そうした難問に対応するためにも、有効な図のかき方を身につけておきましょう。

【第4位　水深の変化：立体を真正面から見た平面で考える習慣が身についていますか？】

　立体図形の「水深の変化」の問題では、水を入れる水そうの形が「仕切りが入った形」や「腰かけの浴そうの形」であるケースが多く出題されますが、そうした問題に対した際に気をつけておきたいのが、見た目の複雑さを意識するあまりに、問題を解く手が止まってしまうような事態を避けることです。

　このタイプの問題では水そうの形に合わせて、「段階を分けて解く」といった作業が必要なうえ、グラフと水そうの形の関係にも着目しなくてはならない点で、問題の難度が上がることは確かです。それでも、「水そうの形とグラフの関係を明確にするための図」を使って解き進めれば、水深変化の状況が一気にイメージしやすくなります。

　その図とは、水そうを真正面から見た「断面図」のような平面です。このタイプの問題に出てくる水そうの形は、仕切りが入ったり、段差がついたりと複雑になっても、「奥行きの長さ」が一定であるケースがほとんどです。そこで、立体の体積を一定の奥行きの長さで割って求められる平面で考えることができるのです。

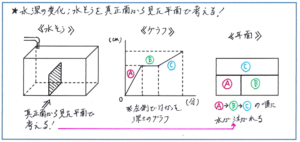
　上の図のように、平面を分けることで、平面の中で起こる変化を水深の変化につなげて考えることができます。さらにはグラフの変化と、分けられた平面の関係を把握することで、水深の変化とグラフの関係も正確につかむことができるようになります。

　このタイプの「水深の変化」の問題は組分けテストでも後半の応用問題として出されるケースが多く、問題によっては、立体の成り立ちだけでも理解すれば解ける問題で正解できる小問が(1)(2)で出されることが多く、そうした小問を正解することで、テスト全体の得点を大きくアップさせることができます。

　そのためには、立体を平面に変換させて考えるという、立体の成り立ちを理解するための重要なステップを経て、式を立てる習慣をしっかりと身につけておきましょう。

【第5位　規則性の問題：複数の数列が出される問題に正確に対応できていますか？】

　規則性の問題では、数列の問題、特に複数の数列が出される問題に注意が必要です。例えば、以下のような2つの数列に「共通して並ぶ整数」を考えるような問題で、着目すべきポイントはすぐに思い浮かぶでしょうか。
数列A　3、7、11、15、…
数列B　2、5、8、11、…

　数列Aは3からはじまり、4ずつ数が増える等差数列で、数列Bは2からはじまり、3ずつ数が増える等差数列であることはすぐに気づくでしょう。この2つの数列に共通して並ぶ整数について、「最初に共通する整数の11」に着目すれば、そこから後は4と3の最小公倍数である12ごとに数が増え、11、23、35、…と共通する整数が並ぶことがわかります。

　これは数の性質の問題で、あまりが共通でもなく、足りない数が共通でもない整数の求め方に通じるものですので、解答のイメージが立てやすいでしょう。

　その他では、分数の数列で、分子と分母が異なる規則で数が変化する問題についての対策も必要となります。上のような、「1/301、3/298、5/295、7/292、9/289、…」といった分数の数列で、「約分すると1になる分数がならぶのは、左から数えて何番目ですか」といった問題で、解答方針がすぐに立てられるでしょうか。

　この分数の数列では、分子は「1からはじまり、2ずつ数が増える等差数列」で、分母は「301からはじまり、3ずつ数が減る等差数列」となります。約分すると1になる分数は「分子＝分母」ですので、1番目の分数は分子が分母より(301－1＝)300小さく、2番目以降、分子と分母の差が(2＋3＝)5ずつ縮まりますので、300÷5＝60より、求める分数がならぶのは、(60＋1＝)61番目となります。速さの旅人算の考え方につながる解法です。

　まずは基本的な等差数列の考え方、和の公式の理解を確認して、数の並び方をスピーディーにつかむ練習を重ねておきましょう。その練習によって複数の数列が出される問題でも、着目するポイントが一気につかみやすくなります。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。