メールマガジン宝箱 Mail magazine

　今回の5年生10月度マンスリーテストでは、夏期講習で演習した「比と割合」を応用させた問題でどれだけ得点できるかが大きなポイントになります。特に「旅人算」では、中学受験算数の最重要単元である「速さと比」をいかに的確に使えるかを試す問題が多く出されます。今回のマンスリー対策を通して「速さと比」への対応力を培っておくことは、今後の算数対策の礎を築くことにもつながります。

　その他にも比を使った解法を使いこなして解く「仕事算」や、図をかいて解く力が求められる「図形の移動」「時計算」といった、得点差の生まれやすい単元がテスト範囲に含まれる今回のマンスリーで、何としてもクラスアップを達成したいところです。

　そこで「速さと比」をはじめ、比の使い方を中心に、10月度マンスリーテストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの算数予想問題と組み合わせれば、マンスリーテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　旅人算（速さ・距離・時間の関係）：最重要ポイント「逆比」を使いこなせていますか？】

　夏期講習で「比」を演習したことで、5年生の算数はステージが何段もアップしたことになります。5年後期からは、夏期で基本内容を演習した比を使った様々なタイプの問題の演習が本格化して行きますが、まず今回の10月度マンスリーでは「旅人算」の演習を通して、比をフル活用して解く速さの問題に臨みます。

　旅人算の基本はすでに演習済みですが、比の要素が入ることによって問題の複雑さは高まります。難度が大きく増すのは確かですが、比を使うことで、式が簡略化され、簡単な計算で解くことができるメリットも生まれます。そのメリットを最大限生かすために不可欠なのが「逆比」の考え方です。「同じ距離を進む場合には、速さの比と時間の比は逆比の関係」という大前提を使いこなせるかどうかが、今回のマンスリーで高得点をとるための必須条件となります。

　この逆比を使えれば、例えば「太郎君は8時55分に家を出発しました。太郎君の忘れ物に気づいた兄が9時5分に家を出発し、太郎君を追いかけました。太郎君の速さは分速60m、兄の速さは分速80mのとき、兄が太郎君に追いつくのは何時何分ですか」といった追いつき型の旅人算の基本パターンの問題も、よりスムーズに解くことができるようになるのです。

　比を使わずに、これまで使っていた旅人算の基本的解法で解くと、時間の差の10分を太郎君の速さにかけて2人の距離の差を求めてから、それを速さの差で割る、といったかたちで作業が多くなり、ミスが起こる可能性も高くなってしまいます。

　ここで逆比を使うと作業を一気に減らすことができます。家から兄が太郎君に追いついた地点までの距離を、太郎君と兄が進む時間の比は、2人の速さの比の逆比となるため、1/60：1/80＝4：3となります。この比の差1が10分にあたりますので、兄が出発してから10×3＝30（分後）に太郎君に追いつくことになり、9時5分＋30分＝9時35分と、スムーズに正解に行き着くことができるのです。

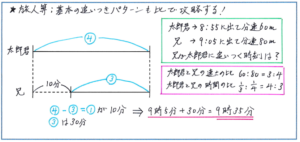
　ここで時間の差と比の差の関係をより把握しやすくするためにも、線分図をかくことをおすすめします。線分の長さの違いで視覚的に「差」が把握しやすくなります。

　比の要素が加わることで問題の難度が上がることが強調されてしまいがちですが、比を使った解法、特に逆比を使いこなすことができれば、むしろ計算の難度は下がり、解答速度・正答率ともに大きくアップするという大きなメリットが生まれます。これは速さに限ったことではなく、図形でも食塩水の濃度などの文章題でも、比がテストの点数を大きくアップさせる強力な武器となることをしっかり認識しておきましょう。

【第2位　旅人算（遅刻の問題）：時間の差を正確に把握するためには線分図が有効です！】

　旅人算の中で「時間の差」を扱った問題のうち、「昨日は始業時刻の5分後に学校に着いたが、今日は2分前に着いた」といった「遅刻の問題」は今回のマンスリーで出される可能性が高く、また入試でも頻出です。このタイプの問題はマンスリーの中盤で出されることが多く、ここで得点できるかどうかが、テスト全体の得点を高く安定させられるかどうかの分かれ目になります。

　このタイプの問題は解き方を習得しさえすれば、問題を見た瞬間に式を立てられるようになりますが、慣れないうちは「遅く着く、早く着く」という状況をどのように式にすればよいか、迷ってしまいます。その迷いが生じる理由のひとつは、距離の差と違って時間の差が目に見えるものではないという点にあります。そこで時間の差を視覚化するために、慣れないうちは線分図をかくことをおすすめします。

　速さの線分図には、例えば往復運動のように、どうしても複雑になるものもありますが、この「遅刻の問題」での線分図は下のようにいたってシンプルです。時間も手間もかからずに正確さを増す効果がありますので、ぜひ試してみてください。

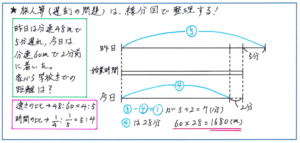
　注意しなくてはいけないのが、距離を求める場合です。時間の差を把握するためにかいた線分図では、速く着く場合の線分図は短くなります（通学にかかる時間が短いので当然のことです）。ここで速く着く場合の速さにかける時間を、学校の始業時刻までの時間としないように気をつけてください。あくまで「通学にかかった時間」に速さをかけるように注意しましょう。

【第3位　図形の移動：細かいミスを防止するために、自分で図をかいて動きを把握しましょう！】

　「図形の移動」の単元では「平行移動」「ころがす」「回転移動」の問題を扱いますが、このうち「ころがす」「回転移動」については、デイリーサピックスでかなり幅広くパターンが網羅されていますので、まずはデイリーを熟読して解法パターンを頭にしみ込ませておきましょう。

　「平行移動」も解き方はシンプルですが、移動する図形のかたちが様々ですので、変化の状況を正確に把握することが難しいケースがあります。問題によっては図形が動く時間と2つの図形が重なる部分の面積の関係を表したグラフが合わせて出てくることがあります。

　様々なかたちの出題パターンに対応するためにも、図形が重なる様子を自分でかく解法を身につけておきましょう。その際に、動かない図形の上に動く図形を何度も書き足してしまうと、問題によっては図がとても見づらくなってしまいます。少し手間はかかりますが、「重なりの段階」に分けて図をかく方がよいでしょう。ポイントは長さを正確に書きこむことです。図形の枠はもちろんフリーハンドで、見分けできる範囲であれば多少雑でも構いません。ただ、長さを表す部分については、見間違いがないように、丁寧に書くようにしましょう。

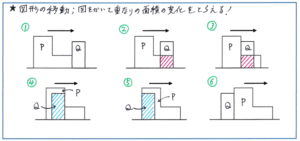
　そうして図をかいておけば、「○秒後には重なりは何平方cmですか」といった基本パターンはもちろん、重なりの部分の面積の変化がつかみやすくなり、先に触れたようなグラフ問題にも大きな負担なく対応できるようになるのです。

　もちろん図をかくためには時間が必要で、重要単元が立て続けに出てくる今回のマンスリーで、ゆっくりじっくり図をかく時間はありません。テスト前に1回でも構いませんので、自分で図をかく練習をしておいてください。シミュレーションをしておくことによって、テスト当日に落ち着いて問題に臨むことができます。

【第4位　仕事算：比の解法を活用する「共通量」の解き方を覚えられていますか？】

　仕事算の問題の中で特に気をつけておきたいのが、デイリーサピックスで「共通量」として取り上げられている問題です。仕事算の問題内容の多くが、仕事を終わらせる、注水菅や排水管を使って水そうの中の水を出し入れするパターンで、「共通量」の問題もデイリーサピックスでは仕事を終わらせるパターンの問題が紹介されていますが、実際のテストでは、買い物など、一見仕事算とは関係ないようなパターンで出されることがあります。そのような場合に、解き方に迷うことなく正確に対応する必要があります。

　例えば「商品Aを8個と商品Bを16個ちょうど買えるお金で、商品Aを5個と商品Bを25個買えることがわかりました。このお金で、商品Aと商品Bをできるだけ多く、同じ個数ずつ買うとすると、何個ずつ買うことができますか」といった問題は、どのように解き進めればよいでしょうか。

　商品Aと商品Bという単価の異なる2種類のものを2つのパターンで買う、というかたちから消去算の解き方が浮かんできますが、必要な合計代金がわかっていません。ここで比の考え方を使うのが、この「共通量」の問題です。それぞれのパターンの買い方を式にして、その式を照らし合わせて簡単にすることで、商品Aと商品Bの1個の代金の比を求める、といった流れになります。

　詳しくは下のようになりますが、ポイントはa×8＋b×16＝a×5＋b×25がわかってから、a×3＝b×9の式までを正確に進めることです。細かい計算ミスをしないように注意しましょう。

　今回取り上げた問題は、比を使うことで、わかっている数値が少なくても答えを求めることができるという、比のメリットが活用できるパターンのひとつです。仕事を終わらせる、水そうの中の水を出し入れする、といった仕事算の基本パターンをしっかりおさえたうえで、「共通量」という独特の解き方をする問題で確実に得点ができるように、解き方の流れをしっかり確認しておいてください。

【第5位　時計算：針の動きを正確に把握するための図をかけていますか？】

　速さの問題の中でも時計算は「角速度」を用いる点が特徴的ですが、基本的な考え方は旅人算と同じなので、角度の関係を正確に把握して、分数計算でミスをしないように気をつければ、正解への道筋は立てやすい単元です。

　ポイントとなるのは3点。まず長針と短針の速度の差が毎分5.5度であることを機械的に覚えないことです。長針が毎分6度、短針が毎分0.5度なので、6－0.5＝5.5（度）であるという成り立ちを忘れないようにしてください。細かすぎるように思われるかもしれませんが、6＋0.5＝6.5（度）を使う問題や、針の速度が必ずしも6度、0.5度ではない問題が出されることもあり得るのです。そうした際に5.5度をただ暗記してしまっていると解答方針が立てられなくなってしまいますので、当たり前のことではありますが、長針の角速度と短針の角速度の差が5.5度である、という大前提をいま一度確認しておいてください。

　2つ目は図をかくことの重要性です。最初にも触れました通り、時計算攻略のカギは角度の位置関係を正確に把握することにあります。長針と短針のはじめの位置関係を作図したうえで、そこに角度をかき込む、そして問題で問われている状態の図もかく、といった作業をすることで針の動きのイメージがつかみやすくなり、式をより早く立てることができるようになるのです。

　針が円周運動をするために、頭の中で動きをイメージすることが困難になります。ラフなスケッチで構いませんので、ぜひ図をかく練習をしておいてください。特に「4時と5時の間で、長針と短針の作る角が直角になるのは4時何分と何分ですか」といったタイプの問題の際に、図をかく効果が増大します。

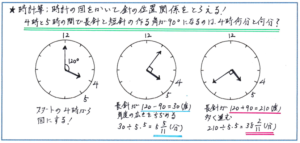
　最後に計算について、角速度の差が5.5度の時の時間を求めると、どうしても計算結果が11を分母とする分数になります。正確にわり算をしてあまりを求め、帯分数にするのですが、ぜひ計算の見直しを解答の直後に行ってみてください。というのも、11倍（×11）は筆算が非常にやりやすいため、分母が11の分数は見直しが簡単にできるメリットがあるのです。

　せっかく式を立てられても最後の計算でミスをしてしまっては、大事な得点がすり抜けて行ってしまいます。比を使った旅人算や図形の移動といった難問が出される今回のマンスリーでは、この時計算では何としても得点を重ねておきたいところですので、計算の見直しをする前提で時間配分を設定し、見直しの練習をテスト前に重ねておくとよいでしょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。