メールマガジン宝箱 Mail magazine

　今回の5年生11月度マンスリーテストでは、「相似」そして「面積比」という平面図形の中でも特に入試頻出度が高い単元が範囲に含まれます。10月マンスリーでは「比と速さ」、11月マンスリーでは「比と図形」と、立て続けに比に関する重要単元が出題されるこの時期は、まさに中学受験算数における「勝負の時」と言えます。ここでのテスト対策を通してじっくり比の理解を固めることが、今後の算数での得点力アップを実現させるために必須となります。

　その他にも速さの重要単元であり、比を使うケースが多い「流水算」も範囲となる今回のマンスリーで、何としてもクラスアップを達成したいところです。そこで、「比を使って解く問題」を中心に、11月度マンスリーテストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの算数予想問題と組み合わせれば、マンスリーテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　比と図形：向きの異なる相似な図形の対応する辺が正しく求められていますか？】

　今回のマンスリーテストのメイン単元のひとつ「相似」は、実際の入試問題においても、平面図形の中で最頻出の重要単元です。夏期講習から演習してきた「比」を図形の中で利用して解くこの相似の問題を正確に解き進められるかどうかが、今後の算数のテスト、そして入試算数で高得点をとるための必須のポイントとなります。今回のマンスリー対策を進める中で、相似の基本をしっかり固めて行きましょう。

　まず基本としておさえておくべき内容は、相似の関係にある図形の「対応する辺の長さの比」を正確に求めることです。テキストの前半に出てくる基本的なピラミッド型やクロス型の形であれば、見た瞬間にどの図形とどの図形かがわかりますが、気をつけなくてはならないのが「向きの異なる相似な図形」の場合です。

　例えば下の図のように、相似な図形が向きを変えて示された場合、どの辺が対応するかを取り違えてしまうと、相似比を正しく求められても正解に至ることができなくなってしまいます。こうした問題の場合、塾の授業でも指示されていると思われますが、「同じ角度に印をつける」ことで、対応する辺の関係を見やすくすることができます。

　対応する角度に同じ印をつけた上で、下の左の図であれば、角度の「○→●→△」の順に、向かい合う辺の長さの比が、アの図形では、「20：a：18」、イの図形であれば「40：32：b」とわかります。あとは、a＝32×20/40＝32×1/2＝16（cm）、b＝18×40/20＝12×2/1＝36（cm）と求めることができます。

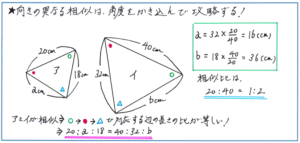
　ここでご紹介したタイプの問題は、テストの前半で出される可能性が高いので、何としても得点しておきたいところです。そして、この向きの異なる相似の図形での対応する辺の関係を正確に求められるようになっておけば、後半の大問に対応する基盤を固めることができます。見た目で判断しようとするとミスを起こしてしまいますので、慎重にかつスピーディーに対応する辺の関係を求められるように練習しておきましょう。

【第2位　比と図形：「三角形を区切る」問題では分数計算の流れを確実に身につけておきましょう！】

　今回のマンスリーにおいて、「相似」と同様に平面図形において入試頻出の重要単元であるのが「面積比」です。例えば下の図のような三角形を区切るタイプの問題は、一見複雑そうでも、解き方さえしっかり固まっていれば、いたってスムーズに解き進められるタイプの問題の典型です。

　ポイントは三角形の図の中に、与えられた比を書き込んで、比の値を取り違わないようにすることです。あとは、分数のかけ算を慎重に進めれば、中央の三角形が大きな三角形の何倍かをすぐに求めることができます。

　このタイプの問題は、分数のかけ算で解く方法を確実に覚えておけば正解できる可能性が大きく上がりますが、その計算式で解ける理由を正確におさえておけば、かけ算を使う解法がすぐに思い浮かばなくても、正解することができます。

　左の図のように、点線の補助線を入れることで、三角形ABEと三角形CBEの面積比はAE：CEとなることから、三角形ABEの面積は三角形ABCの面積のAE/AC倍、三角形AEFの面積は三角形ABEの面積のAF/AB倍、となることから、三角形AEFの面積は、三角形ABCの面積の、(AF/AB×AE/AC)倍、と求めることができます。

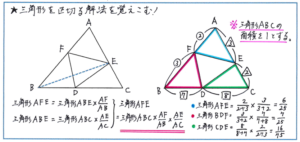
　この補助線から面積比を求めるという流れを確実におさえておけば、問題を見てすぐに分数計算の式を立てられなくても、正解へと行き着くことができます。解法の流れのイメージをしっかり固めるためにも、自分で補助線をひいて解く習慣を身につけておきましょう。

　また、比の値を間違って計算しないように、図形の中への比のかき込みを正確に速く進められるようにしましょう。特に、AF/AB倍とすべきところを、AF/BF倍としてしまう間違いは、相似の問題を解く際にも起こり得ることですので、長さの関係を正確にとらえて解き進めるように、注意して臨みましょう。

【第3位　比と図形：クロス型の相似をつくるための補助線を正確にひくことができていますか？】

　相似の問題で、【第1位】でご紹介しました基本的な内容からさらにレベルアップした問題として、長方形や平行四辺形、台形の中にある相似の関係を的確につかむ力を求める問題があります。テストの中盤以降に出てくる可能性が高く、まさに得点の分かれ道になる重要単元となります。

　特に注意しておきたいのが、与えられた線だけでは相似の関係を見つけることができないケースです。例えば下の図のように台形ABCDの中に2本の直線がひかれている問題。まず辺ABと辺CDが平行ではないので、三角形BEFと三角形CDFは相似の関係にはなりません。まずは、相似の関係を取り違えないように、図形を見る際には常に「平行線」に着目するようにしてください。

　ここでは、辺ADと辺BCが平行であることから、「あと一歩でクロス型の相似になる」と考えることが、正解への大きなステップになります。与えられた図形で相似がなければ、自分でつくってしまえばよいのです。DAとCEをそれぞれ延長させた線の交わる点をGとすれば、三角形GDFと三角形CBFが相似となります。

　さらに、三角形AGEと三角形BCEも相似になります。ここでBF：DF＝1：1であるため、DGの長さが、BCと同じく27cm、AGの長さが27－18＝9（cm）より、AE：BE＝AG：BC＝9：27＝1：3と、比を求めることができます。線を延ばして新しい三角形をつくる手間がかかりそうですが、相似の関係を一旦つくってしまえば、比や長さが次から次へとわかって行きます。この流れをぜひつかんでおいてください。

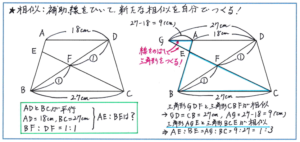
　相似の関係にある図形を自分でつくる際に注意しなくてはいけないのが、やはり「平行線」です。上記の図形であれば辺ADと辺BCのように、平行な関係さえつかめれば、相似の図形はつくりやすいです。クロス型の相似の関係を図形の中に見出す意識を固めるために、相似の基本型を頭の中に刷り込み、平行線の存在を常に意識する習慣を身につけておきましょう。

【第4位　流水算：静水時の速さ、流れの速さに比が使われた場合に対応できていますか？】

　流水算の中でも、比を使って解く問題が範囲となるのが今回のマンスリーです。静水時の速さや流れの速さが変化する際に、比の要素が入ってくるパターンがあります。

　例えば「ある船が川を28.8㎞上るのに16時間かかりました。同じ川を、静水時の速さを1.5倍にして下ったところ、9時間かかりました。この川の流れの速さは時速何㎞ですか」といった問題。

　川の長さも、上り下りにかかった時間もわかっているので、解答の材料は十分にそろっていますが、ポイントとなるのは、「静水時の速さが1.5倍になった」というところです。ここですぐに、上りの際の静水時の速さを②、下りの際の静水時の速さを③とおけるようになることが、このタイプの問題で確実に正解を得るために必須となります。

　この、数値をマルで記号化する解き方は、来月のマンスリー算の範囲となる相当算などでも多く使いますので、今回の演習を通して早めに慣れておきましょう。

　上り、下りの速さをマルでおき、変わらない流速を含めた式を立てれば、あとは消去算の考え方で、式どうしの足し算をすれば、流速を消すことができます。これは同じ流速の川での「出会いの旅人算」でも使う考え方です。

　比の考え方を使って数値を記号化して、式を足したり引いたりして解き進める、という流れを確実に身につけておけば、テスト中盤で出題される可能性の高い流水算の問題で得点できるチャンスが大きく広がります。

　このタイプの問題は、比を利用することで、わかっている数値が少なくても答えを求めることができるという、「比のメリット」を活用できる問題のひとつです。解き方の流れをしっかり確認しておきましょう。

【第5位　縮尺：ミスを防ぐための分数計算は正確に行えていますか？】

　「比と図形」の中に含まれる「縮尺」は、平面図形の単元ではありながら、相似や面積比のような与えられた図形の中にある比の関係を見つけ出す視点は必要とせず、単位換算と多数のゼロを処理する計算さえ正確に行えれば、大きな負担なく正解に行き着けるタイプの問題です。

　それだけにテストでの全体正答率も高くなる傾向にあり、今回のマンスリーでも「必答問題」に分類されます。それに加えて、他の単元の問題に少しでも多くの時間を費やせるように、スピーディーに処理することも求められる問題となります。

　確実に得点するために必要となるのが、分数式を使った計算です。これは塾でも何度となく説明されていることで、すでに習得されているお子様も多くおられると考えられますが、必答問題で取りこぼしがないように、改めて計算方法を確認しておきましょう。

　注意すべきは、ゼロの扱いで、縮尺の問題のほとんどが、平方cmと平方kmの単位換算を使います。その際に、(100×100)×(1000×1000)で、合計10個のゼロを扱うことになります。例えば「縮尺1/30000の地図上で、たて12cm、横15cmの長方形で表される土地の実際の面積は何平方kmですか」といった問題で、分数式をつくる場合を考えてみましょう。

　この場合は分母に、100×100×1000×1000を置くのですが、これを10000000000と積のかたちで書いてしまうと、ゼロの数が足りなくなるなどの思わぬミスが起こってしまいがちです。100×100×1000×1000と分割したかたちにすることで、正確にゼロを消す作業を進められます。

　もちろん、ゼロを10個並べて書く方法に慣れていれば、あえて書き方を変更する必要はありませんが、この縮尺の問題は何としても得点したい単元ですので、少しでもミスを減らす可能性が高い解法を使うことを心がけてください。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。