メールマガジン宝箱 Mail magazine

　今回の新6年生新学年グノーブル実力テストは、これまで習ったすべての単元がテスト範囲となります。重要単元について理解が曖昧になっているところは、この実力テスト対策を通して早めに復習を進めておきたいところです。

　特に単元を問わず重要となるのが「比」を使った解法を使いこなすことです。「旅人算」をはじめとした速さの問題、「面積比」「相似」といった図形の問題、そして「相当算」「倍数算」などの「比と割合の文章題」で、問題内容に応じた比の活用ができているか、そのための図の利用がスムーズに進められているか、徹底的に見直しておく必要があります。

　これまでの演習で身につけてきた力が総合的に試される新学年グノーブル実力テストの対策ポイントを、第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの算数予想問題と組み合わせれば、グノーブル実力テスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　平面図形：高さ共通な図形での「面積比＝底辺の比の関係」を使いこなせていますか？】

　平面図形の問題では、円やおうぎ形の複合図形の面積を求める問題や、図形が他の平面図形の周囲を回転移動する問題、複数の図形が重なり合った図形の中の角度を求める問題など、様々な単元からの出題が予想されますが、特に注意しておきたいのが、「相似形」「面積比」といった比を使って解くタイプの問題です。

　「面積比」の単元からは三角形や四角形を分割するタイプの問題や、逆に辺を延長させて新たな図形を作るタイプの問題などが出されますが、「高さが共通な場合は、面積比＝底辺の長さの比」が大前提となる点は共通しています。

　まずは、三角形を頂点と底辺上の1点を結んで図形を分けるタイプの基本問題について、問題を見た瞬間に比を使って面積比を求められるようにしておきましょう。ここで比の使い方が思い浮かばない場合は、すぐに『面積比』のテキストに戻って復習を進める必要があります。

　そのうえで下の左の図のような、三角形を辺上にある点を結んで切ってできる図形と、もとの三角形の面積比を正確に求められているかどうか、しっかりチェックしておきましょう。公式のように分数のかけ算で式を立てられるようにしておくことが大事ではありますが、この求め方も基本に「高さが共通な場合は、面積比＝底辺の長さの比」があることを踏まえておけば、式の立て方を忘れた際にも、図の点線のような補助線を引くことで対応できます。

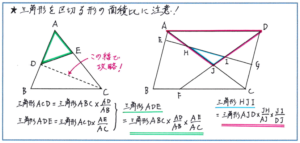
　この大きな三角形を区切って小さな三角形を作るというケースは、右の図のような、長方形や平行四辺形の中に複数の直線が引かれた場合にも使うことがあります。三角形の向きが変わっても正しく対応できるように、まずは基本の形をしっかり覚え込んでおきましょう。

【第2位　相似形：1つの直線を2種の比で分ける解法は確実に使いこなせていますか？】

　「相似形」の問題もまた、今回の実力テストで間違いなく出題される平面図形・最重要単元のひとつです。その出題パターンは多岐にわたり、問題の難度も幅広くなりますが、基本となるのは「平行線」に着目することです。

　まずは基本的な砂時計型やピラミッド型のように、与えられた平行線から相似の関係を見出す基本パターンを確実におさえ、さらには、相似の関係にある図形の相似比がa：bの場合、面積比が(a×a)：(b×b)、体積比が(a×a×a)：(b×b×b)となる点までしっかり理解を固めておきましょう。

　そうした基本的な内容からさらにレベルアップした問題として、長方形や平行四辺形、台形を素材として相似の関係を的確につかむ力を求める問題があります。それらの問題は、実力テストの中盤から後半に出てくる可能性が高く、得点の分かれ道になる重要単元となります。

　その中でも特に注意しておきたいのが、例えば下の図の平行四辺形ABCDの中に2本の直線がひかれていて、与えられた線だけで作られるもの以外の相似の関係を作り出すケースです。ここでは、辺ADと辺BCが平行であることから、「あと一歩でクロス型の相似になる」と考えることが、正解への大きなステップになります。ADとBEをそれぞれ延長させた線の交わる点をGとすれば、AGとBCが平行なことから、三角形GDEと三角形BCEが相似となります。

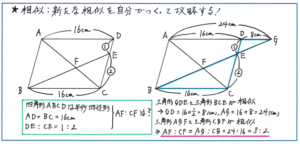
　さらに、三角形AGFと三角形CBFも相似になります。ここでDE：CE＝1：2であるため、ADの長さが16cm、DGの長さが16×1/2＝8（cm）より、AF：CF＝AG：CB＝(16＋8)：16＝24：16＝3：2と、AF：CFの比を求めることができます。

　この「線を延ばして新しい相似の関係をつくる」という作業は、一見手間がかかりそうですが、相似の関係さえつくってしまえば、比や長さが次から次へとわかって行きます。平面図形の応用問題での正解率を上げるためにも、この解法の流れをがっちりとつかんでおきましょう。

【第3位　速さの問題：グラフを読み取り、活用する解き方を身につけられていますか？】

　速さの問題もまた実力テストにおいて、旅人算、通過算、流水算、時計算といった主要単元から様々な問題が出されることが予想されます。速さの問題は言うまでもなく入試頻出の最重要単元のひとつですので、この実力テスト対策を通して、速さの苦手分野がないかチェックをして、徹底的に復習しておきたいところです。

　まずは、例えば流水算での「上りの速さ」「下りの速さ」「川の流れの速さ」の関係や、時計算での角速度の使い方などの基本事項をしっかり覚えられているかを確認しておきましょう。そして、特に旅人算や通過算で、動きの様子を整理するための図が活用できているかどうか、テキストやこれまで受けたグノレブやの解説を見直してチェックしておいてください。

　その上で特に重要となるのが、「比」を使った問題で確実に得点することです。例えば通過算で電車が通過する鉄橋の長さが2：3といった比で表されるパターンや、流水算で静水時の速さが5/2倍に変化するパターンなど、速さの中で比を使う問題には多くのパターンが見られます。これらの問題についても、これまでの演習やグノレブで間違えた問題、正解はしたけれど比の使い方に確信が持てなかった問題を中心に解き方の確認を徹底しておきましょう。

　そして、問題を解く際に、線分図やグラフを自分でかいて解答の糸口をつかむことができているのかも要チェックです。特にグラフについては、まずは正確な読み取り（問題文の要素がどのようにグラフに反映されているのかをつかむこと）ができているかが重要となります。そのためにもグラフの中に適切な「かき込み」ができているか、そのかき込みが雑になっていないかをしっかり見直しておきましょう。

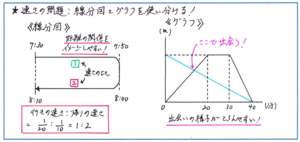
　実際に実力テストで、グラフを完成させる問題が出される可能性は高くありませんが、問題で提示されたグラフに新たなグラフをかき入れることで解答方針が立てられるケースが多くあります。何より、グラフを自分でかくという視点に立つことで、グラフから情報を読み取る練習にもなります。普段から簡単にで構いませんので、グラフをかく練習も重ねておきましょう。

【第4位　立体図形：水深変化の問題を「断面図」で解き進められていますか？】

　立体図形の問題では、円柱や円すいといった図形の体積、底面積を求める基本中の基本の問題、回転体の問題や投影図の問題といった自分で立体の図をかくことが必須となる問題など、幅広いパターンでの出題が予想されます。

　その中でも「水深の変化」の問題は、立体図形の単元だけでなく、グラフと結びつけて解答を進める点で速さの要素が含まれることもあり、問題の難度が上がるケースが多く見られます。出題パターンとしては、水を入れる水そうの形が「仕切りが入った形」や「腰かけの浴そうの形」であるケースが多く出題されますが、いずれの場合にも共通して有効となるのが、水そうを真正面から見た「断面図」のような平面を使って考える解法です。

　水そうの形が、仕切りが入ったり、段差がついたりすることで複雑になっても、「奥行きの長さ」が一定であるケースがほとんどです。そこで、立体の体積を一定の奥行きの長さで割って求められる平面で考えることができるのです。

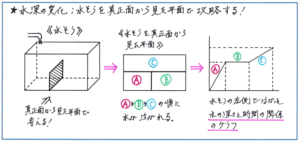
　断面図で考えることによって、上の図のＡの部分とＢの部分に水が入る時間の比（水が一定の割合で水そうに入るとします）が、ＡとＢの長方形の横の長さの比とすることができ、Ａ＋Ｂの部分とＣの部分に水が入る時間の比が、それぞれの長方形のたての長さの比とすることができるため、比を使った解法をスムーズに進めることができるのです。

　イメージのしづらい立体図形の問題も、平面図形で表現することで、比の利用など使える解法の幅が一気に広がります。立体図形の問題を平面図形で攻略する方法をどんどん増やしておきましょう。

【第5位　比と割合の問題：問題内容に合わせて適切に図を利用できていますか？】

　比と割合の問題を攻略する上で重要となるのが、正確な式を立てることですが、そのためにも問題内容を正確に整理する必要があります。実力テストでは、問題文が数行にわたり、どの情報をどのように使えばよいか瞬時に判断できないような問題がテストの中盤に出されることがあります。そこでの得点がテスト全体に影響を及ぼすことが必須なだけに、問題内容を正確に整理することは必須の条件となるのです。

　そこで問題内容の整理に不可欠となるのが線分図や面積図といった「図」の活用です。特に食塩水の濃度の問題での面積図のかき方は徹底的に固めておく必要があります。面積が等しい長方形のたての長さと横の長さの逆比の関係を瞬時に見つけ出し、式にする流れを今のうちに定着させておくことで、今後、様々な単元で何度も利用することになる強力なツールを使いこなせるようになります。

　また、比と割合の問題の重要単元のひとつであるニュートン算もまた、線分図の効果が大いに発揮される問題を多く含みます。出題パターンが限定されるニュートン算だからこそ、線分図から立式の流れを着実に身につけておけば、得点源にできるチャンスが大きく広がります。

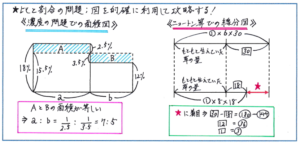
　もちろん、比と割合の問題のすべてで図を使う必要はなく、問題内容によっては図を経由せずに立式に至ることができるものもあります。図を必ず使わなくてはいけない、といった意識を持つことなく、あくまで有効な武器として図を使える体勢をとれるように、図を的確に使う判断ができるように、普段から図をかく練習を重ねておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。