メールマガジン宝箱 Mail magazine

　5年生最後の組分けとなる今回の新学年組分けテストで目標を達成して、万全の構えで新年度をスタートさせたいところです。ただ、これまでに習ったすべての単元から範囲なしで出題される組分けテストですので、どこに復習のポイントを定めればよいのか迷ってしまいます。

　さらには5年の夏以降には、「速さ」や「平面図形」をはじめとした入試頻出の重要単元も多く学習して来ましたので、これまでの組分けテストと比べて難度が大幅にアップする可能性が高くあります。

　そこで、幅広い範囲の中でも特に出題頻度が高く、注意すべき単元を中心に、新学年組分けテストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの「50分で偏差値を5上げる算数予想問題」 と組み合わせれば、組分けテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　速さの問題：問題に合わせて状況図とダイヤグラムを使い分けられていますか？】

　組分けテストでは「速さ」の単元から難度の高い問題がテスト終盤に大問として出される傾向があります。その難度の高さは、複雑な計算が求められるというよりもむしろ、長い問題文から内容を正確に把握する力が試される点にあります。

　その長い文章の中で、どのように動きが展開するのか、時間を追った変化を確実につかむことが問題を解くうえでの大前提となり、変化をつかめれば問題の難度は一気に下がります。そうした、一見複雑な問題文を正確に読み解くために必要となるのが「状況図（線分で動きを示す図）」や「グラフ」です。問題の内容に応じてどのような図・グラフを選べばよいのか、その判断をスピーディーに行うことが問題攻略のポイントになります。

　特に旅人算は、通過算や流水算と比べて問題のバリエーションが豊富なだけに、どのように状況図・グラフを使うかで迷ってしまいがちです。この出題パターンであればこのタイプの状況図（グラフ）を使う、といった定型こそありませんが、状況図・グラフそれぞれのメリットをおさえておくと、どちらを使うかの判断がしやすくなります。

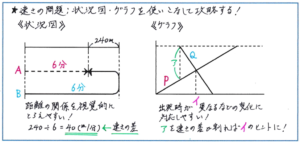
　状況図は、グラフと比べて線分図を複数かき込めばよいので、作図がしやすいうえに、「距離の関係」を視覚的にとらえやすいため、例えば離れた地点にいる2人が向かい合って出会う場合や、同じ地点から出発して一方が折り返して出会うといったパターンで効果を発揮します。

　ただし注意すべきは、その効果がより発揮されるのが「速さが一定」である場合ということです。動く途中で速さが変わる場合、その様子を状況図で詳しく表すことは困難であり、図が複雑になり過ぎてしまいます。

　それに対して、速さが途中で変わったり、一方が途中で休むといった、「一定ではない動き」を視覚的に把握する際に大きな効果を発揮するのが「グラフ（ダイヤグラム）」です。またバスのように定期的に往復運動をする状況を表す場合も、グラフ（ダイヤグラム）を使うと、動きが視覚的に把握しやすくなります。

　組分けテストで出されるような難問のレベルになると、図・グラフの必要性がより一層増します。少し手間はかかっても図・グラフで問題内容を整理できれば、大問の中でも小問で解答できるチャンスが一気に広がります。問題内容を図・グラフで整理する時間を少しでも短縮させるために、普段から作図する練習を重ねておきましょう。

【第2位　平面図形：面積比や等積変形・等積移動を正確に使って面積を求められていますか？】

　平面図形から組分けテストの出題対象となる単元は多々あります。まず注意しておきたいのが、「相似」や「面積比」といった、「比」を使って解く問題です。相似であれば、まずはピラミッド型や砂時計型の基本型を図形の中からスピーディーに見つけ出せるように、過去のテストを見直して「平行線」に着目して図形を見る視点を鍛えておきましょう。

　面積比については「高さが共通な図形の面積比は底辺の長さの比と等しい」という大前提を徹底的に意識できるように気をつけておきましょう。特に注意しておきたいのが、平行四辺形の面積を台形の公式で解く方法です。例えば下の左の図のような、台形の面積と平行四辺形の面積の関係が与えられた状況で長さを求めるケースで使えることが多く、これから面積比の問題が多く出されるに連れて、その重要性がさらに増して行きます。

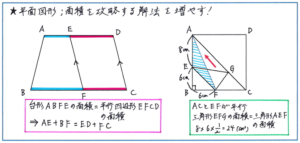
　また、上の右の図のような、与えられた図形の形を変えることで面積を求める等積変形や、別の位置にある同じ面積の図形に着目する等積移動といった解法も、テスト中盤の図形の小問集合や、終盤の大問の中の1問といったかたちで出されることが多くあります。特に等積変形では、平行線の存在に気づけば変形がわかりやすくなります。相似と同じく、平行線が重要な役割を担うことを強く意識しておいてください。

【第3位　立体図形：立体図形→平面図形と切り替える解き方は身についていますか？】

　立体図形もまた平面図形と同じく様々な単元からの出題が予想されますが、単元を問わず有効な解法となるのが、「立体図形を平面として見て考える」方法です。

　特にその解法が有効となるのが「水深変化」の問題で、水そうにおもりを入れるパターンや、水そうの中に仕切りがあったり、水そうに段差があるようなパターンでは、水そうを真正面から見た「断面図」のような平面で考えると、時間の経過と深さの変化の関係や、比の活用をスムーズに進めることができます。

　水そうに仕切りや段差があるパターンではグラフが合わせて提示される出題が多く見られますが、平面で変化をとらえることで、グラフとの関係性もより明確に見えるようになります。

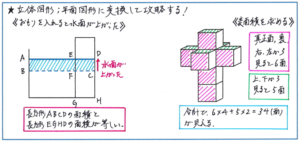
　また、上の右の図のような、小さな立方体を組み合わせてできる立体の表面積を求める場合、立体を上下左右、正面、裏の6面から見た際の見える正方形の個数で考える方法もまた、立体図形を平面図形に切り替えて考えるパターンのひとつです。

　平面図形に比べて図形のイメージがつかみづらい立体図形の問題を攻略するうえで、平面図形への切り替えは重要な解法となりますので、しっかり復習しておきましょう。

【第4位　場合の数：該当するケースを正確に書き出すためのルールを守れていますか？】

　場合の数の問題では、問題の難度に関わらず、当てはまるケースをもれなく挙げることが必須となります。そのためには、書き出しと計算を正しく組み合わせる解法が必要です。書き出しを行う際に、ただ闇雲に数を並べてしまうと、思わぬところでもれが発生してしまいます。正しいルールにしたがって書き出しを進めることが大前提となるのです。

　例えば、「5個のリンゴをAさん、Bさん、Cさんの3人で分けるとき、リンゴの分け方は全部で何通りありますか。ただし、1個ももらわない人がいてもよいものとします。」といった問題を例に、書き出しの方法を考えてみましょう。

　ここで、Aさんが3個、Bさんが1個、Cさんが2個、次に、Aさんが1個、Bさんが4個、Cさんが0個…と、何のルールもなしに分け方を挙げてしまうと、解き方が煩雑になるうえに、ミスが起こりやすくなってしまいます。

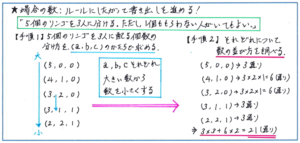
　そこで、「大きい数から当てはめて行く」というルールにしたがって進めてみましょう。下のように、まず5個のリンゴを3人に配る個数の分け方を（a、b、c）のかたちで整理します。この際に、まずはaに当てはまる数を大きい順に5から入れて、b、cには5以下の数を入れるとして進めて行きます。aが5の場合は、b、cともに0という（5、0、0）の1つのケースしかありませんので、次にaが4の場合を考えます。aが4の場合は、残りが1個になりますので、b＝1、c＝0とします。

　ここでは数の組合せを挙げることが目的ですので、b＝0、c＝1のケースは含めずに、（4、1、0）として、次に進みます。

　aが3の場合は、残り2個を分けますので、ここでもbに当てはまる数を大きい2から始め、（3、2、0）を挙げ、さらにb＝c＝1である（3、1、1）とします。aが2の場合は、（2、2、1）のみが当てはまります。aが1の場合は、b、cがaより大きくなってしまいますので、当てはまるケースはありません。

　このようにして挙げた（5、0、0）、（4、1、0）、（3、2、0）、（3、1、1）、（2、2、1）それぞれのケースについて、数の並び方を調べると、（5、0、0）は5の入る位置によって3通りに、同じく（3、1、1）、（2、2、1）も3通りとなります。（4、1、0）、（3、2、0）は3種類の数の並び方になりますので、3×2×1＝6（通り）となり、合計して、3×3＋6×2＝21（通り）と求めることができるのです。

　場合の数では、書き出しでもれが発生してしまってもそれに気づかずに解き進めてしまうことで、失点につながるケースが多く見られます。また、割合や速さの文章題のように、求めた答えを当てはめて確かめをするといった見直しもできないところに、場合の数の難しさがあります。

　正確にかつスピーディーに得点するためにも、ルールにしたがって書き出しをする練習を重ねておきましょう。

【第5位　数の性質：基本ルールを覚え込んで、確実な得点源にしましょう！】

　最小公倍数の利用や既約分数の問題など、数の性質からも幅広い単元が出題対象となりますが、まずは素因数分解をはじめとした基本ルールを使いこなせているかどうか、綿密にチェックしておきましょう。過去のマンスリーでの解答を振り返り、ルールの使い方が少しでも曖昧な場合は、解説をよく読んで解答の流れを頭の中にインプットしておいてください。

　特に、素因数分解を使った約数の個数の求め方や、「7で割ると3あまり、9で割ると5あまる数」といった公倍数の問題については、問題を見た瞬間に解法が頭の中に浮かぶように、復習を徹底しておく必要があります。後者の問題は、「4を加えると7と9の公倍数になる」という「足りない数が共通」のパターンですが、より基本的な「あまりが共通の問題」はもちろん、あまりも足りない数も共通していないパターンでの数の書き出し方までしっかり対応できるようにしておきましょう。

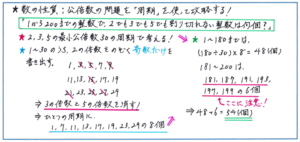
　また、例えば「1から200までの整数のうち、2でも3でも5でも割り切れない整数は何個ありますか」といった問題で、少しでも作業量を減らせる解法を習得しておくと、抜群の効果を発揮させることができます。

　ここでおすすめしたいのが、「周期」を使った解き方です。今回の問題であれば、2と3と5の最小公倍数である「30」を1つの周期として、1から30までに「2でも3でも5でも割り切れない整数」が何個あるか調べて、その周期が1から200までに何個あるか、といった流れで解き進める方法です。

　もちろん、このタイプの問題では、2の倍数、3の倍数、5の倍数、そしてそれぞれの公倍数の個数を求めて、集合のベン図を使って解く方法を使うこともできます。ただ、求める値の種類が多くなり、求めた数値がベン図のどの部分にあたるのかを正確に判断するといった、全体の作業量が多くなるため、自ずとミスをしてしまう可能性も高くなってしまいます。

　限られた時間内に少しでも多くの問題を解くために、短縮できる時間を少しでも多く作り出すことは、組分けテストだけでなく、今後のテスト、模試、そして入試においても鉄則となります。そのためにも、解法のバリエーションを広げておく準備を重ねておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。