メールマガジン宝箱 Mail magazine

　5年生最後の組分けとなる第9回組分けテストでは、「速さの問題」、「立体図形」、「濃さと比」といった、入試頻出の重要単元ばかりがテスト範囲となります。特に比を使った難度の高い問題で、解法を正しく使いこなすことが偏差値をアップさせるうえで必須となります。

　新6年生を今よりも上位のクラスで迎え、よりよいかたちで受験最終学年のスタートを迎えるための大事なテストですので、万全の対策をしておきたいところです。そこで、第9回組分けテストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの「50分で偏差値を5上げる算数予想問題」と組み合わせれば、組分けテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　速さと比：グラフの中の三角形を使って速さの比を求める方法を習得できていますか？】

　今回の組分けテストでは、入試頻出の重要単元「いろいろな速さの問題」がメイン単元のひとつとなりますが、その中でも「速さと比」については難度の高い問題が出される可能性が高くあります。

　旅人算、通過算、流水算、時計算それぞれの基本的な解法をしっかりおさえたうえで、そこに「比」の要素が含まれた場合にどれだけスムーズに対応できるかが、得点アップのポイントになります。

　まずは「道のり」「速さ」「時間」の3要素について、「時間が同じならば、速さの比＝道のりの比」、「速さが同じならば、時間の比＝道のりの比」そして「道のりが同じならば、速さの比＝時間の逆比」の関係は確実におさえておきましょう。

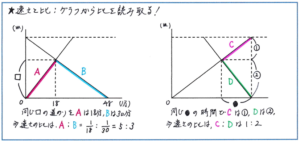
　特に「速さの比＝時間の逆比」は、組分けテストはもちろん、実際の入試問題でも頻出の考え方ですので、問題を見た瞬間に比の関係が思い浮かべられるように、理解をしっかり固めておいてください。

　さらに、この逆比の関係をグラフから正確に読み取る力も今回の組分けでは求められます。『予習シリーズ5年下』第18回の196～197ページの［例題6］にある、グラフの中の三角形を使って速さの比を求める流れは、とても重要ですので、解説を熟読したうえで解法を習得しましょう。

【第2位　濃さと比：面積図を使いこなして、食塩水の混合の問題を解くことができていますか？】

　食塩水の濃さの問題は、割合と比の単元の中でも特に入試問題での頻出度が高く、今回の組分けテストでも十分に対策を積んでおくべき単元のひとつとなります。まずは「食塩水の量」「食塩の量」「濃さ」の関係を示す基本的な式についての理解が大前提となりますので、そこが不十分な場合はすぐに『予習シリーズ5年上』の第6回に戻って復習しておきましょう。

　そうした基本をおさえたうえで、今回の組分けでは「比」の要素が含まれるレベルアップした問題が出題対象のメインとなりますので、ひとつひとつの解法を正確に理解しておく必要があります。特に注意すべきは、「食塩水の混合と比」の項目で演習する、面積図を使った解法です。面積図は食塩水の濃さの問題だけでなく、平均算をはじめ多くの重要単元で使うことになりますので、今回の組分け対策を通して、面積図のかき方を完全にマスターしておくようにしましょう。

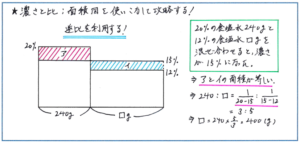
　どの単元においても、面積図の基本は2つの要素のかけ合わせを「長方形の面積」に当てはめることにあります。濃さの問題では、「食塩水の量×濃さ＝食塩の量」であることから、長方形のたての長さを濃さに、横の長さを食塩水の量として、食塩の量を長方形の面積とします。ポイントは同じ面積の長方形のたての長さと横の長さが逆比の関係にあるこです。この逆比の関係を瞬時に使いこなせるように、面積図をかいてから式を立てるまでの流れを、練習を通して身につけておきましょう。

　面積図を使いこなせれば、複雑な小数計算を使う手間が省けますので、正答率は上がり、解答速度もアップさせることができます。

【第3位　回転体と比：相似比から求められる体積比を使った解き方を使いこなせていますか？】

　回転体の問題では、5年最後の組分けテストにもなると、単純な円柱や円すいよりも難度が上がった、円すい台（プリンのような形）のような応用型の図形が出される可能性が高くあります。そうした問題で解き方の工夫ができるかどうかが、テスト全体の点数に大きく影響を及ぼします。今回の組分けでは、「比」を使って解く問題の出題割合が高くなりますが、この回転体の問題でも比を使って解く問題に注意が必要になります。

　回転体の中でも、特に円すい台の問題では、大きな円すいの体積から小さな円すいの体積を引く、といった解法ではなく、『予習シリーズ5年下』の185ページでも紹介されている、「相似比から求められる体積比」を活用する力が試されます。円すいどうしの引き算ではなく比を使った場合、分数を使うことになって計算が複雑になるのではないか、と躊躇してしまうかもしれませんが、分数が約分できれば、式は一気にシンプルになります。何よりも複雑なかけ算を2回行ったうえで、それを引き算するといった手間と比べると、圧倒的に進めやすく、ミスも起こりにくくなります。

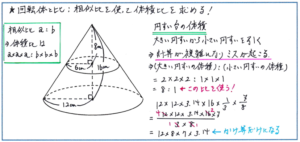
　お子様が大きな円すいの体積から小さな円すいの体積を引く解法で進めていた場合は、すぐに解法を変えるのではなく、まずこれまで通りの解法で答えまで行き着いた後で、体積比を使った解法で解き直してみてもよいでしょう。そうすることで、体積比を使うという工夫の効果をより強く感じる効果が得られます。

【第4位　投影図：見えない部分を逃さずに表面積を正しく求められていますか？】

　立体図形の中でも、「投影図」の問題では、複雑な立体が素材となるケースが多く見られます。そうした立体の表面積を求める際には、解答方針をしっかりと立てたうえで、見逃してしまう部分がないように、気をつける必要があります。

　まずは『予習シリーズ5年下』の181ページで紹介されている、「図形を6方向から見た図で考える」という解法を使いこなせるようになることが必須となります。これが「くぼみ」のない立体であればスムーズに対応できるところですが、例えば下の図のような、「見えない部分」がある場合には慎重に取り組み必要があります。

　重要なのは、自分で図をかくことにあります。予習シリーズの例題では、3方向から見た図をかく小問が設定されていますが、実際の組分けテストでは、そうした小問がないパターンが多く、問題の誘導なしに、すぐに自分で図をかけるように、普段から練習を重ねておかなくてはなりません。

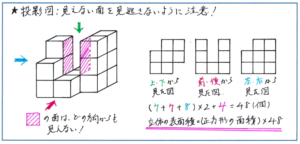
　その際に、上のように見えない部分を強調しておけば（テストでは色ペンはもちろん使えませんので、印をつけるだけでOKです）、見逃すリスクを防ぐことができます。もともと見えない部分がイメージしづらい点が立体図形の難しさですが、まさにこのタイプの問題は、その見えない部分を把握する力を求めるものですので、テストで出される可能性が高く、また得点差を生む問題となります。普段から自分で図をかく練習をしっかり重ねておいて、テスト会場で落ち着いて対応できるようにしておきましょう。

【第5位　速さと比：通過算・流水算・時計算それぞれに対応した図を活用しましょう！】

　5年の夏期講習で基本的な考え方を学習した速さの重要単元「通過算・流水算・時計算」について、難度をアップさせた問題が今回の組分けテストの出題対象になります。

　問題の難度は上がっても基本的な考え方が大前提となる点には変わりありませんので、まずはそれぞれの問題の内容を整理するための図が正確にかけているか、確認をしておきましょう。速さの問題の中でも通過算であれば「長さのあるものが動く様子」を、流水算であれば「速さが変化する様子」を、時計算であれば「角速度」について、図をつかって正確に把握することが解答の糸口をつかむきっかけとなります。

　図をかく手間を面倒に感じてしまうお子様も多いですが、速さの問題は視覚的に状況を把握できるかどうかで、解答の進めやすさに断然の差が生まれます。できるだけ時間をかけずに、ポイントを把握できる図をかけるように、普段からスピーディーに正確な図をかく練習を重ねておきましょう。

　3つの単元の中でも、「比」という点では、特に通過算・流水算に注意が必要です。通過算では、通過するトンネルや鉄橋の長さが比で表される基本パターン以外にも、様々なかたちで比の活用が求められます。

　その中でも気をつけておきたいのが、「列車の長さと、速さの比を使って同じ距離を進む列車の時間の比を求める」パターンです。例えば、「長さ120mの列車Aと長さ180mの列車Bがあり、2つの列車の速さの比は2：3です。列車Aと列車Bが長さ600mのトンネルを通過するのにかかった時間の比を求めなさい。」といった問題で、解き方を考えてみましょう。

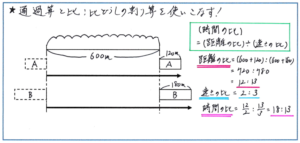
　ここで使うのが、(時間の比)＝(距離の比)÷(速さの比)の考え方です。距離の比は、(600＋120)：(600＋180)＝720：780＝12：13で、速さの比が2：3であることから、時間の比は、12/2：13/3＝18：13と求めることができます。

　距離に列車の長さを含める点が通過算ならではのものですが、使う考え方は速さの比の基本と変わりありません。

　また、流水算であれば、船の静水時の速さ、上りの速さ、下りの速さ、そして川の流れの速さといった複数の速さについて、その関係が比で表される問題で注意が必要となります。

　同じ長さの川を上った際の時間と、下った際の時間が与えられ、そこから逆比を使って上りの速さと下りの速さの比を求め、さらに、「川の流れの速さ＝（下りの速さ－上りの速さ）÷2」あるいは「静水時の速さ＝（下りの速さ＋上りの速さ）÷2」の式にあてはめて、川の流れの速さや静水時の速さの比を求める、また、川の長さを求めるという流れは、文章にすると複雑に感じられますが、テストで頻出の典型パターンですので、確実に解法の流れをおさえておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。