メールマガジン宝箱 Mail magazine

　今回の4月度マンスリーテストは、マンスリーではありますが、春休みに演習した割合や平面図形、立体図形などの重要単元が幅広く出題対象となり、さらには速さも範囲に含まれるといった実力テストに近い内容となります。重要単元が勢ぞろいで、どこから復習を進めればよいか迷ってしまうところですが、各単元の解答ポイントをしっかりつかめば、クラスアップのチャンスは十分にあります。

　そこで問題内容を正確に整理するための解法を中心に6年4月度マンスリーテストの対策ポイントを第1位から第5位までランキングにしましたので、ぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの「50分で偏差値を5上げる算数予想問」と組み合わせれば、マンスリーテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　速さのグラフ：速さと時間の逆比の関係をグラフから正確に読み取れていますか？】

　6年生になると、テストで出される「速さの問題」の難度が大きくアップします。その主たる要因は比を利用して解く力が求められる問題が増えてくることにあります。そのためにも速さと比の考え方を今回のマンスリー対策を通して、固めておきたいところです。特に速さに関する「逆比」の考え方を確実に理解し、使いこなせられるようになれば、テストの終盤で出されるような複雑な応用問題でも正解できるチャンスが大きく広がります。

　進む距離が同じであれば、速さと時間が逆比の関係にあることは、速さと比の問題を解く上で基本中の基本であり、例えば「学校から公園までA君は30分、B君は45分で進みました。A君とB君の速さの比を求めなさい。」といった基本問題であれば、1/30：1/45＝3：2と、時間をかけずに速さの比を算出できるようになっておかなければなりません。

　6年生のマンスリーで得点差がつくポイントとなるのは、逆比の関係を問題文、特にグラフの中から、いかに速く的確に見つけ出すか、ということになります。

　例えば下のようなグラフの中から比の関係をスムーズに見つけ出すことができているでしょうか。グラフを見た瞬間に、赤と青で囲んだ線でできる三角形の相似の関係が見つけられるでしょう。グラフの中からこの砂時計型の相似の関係を見つけ出すことは基本ですので、この点で戸惑うことがある場合には、速さとグラフの基本を急ぎ復習しておきましょう。

  さらに別の箇所に目を移すと、緑とピンクの斜線が入った部分の三角形に重要な比の関係が表されています。この2つの三角形は図形として高さが共通になっています。グラフにおける高さ（たての長さ）は「距離」を表します。よって、「同じ距離を進む場合は速さと時間が逆比の関係」の考え方を使うことができるのです。2人が出会うまでの距離を進むのに、Aはa分、Bはb分かかっていますので、ここから2人の速さの比が、1/a：1/b＝b：aと求めることができます。

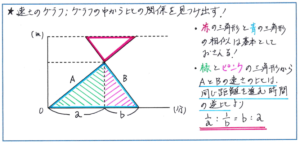
　速さとグラフの問題では、問題文やグラフからどこまで数値が得られるかによって、利用する比の関係が決まってきます。上のグラフでも赤の三角形と青の三角形の底辺にあたる数値がわかれば、赤と青の相似の関係が使えますし、aとbにあたる数値がわかれば、逆比の関係を使うことができます。

　まずは問題文を読んで、そこでわかる数値をグラフにドンドン書き込むことを習慣として身につけておきましょう。6年生のテストでは単元に関わらず、手を動かして問題内容を整理する姿勢が必須となります。しっかり練習を重ねておきましょう。

【第2位　平面図形：解答のポイントを見つける補助線を引くことはできていますか？】

　平面図形の問題では、図形の中から「相似」と「面積比（高さ共通の図形での面積比は底面比と等しい、など）」という2つの要素を的確に見つけ出すことがポイントになりますが、6年生になって問題の難度が上がってくると、ただ与えられた図形を見ているだけでは要素の見つけ出しがスムーズに行かなくなります。

　そこで重要となるのが補助線の引き方です。補助線を引くことによって、そのままでは見つけられなかった新たな相似の関係を作り出すこと、面積比を利用しやすいかたちにすることが可能となり、正解への道筋がよりはっきりと見えてくるのです。

　例えば下のような、三角形ABCの中の三角形AEFと三角形CDEの面積、そしてAF：BEとBD：CDが与えられた状態で、AE：CEを求めさせる問題の場合には、どこに補助線を引けばよいでしょうか。

　求めるのはAE：CEなので、AEとCEをそれぞれ底辺として高さが等しい、三角形ABEと三角形CBEの面積比が求められればよいことがわかります。そこで、BとEを線で結んでみましょう。AF：AB＝2：(2＋3)＝2：5より、三角形ABEの面積は、10×5/2＝25（平方cm）、BD：BC＝1：(1＋2)＝1：3より、三角形BCEの面積は、36×3/2＝54（平方cm）となるため、AE：CE＝(三角形ABEの面積)：(三角形CBEの面積)＝25：54と求められます。

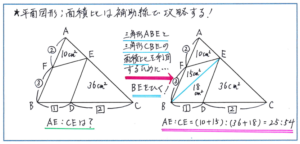
　補助線を引く際にまず注意すべきは、相似や面積比の「基本パターン」を活用できるかたちにすることです。今回ご紹介した問題でも、面積比＝底辺の長さの比という基本パターンが習得できていれば、三角形の面積比を利用するという考え方をすぐに思い浮かべることができます。

　相似でも、相似の基本パターンを作り出すことを念頭に置けば、補助線が断然引きやすくなります。SAPIXのテストでは、これから図形の問題の難度がどんどん上がってきますが、基本パターンさえ把握できていれば、補助線を引くなど積極的に手を動かすことで、そうした難問でも攻略の糸口がつかめるようになります。相似、面積比の基本パターンが理解できているか確認すること、基本パターンを見つけ出すために図へのかき込みを行う意識を強く持つことを徹底しておきましょう。

【第3位　割合と比の文章題：仕事算で解きやすいの式の立て方ができていますか？】

　今回のマンスリーでは割合と比の文章題からも様々な問題が出されますが、特に仕事算では式の立て方と、そこからの比の利用をスムーズに進められるように練習を重ねておく必要があります。

　例えば、「A、B、Cの3人がある仕事をします。この仕事は、Aが20分した後に、Bが9分すると仕上がります。また、Aが10分した後に、Bが15分しても仕上がります。Bが12分でする仕事の量を、AとCの2人がすると6分で仕上がります。この仕事をA、B、Cの3人がはじめから一緒にすると、仕事が仕上がるのに何分かかりますか。」といった問題。

　問題文が長く見えますが、仕事算の応用型ではいたって定番のパターンです。解答の方針として、最初の3つの文から、AとBとCの1分あたりの仕事量の比を求めることが大前提となります。ここで逆比の関係を使って式をスピーディーかつ正確に立てることがポイントになります。

　まず、A、Bの1分あたりの仕事量をそれぞれマルA、マルBとすると、全体の仕事量は、マルA×20＋マルB×9とマルA×10＋マルB×15の2つの式で表すことができます。ここから式の変形で一気に、マルA×10＝マルB×6とできればベストですが、式での処理が難しい場合は、下のように線分図で比の関係を求めることもできます。

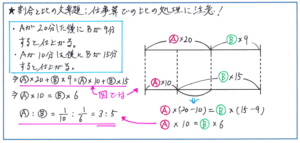
　ここからマルA：マルB＝1/10：1/6＝3：5となり、A、Bの1分あたりの仕事量をそれぞれマル3、マル5とすることで、Cの1分あたりの仕事量を、(マル5×12)÷6－マル3＝マル7と求めることができます。

　あとは全体の仕事量を、マル3×20＋マル5×9＝マル105と求めて、それをA、B、Cの1分あたりの仕事量の和である、(マル3＋マル5＋マル7＝)マル15で割ることによって、マル105÷マル15＝7（分）と、正解に行き着くことができるのです。

　今回は仕事算の典型的な応用パターンでしたが、別の問題で問題文が長く複雑に見えても、比・逆比という強力ツールを手に入れていますので、式の立て方に注意すれば、正解できるチャンスが大きく広がります。比を使った解法を確実に習得して行きましょう。

【第4位　場合の数：解き方を複数持っていると、難しい問題が断然解きやすくなります！】

　場合の数の問題では、解き方のパターンを複数覚えておけば、テストで解答にかける時間を一気に短縮でき、正解できる可能性がグンと高くなります。

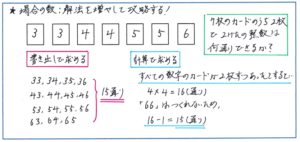
　例えば、「3、3、4、4、5、5、6と数字が書かれたカードが7枚あります。これらのうち、2枚のカードを並べて2けたの整数をつくるとき、整数は何通りつくれますか。」といった問題で、解き方を考えてみましょう。

　まずは地道に書き出しで解き進める方法です。2けたの整数は、33、34、35、36、43、44、45、46、53，54、55、56、63、64、65の「15通り」つくることができます。場合の数では、計算で解くことができれば、その方が時間を短縮できて確実と考えられがちですが、計算での解法についてすぐに思い浮かばない際には、すぐに書き出しを実践するようにしましょう。特にこの問題のように数の種類が4つでカードの種類が7枚と限られている場合には、書き出しに大きな負担がかかりませんので、正確さも確保できるでしょう。

　それに対して別の方法として、あてはまらないケースに着目することがポイントとなります。

　今回の問題では、3、4、5のカードは2枚ずつありますが、6だけは1枚となります。そこで、「もしもすべてのカードが2枚ずつあったとしたら」と仮定すると、2けたの整数は、「4×4＝16」より、16通りできることになりますが、実際の7枚のカードではつくることができない数、「あてはまらない数」が「66」となりますので、16－1＝15（通り）として求めることができます。

　この、あてはまらないケースに着目する解法は他にも例えば、2つのサイコロの目の和が10以下の場合、といった際にも、起こり得る全体の場合の数から、「和が11と12になるケース」を引いた方が早く求められるなど、様々な問題で使うことができます。

　問題内容に応じて解法を使いこなせるように、地道に解法を増やして行きましょう。そのためにはこれからのマンスリーや組分け、オープンで、解説に【別解】がある場合には、必ずそちらまでチェックする習慣を身につけるようにしましょう。

【第5位　流水算・通過算：問題内容を図を使って正しく整理できていますか？】

　春休み前に演習した「流水算・通過算」の単元からは、問題文が長く、内容の整理が難しい問題が出される可能性が高くあります。そうした問題を攻略するためには、図で内容を整理する作業が必須となります。

　例えば、次のような通過算の問題には、どのように対応すればよいでしょうか。

　「長さ120mで秒速25mの電車Pと、長さ240mで秒速35mの電車Qがあり、太郎君が2つの電車が走る線路と並行する道を自転車で走っています。太郎君の真横で電車PとQがすれ違いはじめ、太郎君の真横で電車Pと電車Qがすれ違い終わりました。太郎君は秒速何mで走っていましたか」

　単に電車PとQがすれ違う、あるいは、どちらかが一方を追いこすといった基本パターンであれば、あえて図をかかなくても基本公式で十分正解にたどりつくことができるでしょう。この問題では、そこに太郎君の動きという1つの要素が加わることで、難度が一気に上がっています。

　そこで図をかいて問題内容を整理するのですが、まずは太郎君の動きは入れずに電車PとQがすれ違いはじめてからすれ違い終わるまでの様子を図にして、そこに太郎君の動きを加える、という流れで進めることにしましょう。この問題に限らず、まずは整理しやすい情報から図にかき込むようにすると、複雑な内容でも図に表しやすくなります。

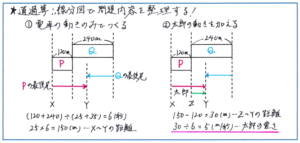
　通過算で図をかく際には、電車の動きはできるだけシンプルにしておくように心がけましょう。電車PとQがすれ違い始める時点の様子を表す際には、2つの電車の先頭が重なるように、すれ違い終わる時点については、2つの電車の最後尾の動きを電車ではなく、矢印で表せば1つの図の中におさめることができます。

　そこに太郎君が走る様子を図にかき込みますが、2つの電車の先頭どうしが重なる地点から太郎君が動きはじめ、最後尾どうしが重なる地点で動き終わるように、矢印をかき入れます。

　こうして上の右側の図のように問題内容が整理できれば、正解まではもうあと一歩です。電車PとQがすれ違いはじめてからすれ違い終わるまでにかかる時間は通過算の基本中の基本の式で、(120＋240)÷(25＋35)＝6（秒）と求められます。この6秒間で電車Pが進む距離は、25×6＝150（m）で、図より、太郎君が6秒間で進んだR～Q間の距離は、150mから電車Pの長さ120mを引いて求められます。よって、太郎君が自転車で進む速さは、(150－120)÷6＝5（m/秒）より、秒速5mと求められます。

　今回ご紹介した問題のように、一見複雑な問題でも、図を使って内容を整理できれば、図のどの部分を求めればよいかが視覚的に把握でき、多くの式を使うことなく解き進められます。特に速さの問題は視覚的に内容を把握することが必須となります。図をかく練習をしっかり重ねておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。