メールマガジン宝箱 Mail magazine

　今回の6年生4月度グノレブ実力確認テストは、春期講習の範囲に加えて、春期前に演習した、倍数算・年令算、さらには速さの問題まで含まれ、範囲が広いテストとなります。

　どの単元も入試頻出の重要単元であり、それぞれの単元について問題を見てすぐに解法を思い浮かべることができるようにしておく必要があります。特に比を使った解法を使いこなせるように、書き込みや書き出しをして問題内容を整理する作業が必須となります。

　テスト範囲が幅広く、問題内容を正しく整理して、比の解法を的確に使いこなす力が試される4月度グノレブ実力確認テストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの「50分で偏差値を5上げる算数予想問題」と組み合わせれば、グノレブ実力確認テスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　平面図形・立体図形：比を利用した解法を使いこなせていますか？】

　平面図形では、相似や面積比といった比を使った問題が様々なかたちで出されます。難度も高くなることが予想されますが、まずはテスト前半で出されるような基本的な内容を確実に得点することが必須です。

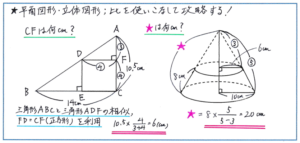
　例えば下のような直角三角形の中に正方形が含まれるような形についての問題。大きな直角三角形と、正方形のまわりにある2つの直角三角形がすべて相似の関係にあることはすぐに見て取れるでしょう。さらに、AC：BC＝10.5：14＝3：4であることから、AF：FD＝3：4となり、正方形の辺の長さがすべて等しいことから、FD＝CFとなることがわかります。そこで、AC＝10.5cmが比の(3＋4＝)7にあたるため、CFの長さが、10.5×4/(3＋4)＝6（cm）と求められます。

　こうした相似を利用する問題では、下の左の図のように、図の中にマル3、マル4といったかたちで比の値をかき込むことが正解に至るポイントとなります。視覚的に比の関係を把握できれば、解答方針をスムーズに立てられますので、ためらわずにかき込みをするように心がけましょう。

　また、右の図のような、円すい台の表面積を求める問題でも、相似の利用が必須となります。

　円すい台は大きな円すいから小さな円すいを除いた形ですので、体積や表面積を求める際には、大きな円すいを再現させたうえで解き進めることはすぐにわかるでしょう。

　円すい台の表面積は、上下の底面積（2つの円）と側面積で構成されますが、この側面積を求めるにあたって、大きな円すいの母線の長さが必要になります。ここで直角三角形の相似の関係から、大きな三角すいの母線の長さを、8×5/(5－3)＝20（cm）として求められれば、あとは側面積の公式、母線×底面の半径×3.14を使って、式を立てることができるのです。

　6年生になると、図形の問題のほとんどが相似や面積比といった比を利用して解く内容となります。相似を見つけ出す視点を鍛えることを目的として、普段の演習を地道に重ねるようにしましょう。

【第2位　グラフの問題：動きの変化とグラフの変化の関係を正確につかめていますか？】

　グラフの問題は、比例・反比例を表すものや、春期講習明けの「2量の関係」で学習する、タクシー料金に代表される段型のグラフなど多岐にわたりますが、特に注意すべきは「速さとグラフ」、「水深変化のグラフ」です。特に「速さとグラフ」は入試頻出であり、難度の高い問題が今回のグノレブで出されることが予想されます。

　その中でも、「2人の間の距離」を表したグラフの読み取りには複雑なものが多いため、注意が必要です。例えば、下のグラフでは、2人の出発時刻が異なる、1人が途中で休む、もう1人が途中で速さを変える、といった変化が3つも含まれます。

　こうしたグラフを読み取る際には、「グラフが折れる点で何が起きているのか」「グラフの傾きがどのように変化しているのか」といった基本に立ち返って、動きの変化をつかむことが必須となります。

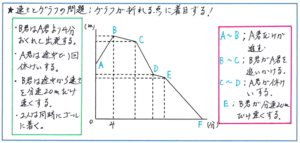
　2人の間の距離を表すグラフを読み取る際に、1人ずつのグラフをかくことで、距離の変化を理解する方法もありますが、グラフの作成に時間がかかるうえ、2人の間の距離のグラフとの関係が必ずしもスムーズにはできないことがあります。より短い時間で正確に変化の様子を読み取るために、グラフの中の変化を的確にとらえる練習を重ねておきましょう。

【第3位　速さの問題：問題内容に合わせた解法を的確に使いこなせていますか？】

　入試最頻出単元のひとつである「速さの問題」は、6年生になると難度が一気に増してきます。グノレブでも終盤に出されるような速さの問題は、問題文が長く複雑になるケースが多く、その内容を正確に整理できなければ、解答の道筋が見えてきません。問題文を落ち着いて正確に読み取り、そこからどの解法を使えばよいのか、といった思考の流れをスピーディーに進める必要があります。

　その際に必須となるのが、使いこなせる解法を多く持っておくことで、特に「平均の速さ」と「速さのつるかめ算」は使うケースが多くありますので、解法をいま一度確認しておきましょう。

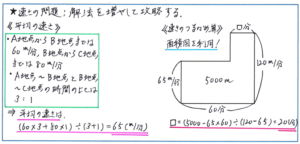
　平均の速さでは、行きにかかった時間と帰りにかかった時間、往復の合計距離、といった解答に必要な情報が具体的な数値で与えられているような基本パターンだけでなく、例えば「A地点からB地点までは分速60mで、B地点からC地点までは分速80mで進み、A地点からB地点までにかかった時間とB地点からC地点までにかかった時間の比が3：1であった場合のA地点からC地点までの平均の速さは分速何mか」といった比を使ったかたちで問題が構成されることもあります。

　そうした場合でも、(平均の速さ)＝(移動距離の合計)÷(移動時間の合計)の式にあてはめれば、(60×3＋80×1)÷(3＋1)＝65(m／分)として、平均の速さを求めることができます。比を数値化して基本公式にあてはめれば、スムーズに正解に行き着くことができるのです。

　速さのつるかめ算もまた、つるかめ算の基本公式が使えれば難なく正解を導き出すことができますが、ポイントはつるかめ算を使うケースかどうかの判断を、問題文を読んで正確に行うことにあります。

　例えば、先程の速さの平均の問題の続きで、「C地点からD地点までは分速120mで進んだところ、A地点からD地点まで合計で1時間かかりました。A地点からD地点までが5000mのとき、C地点からD地点まで進むのに何分かかりましたか」といった問題があるとします。

　A地点からC地点までの速さ（ここでは平均の速さ）、C地点からD地点までの速さ、A地点からD地点まで進む時間の合計、距離の合計が与えられていますので、ここで瞬時につるかめ算を使う、と判断ができるようにしておきたいところです。

　速さであろうと、つるかめ算の基本公式であることに変わりはなく、(5000－65×60)÷(120－65)＝20（分）と、式さえ立てられれば、答えを出すことは難しくありません。

　平均やつるかめ算といった解法をすぐに思い浮かべられるようにするために、間違った問題はもちろん、正解した問題でも必ず解法を確かめる習慣を身につけておきましょう。

【第4位　年齢算：人数が多いパターン、比を利用するパターンに対応できていますか？】

　年齢算の中でも、例えば「現在、太郎君は12才、父は42才です。父の年齢が太郎君の年齢の3倍になるのは何年後ですか」といった基本パターンであれば、差一定の考え方から、必要であれば線分図を利用して、(42－12)÷(3－1)＝15、15－12＝3より3年後という答えが大きな負担なく求めることができるでしょう。

　それが応用問題となると、人数が増えたり、比を利用するといったかたちで難度が大きくアップします。今回のグノレブ対策としては、難度が上がったパターンまで徹底的に習得しておきたいところです。

　例えば、「現在、父の年齢は36才、母の年齢は35才で、3人の子どもたちの年齢は、5才、3才、1才です。父母の年齢の和と3人の子どもたちの年齢の和の比が3：2になるのは、今から何年後ですか」といった問題では、どのように解き進めればよいでしょうか。

　年数がたっても1人と1人を比べた際に年齢の差が変わらない状況は同じですが、この問題のように父母（2人）と子どもたち（3人）と比べる対象の人数が異なると、単純な差一定の考え方で進めることができなくなります。

　そこで、これもまた年齢算の定型の解法ですが、求める答えを「マル1年後」として、式での処理を進めます。

　父の年齢は（36＋マル1）才、母の年齢が(35＋マル1)才、3人の子どもたちの年齢はそれぞれ、(5＋マル1)才、(3＋マル1)才、(1＋マル1)才と表すことができます。ここで「父母の年齢の和と3人の子どもたちの年齢の和の比が3：2になる」という部分から、(36＋マル1＋35＋マル1)：(5＋マル1＋3＋マル1＋1＋マル1)＝3：2としてから式を整理して、(71＋マル2)：(9＋マル3)＝3：2とします。

　この比の式さえできてしまえば、テキスト『式の処理と倍数算・年齢算』の1ページ目に掲載されている問題の通り、式の内積（内側の積）と外積（外側の積）が等しいことから、(9＋マル3)×3＝ (71＋マル2)×2より、27＋マル9＝142×マル4より、マル1＝(142－27)÷(9－4)＝23（年後）と正解を導くことができます。

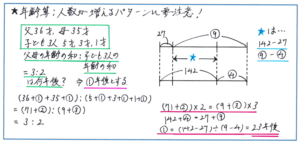
　最後の、27＋マル9＝142×マル4の式について、グノーブルではこのタイプの比の式の処理の練習を徹底的に行ってきましたので、スムーズに解き進められると思われますが、解き方に迷った際には、上の右のような線分図で整理してもよいでしょう。

　今回の範囲が広いグノレブにおいて、年齢算の問題では何とか正解を確保したいところです。一連の解き方の流れの中で、理解が曖昧なところがないように、しっかりチェックしておきましょう。

【第5位　場合の数：書き出しと計算の組み合わせを的確に使いこなせていますか？】

　場合の数からも今回のグノレブでの出題が予想される問題が多岐にわたってあります。問題によっては書き出しのみで正解できるものや、計算ですぐに正解を得られるものもありますが、6年生になると、書き出しと計算の両方を求めるタイプの出題が増えてきます。そういった問題に対して、どこまで書き出して、どこから計算に切り替えるか、落ち着いて迅速に判断する力が求められるのです。

　例えば、「1から5のカードが2枚ずつあります。この中から3枚取り出して並べるとき、3枚のカードの数字の和が8になるような並べ方は何通りありますか」といった問題。

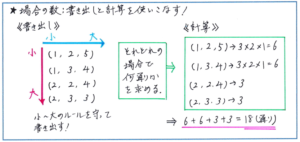
　上の通り、まずは3つの数を足して8になる組み合わせを書き出すのですが、ここで書き出しにもれや重複がないようにするために、小さな数から選ぶ鉄則を守るようにしましょう。

　そこで書き出した4通りの組み合わせについて、それぞれの場合のカードの並べ方を求めることで、その和を答えとすることができます。

　書き出しにもれや重複がないか、式の立て方に間違いがないかといった点について、しっかりチェックしておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。