メールマガジン宝箱 Mail magazine

　今回の組分けテストでは、「速さ」での運転間隔や往復グラフの問題、「平面図形」での相似、面積比、「場合の数」での最短経路など、自分で図をかく、または図やグラフにかき込みをするといった手作業を多く求める単元が出題範囲となります。

　ただ闇雲に手作業を進めても、時間がかかり正答率も上がらないといった事態が起こりがちです。しっかり解法の意味を理解したうえで練習を重ねて、正確で効率的な手作業を求める第2回組分けテストで、一気にクラスアップを実現したいところです。　　

　そこで、第2回組分けテストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの「50分で偏差値を5上げる算数予想問題」と組み合わせれば、組分けテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　速さのグラフ：往復運動を表すグラフから解答に必要な情報を得られていますか？】

　速さの問題の中でもグラフを使って解く問題は、どれだけ問題文から得られた情報をグラフの中にかき込み、また解答に必要な情報をそこからピックアップできるかで、解答速度と正確さに大きな違いが生まれます。特に動きが複雑な問題では、グラフを通して解法のイメージを明確にする必要があります。

　その典型的な例が「往復運動」を扱う問題です。往復運動を表すグラフから、いかに解答に必要な情報、特に「比」に関する情報をスピーディーに入手するかが正解に至るポイントとなります。

　例えば、「AさんがP地点を、BさんがQ地点を同時に出発して、それぞれ一定の速さでPQ間を1往復しました。グラフは2人の進んだ様子を表したものです。グラフのアにあてはまる数を求めなさい」といった問題では、どのようにグラフを読み解けばよいでしょうか。

　解答の方針としては、アはBさんが1往復してQ地点にもどる時間となります。グラフよりAさんが1往復してP地点にもどる時間が60分と与えられていますので、「2人が同じ道のりを進む時間の比」がわかれば一気に解答に近づきます。

　ここで注意すべきは2人がどちらも一定の速さで動いていることです。流水算や速さが変化するような問題ではありませんので、2人ともに「行きと帰りにかかる時間が同じ」になります。それによって、AさんがP地点からQ地点まで進むのにかかる時間が、60÷2＝30（分）とわかり、Q地点と2人がすれ違う地点の間の道のりを、Aさんは、30－12＝18（分）、Bさんは12分で進んだことがわかり、「同じ道のりを進むのにかかる時間の比」が、18：12＝3：2となることから、Bさんが1往復する時間、すなわちアの時間を、60×2/3＝40（分）と求めることができます。

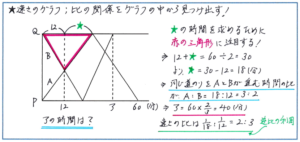
　今回の問題では、時間の比をそのまま使うことで解答に行き着くことができましたが、これが、AさんとBさんの速さの比を求めなさい、といった問題になっても、「同じ道のりを進む場合の速さの比は、かかる時間の逆比」の考え方を使えば、1/18：1/12＝2：3と求めることができます。

　ポイントはグラフの中の三角形を見つけ出して、同じ道のり、同じ時間の関係を見つけ出すことにあります。これは往復の問題に限らず、2人の動きを表したグラフを使った問題では必須の解法となります。問題演習を重ねて、グラフを読み解く目を鍛えておきましょう。

【第2位　平面図形：面積比と辺の長さの比の関係をすぐに見つけ出せていますか？】

　平面図形の問題では、6年生になって比を使うケースが非常に多くなってきます。そうした問題では、相似や面積比（同じ高さを持つ図形の面積比が辺の比になる）を利用しますが、注意しておきたいのが、図形の向きに関わらず、比の関係を正確につかむことです。

　相似でも面積比でも、テキストの基本問題に掲載されているような典型パターンには対応できても、図形の向きが変わるだけで対応しづらくなってしまうことがあります。6年生の組分けテストになると、典型的な基本パターンは出されるとしても大問2までで、中盤以降の応用問題では「視点の切り替え」が必要となります。

　例えば下の三角形で、「AD：BD＝4：3で、三角形ACDの面積が32平方cm、三角形BDEの面積が9平方cmのとき、BE：CEを最も簡単な整数の比で答えなさい」といった問題。AD：BD＝4：3が与えられていることから、三角形ABCについて辺ABを底辺として考えると、三角形ACDと三角形BCDは高さが共通となり、三角形ACDの面積と三角形BCDの面積の比は、AD：BDと等しく、4：3になります。これより、三角形BCDの面積が、32×3/4＝24平方cmとなることがわかります。

　ここで、三角形BDEと三角形CDEは高さが共通となることから、BE：CEは三角形BDEの面積と三角形CDEの面積の比と等しく、9：(24－9)＝3：5と求めることができます。

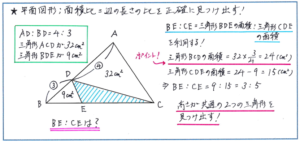
　最初の三角形ACDと三角形BCDの関係をつかむうえで底辺が水平ではなく、斜めに向きが変わりますが、こうした問題でもテスト用紙を回したりせずにスムーズに比を利用できるように、普段からテキストの応用問題を多く解いて、図形を見る視点を鍛えましょう。

【第3位　平面図形：正六角形の中の面積比を正確に覚えられていますか？】

　今回の組分けテストでは、平面図形の中の「正六角形」を素材とした問題も、要注意単元となります。正六角形を分割してできる三角形、四角形と、もとの正六角形の面積比を利用して解かせる問題が多く出されますので、正六角形の面積比の基本パターンを徹底的に覚え込んでおきましょう。

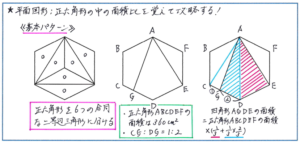
　基本パターンのひとつは正六角形を3本の対角線で6つの正三角形に分ける（ピザやケーキを6等分するように）かたちですが、こちらはイメージもしやすく、面積比を確実に覚えられるでしょう。

　注意すべきは下の左の図のように、正六角形を6つの二等辺三角形に分けるかたちです。中央の二等辺三角形3つでできる正三角形の面積が正六角形の面積の1/2になることもしっかりおさえておきましょう。

　そのうえで、例えば下の中央の図で「正六角形ABCDEFの面積が360平方cmで、点Gが辺CD上にあって、CG：DG＝1：2のとき、四角形AGDEの面積は何平方cmですか」といった問題を考えてみましょう。

　この問題では、三角形AEFの面積が正六角形ABCDEFの面積の1/6になることは基本となりますが、四角形ABCGの面積はすぐに求められず、「正六角形の面積から求める四角形の面積以外を引く」という解法では進めづらくなります。

　そこで補助線の引き方が重要になります。まずは、AとDを結んで三角形AGDと三角形ADEに分けて考えます。三角形ADEの面積は、正六角形ABCDEFの1/2の面積である台形ADEFから、1/6の面積である三角形AEFを引くことで求められますので、正六角形ABCDEFの面積の(1/2－1/6＝)1/3となります（この1/3も覚えておくようにしましょう）。

　次に三角形AGDの面積ですが、CG：DG＝1：2であることを利用するために、AとCを結んで、三角形ADEと合同で、正六角形ABCDEFの面積の1/6である三角形ACDをつくり、三角形ACDと三角形AGDの底辺比が、(1＋2)：2＝3：2であることから、三角形AGDの面積が正六角形ABCDEFの面積の、1/3×2/3＝2/9と求めることができます。

　以上より、四角形AGDEの面積は、正六角形ABCDEFの面積の、(1/3＋2/9＝)5/9となり、360×5/9＝200平方cmと求めることができるのです。

　組分けテストで正六角形の問題が出される場合には、何本もの直線が正六角形の中に引かれるような複雑な難問となる可能性が高いですが、今回の解法のように、基本パターンをしっかりとおさえて、面積比が活かせるような補助線の引き方を強く意識すれば、正解への道筋が開けてきます。基本パターンと比の使い方、それらを活かすための補助線の引き方を習得できるように、練習を重ねましょう。

【第4位　運転間隔の問題：運転間隔にあたる部分を図を使って正しく表現できていますか？】

　速さの問題の新出テーマの中で、「運転間隔」の問題は、動きをイメージすることが難しく、問題内容を整理するための図の作成が難しい単元です。ただ、作図の方法、運転間隔を図に盛り込む方法を習得できれば、式は立てやすいため、複雑な通過算の問題よりも解きやすくなります。

　例えば、「一定の速さで線路ぞいを走る自転車が、上り電車に18分おきに追いこされ、下り電車と9分おきにすれちがいました。自転車と電車の速さの比を求めなさい。ただし、上り電車と下り電車の運転間隔は同じで、上り電車と下り電車の速さは同じです。また、電車や自転車の長さは考えません。」といった問題。

　自転車と電車の速さの比を求めるにあたって、与えられているのが、18分と9分という時間であることから、逆比を利用することは思いつきますが、その場合は「同じ道のり」をどのように設定するが課題となります。

　この問題で同じ道のりとして使えるのは、問題文にある「上り電車と下り電車の運転間隔は同じ」の部分となります。そこで、上りと下りの2つのケースにおいて、同じ道のりとなる運転間隔をどのように図に盛り込むかを考えると、下のようになります。

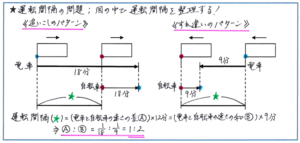
　追いこされる場合には電車の最後尾に印を、すれちがう場合には電車の先頭に印をつけておく（最後尾と先頭は逆でも構いません）と、どの部分に18分かかり、9分かかったのかをイメージしやすくなります。

　あとは、2つの図に共通して、電車間の距離が運転間隔に当たると理解できますので、その運転間隔が、(電車と自転車の速さの差)×18分と、(電車と自転車の速さの和)×9分という2つの式で表せることから、(電車と自転車の速さの差)：(電車と自転車の速さの和)＝1/18：1/9＝2：1とすることができます。

　最後は、比の和差算の考え方（消去算の考え方でも解くことができます）で、(電車の速さ)：(自転車の速さ)＝(2＋1)÷2：(2－1)÷2＝1.5：0.5＝3：1と求めることができます。

　『予習シリーズ算数6年上』の65ページの図では、バスの長さは表されていません。問題でも「電車や自転車の長さは考えません」と書かれていますので、あえて長さを表さなくてもよいのですが、通過算の考え方を習得した皆さんからすると、電車に追いこされる、電車とすれちがう、といったケースは、簡単に電車の図を入れた方がイメージを持ちやすいかもしれません。

　速さの問題をパターンで解く際には機械的に数を当てはめるのではなく、なぜその式が成り立つのかを考える意識をしっかり持つようにしましょう。それが6年生算数の応用問題を解く際の重要な前提条件となります。

【第5位　場合の数：難問に対応できるように、複数の解法を身につけておきましょう！】

　場合の数の問題では、同じ問題内容に対して複数の解き方を持っておくことが重要になります。6年生になって問題の難度が上がった場合でも、書き出しや表をつくるなどを通して地道に解答を求める方法と、計算のみで解き進める方法の両方を使い分けることができれば、正解のチャンスも大きく増大します。

　例えば、「道順」の問題は、マス目で示された道の、端から端まで最短経路で行く方法を求めるタイプの問題ですが、マス目の端に数字を書き込んで、その和を書き連ねて行く解法がまずは浮かんでくるでしょう。

　この解法は、計算を機械的に、スピード感をもって進められるメリットがありますので、答えの数が小さいケースではとても有効です。まずはこの書き込みの方法を徹底的に覚えて、正しく使えるようにしておきましょう。

　ただし、マス目の数が多くなり、最終的な答えが3ケタ以上の数になってしまうような場合、書き込みの解法では、たし算の過程でミスが起きやすくなってしまいます。このパターンの問題は、途中で1つでもたし算のミスをしてしまうと、そこから連動して間違いが起きてしまいますので、細かな計算ミスは何としても防がなくてはなりません。

　かといって、計算の工夫ができるタイプの問題ではありませんので、この解法を使う場合は、ただ正確に解くことに尽きてしまいます。

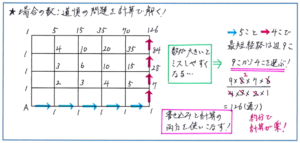
　そこで、別の解法を考えてみましょう。上の図のようなマス目の場合、A地点からB地点まで最短経路で行くには、マス目の辺を横に5個、たてに4個、合計して9個の辺を進めばよいことになります。

　ここから、9個の辺のうち4個をたての辺にする、という点で、「9個の辺から4個の辺を選ぶ選び方」と考えられるのです。こうなれば、計算は、(9×8×7×6)/(4×3×2×1)の式で進められます。この分数式では約分ができる数の組み合わせがありますので、結果、9×7×2＝126（通り）と、いたって簡単な計算で正解まで行き着けるのです。

　まずはマス目に書き込むといった基本パターンをしっかり覚え込み、計算ミスが起きやすいケースであると感じられた場合には、別の解法（今回であれば選び方の方法）を使う、という判断ができるように、解法を少しでも多く備えておくようにしましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。