メールマガジン宝箱 Mail magazine

　今回は「平面図形と比」の中で、面積比の問題に要注意です。相似という大事な単元を優先するあまり、高さ一定などの面積比の復習が手薄になってしまわないように気をつけてください。また、仕事算、流水算は図を使いこなせるかどうかが勝負の分かれ目になります。ランキングでご紹介する5つのポイントをしっかりおさえて、偏差値アップ、クラスアップを実現してください。応援しています！
　さらに、このメルマガは明日公開の予想問題と連動しています。これから紹介するランキングと予想問題を照らし合わせれば今度のマンスリーの勝者となれます！頑張ってください！
予想問題はこちらのページで無料公開します！

【第5位　縮尺の問題：面積の単位は確実に覚えられていますか？】

　縮尺の問題では、計算を分数型で進めること、単位換算に注意することがポイントです。例えば、

といった問題。まず式の立て方ですが、
360×100×100×100÷4000÷4000＝22.5（平方cm）
としてもよいのですが、分数のかたちにすると、0（ゼロ）をスムーズに消せるメリットがあります。
また、面積の単位（平方cm、平方m、a、ha、平方km）の換算が曖昧になっていないか、必ずチェックしておきましょう。せっかく計算ができても単位換算で間違えてしまっては、あまりにもったいないです。

【第4位　面積比①：同じ面積の部分に数値を記入して、等積関係を見やすくしましょう！】

　面積比で、三角形を同じ面積に分けるタイプの問題があります。例えば、

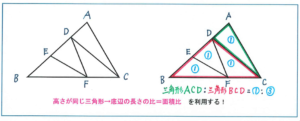
このタイプの問題は、高さが同じ三角形では、底辺の長さの比が面積比となることを利用して解き進めます。そこで、面積の比がわかりやすくなるように、同じ面積にあたる部分に①などの記号を記入していきます。右の図で、三角形ＡＣＤと三角形ＢＣＤは高さが共通で、面積の比が①：③より１：３となるので、ＡＤ：ＢＤ＝１：３が求められます。ここでＢＤの長さが4×3=12(cm)となります。
同じように三角形ＤＥＦと三角形ＢＥＦを見ると、面積は①：①＝１：１より、ＤＥ：ＢＥ＝１：１となるため、ＤＥの長さは、12÷2＝6(cm)と求められるのです。
慣れてくれば記号の記入は不要になりますが、少しでも面積比の関係を見やすくするためにも、ぜひ記号の記入を実践してみて下さい。
　

【第3位　面積比②：辺の長さの比をかけ合わせるパターンは補助線なしで！】

　面積比で三角形を辺どうしを結ぶ線で分けるタイプの問題があります。例えば、

といった問題です。

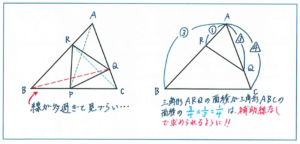
　解答の方針は、三角形ＡＢＣから三角形ＡＲＱ、三角形ＢＰＲ、三角形ＣＰＱの面積を引いて、三角形ＰＱＲの大きさを比で表すことになります。
　ここで、三角形ＡＲＱが三角形ＡＢＣの何分のいくつかを求める際に、ＢとＱを補助線で結んで考える方法があります。三角形ＡＢＱが三角形ＡＢＣの3/4、三角形ＡＲＱが三角形ＡＢＱの1/3より、三角形ＡＲＱは三角形ＡＢＣの3/4×1/3＝1/4、と求める流れですが、できればこの式は補助線なしで求められるようにしておきたいところです。求める三角形の面積比がひとつであればまだしも、この問題のように3つの三角形で面積比を求めるとなると、左の図のように、線が渋滞を起こしてしまい、どの部分の面積を求めるのかが、わからなくなってしまいます。
　まずは補助線で面積比の求め方の流れを理解したうえで、できるだけ早い段階で、補助線なしで面積比を求められることを目指しましょう。

【第2位　仕事算：途中で1人が休むパターンは面積図で攻略できる！】

　仕事算の中で難度が高いタイプのひとつが、次のようなタイプの問題です。

　このように、途中で全体の仕事量が減るようなタイプの問題は、状況を具体的にイメージがしづらいこともあり、苦手とされるケースが多いです。こうした問題は慣れるまでは、図で内容を整理すると式が立てやすくなります。下のような図になります。

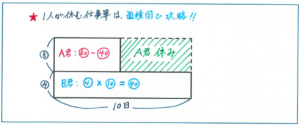
　上記のように仕事量を面積で表すことで、途中で1人が休む、といった状況も視覚的に把握できるメリットがあります。
　あとは、全体の仕事量を1とするよりも、12と15の最小公倍数である60とおくことで、分数計算をする必要がなくなり、計算ミスを起きづらくすることができます。
　マル60－マル4×10＝マル20…Ａ君だけが行った仕事量
　マル20÷マル5＝4（日）…Ａ君が仕事を行った日数
　10－4＝6（日）として正解に行き着くことができます。
　慣れてくれば面積図をかく必要はなくなりますが、1人が休む、といった状況をイメージするために、ぜひ面積図をかく解法を試してみてください。　

【第1位　流水算：上り下りを瞬時に把握できるような図のかき方はできていますか？】

　流水算は、静水時の速さ、上り・下りの速さ、流れの速さの関係を線分図に表すことができれば、決して難しい問題ではありません。例えば「下りは上りの時よりも川の流れの速さが3倍になった」といった頻出のパターンも、線分図で流れの速さの部分を3倍に延ばせば、式をスムーズに立てることができます。
　むしろその前段階として、上りと下りの関係を正確に瞬時に把握できているかどうかをチェックしておく必要があります。特に問題文が長くなりがちな流水算ですので、上りなのか下りなのかという基本情報を把握できなくなってしまうことが起こり得ます。
そこで、下の左の図のように傾斜をつけた線分図をかいておくと、どちらの船が上るのかで迷うことがなくなります。すでに実践されている方々も多いかと思いますが、ちょっとした工夫で失点を防げる方法ですので、ぜひ試してみて下さい。

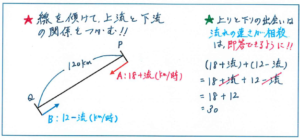
もう1点、流水算と旅人算が合わさった問題。

　ここでＡ船とＢ船が1時間ごとに、18＋12＝30(㎞)距離を縮めることは、問題を見た瞬間に答えられるようにしておきましょう。Ａ船、Ｂ船の速さの和の式をかけば、流れの速さが相殺されることは明らかです。ここはテストでも得点源にしたいところですので、テスト前にしっかり確認をしておきましょう。　
　問題の答えは、120÷(18＋12)＝4（時間）となります。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。