メールマガジン宝箱 Mail magazine

　速さとケアレスミスは双子のような関係です。ズバリ！今回のテストで偏差値を大幅にアップさせるポイントはケアレスミスを防ぐことです！毎年、理解度が不足しての間違いではなく、問題内容を取り違えてしまい実力通りの偏差値が出ないという事態が起こっています。いかにしてケアレスミスを防ぐか、そして速さの問題での得点力をいかにアップさせるかを中心にポイントを説明していきます。ぜひ、偏差値アップ、クラスアップを実現してください。応援しています！
　さらに、このメルマガは明日公開の予想問題と連動しています。これから紹介する4つのポイントと予想問題を合わせれば偏差値がジャンプアップします！
予想問題はこちらのページで無料公開します！

【直前チェックポイント１：ミスを防ぐ問題の読み方ができていますか？】

　例えば、次のような問題。

　単純な向かい合いの旅人算ですので、式を立てることは難しくないでしょう。ポイントは問題の答えです。式で出た数値が問題の答えとして正しいかどうかに十分に注意しなくてはなりません。
　80×4＝320（m）
…花子さんが出発する時点で太郎君が進んだ道のり
　2000－320＝1680（m）
…花子さんが出発する時点での2人の間の道のり
　1680÷(80＋60)＝12（分後）
…花子さんが出発してから2人が出会うまでの時間
　ここで答えを12分後としてしまうミスがとても多く見られます。問題で聞かれているのは「太郎君が出発してから」の時間ですので、上記の答え12分後に4分をプラスしなければなりません。よって正解は12＋4＝16（分後）です。
　せっかく計算が正しくできていても最後のところで別の内容を答えてしまうミス。今回のテストは旅人算、時計算、通過算に加え、点の移動も範囲になります。問題文が長く、条件が複雑な問題が多いことで、解答の時間がなくなり焦ってしまった結果、普段の演習では起こさないようなミスが多発してしまうのです。
　そうしたミス防止の対策として、問題を読む際に答えになる部分、今回の問題であれば「太郎君が出発してから」のところに線を引くなど印をつけて、何を求めるのかを視覚的にも目立たせるとよいでしょう。大事なところに線を引くのは国語だけのことではないのです。たかがミスと思っていても、それが積み重なると大きな失点につながります。逆に言えば、ミスを防ぐことで得点が上がり、偏差値がアップすることになります。どうかミス防止の具体的な対策を大事にしてください。

【直前チェックポイント２：往復の旅人算で道のりを何倍するかが曖昧になっていませんか？】

　旅人算の中でも難度が高く、苦手にしているお子様が多いのが往復のパターンです。2者が向かい合って進むだけの状況であればまだイメージができるものの、往復となるとなかなか頭の中で想像するに限界があります。そうしたイメージのしづらさが、苦手意識につながっているのでしょう。
　往復の旅人算で特に問題になるケースが多いのが、「2人が2回目に出会ったのは」のパターンです。
　問題によって時間を求めるケース、道のりを求めるケースと分かれますが、ポイントになるのは「2人がスタートしてから2回目に出会うまでに進んだ道のりは、基本の道のりの3倍」という点です。ここで言う「基本の道のり」とは、例えばＡ君とＢ君が100m離れた地点から向かい合って進む場合であれば100m、のように最初の段階で離れた道のりのことを示します。
　ここで2回目だから2倍、といったミスは何としても避けたいところです。
　こうしたミスを防止するには、線分図をかいて状況を整理することが効果的です。テストでは色ペンなどは使えませんが、自宅学習で理解を固めるには、下の図のように色分けをするのもよいでしょう。　

　1回目の出会いから2回目の出会いまでに2本分の道のりがプラスされましたので、例えば3回目に出会う場合には、その道のりは3＋2＝5（本分）、つまり基本の道のりの5倍となります。このパターンは問題を見てすぐに、できればテスト会場では線分図なしで何倍かがわかれば、そのテストで圧倒的な優位に立てます。そのためにもまずは図をかく練習を重ねて、慣れを身に付けましょう。

【直前チェックポイント３：時計算ではスタートの時刻も図にしておきましょう！】

　時計算の問題を解く際にミスを防ぐためには、スタートの時刻を時計の図で表しておくことが効果的です。例えば「4時と5時の間で、長針と短針が重なり合うのは、4時何分ですか。」といった問題。解答の進め方は、スタートの段階での角度の差÷(6－0.5)という式を立てることで方針は固まっているので対応しやすいのですが、その最初の段階の角度の差を間違えてしまっていては、すべてが崩れてしまいます。スタートの段階さえ間違わなければ正解できる可能性（分数計算に十文注意したうえで）が高い問題ですので、まずは時計の図で、スタートの段階を正しく認識するようにしましょう。そうすることで、時計算を大きな得点源にできます！

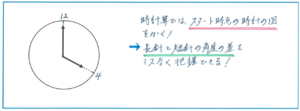
【直前チェックポイント４：通過算では道のりの見方でミスをしないように図を活用しましょう！】

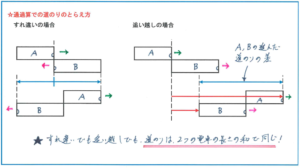
　通過算では道のりを正確に把握することが偏差値アップのポイントになります。電車がトンネルや橋を通過する問題であれば道のりは正しくとらえやすいのですが、注意すべきは電車どうしがすれ違ったり、追い越したりするタイプの問題です。こうした問題では、速さは「すれ違い→速さの和」「追い越し→速さの差」と違いがありますが、道のりについてはどちらも同じく「2つの電車の長さの和」になります。
　追い越しだから電車の長さも差にする、といったミスがないように、慣れるまでは下のような図で整理しておくとよいでしょう。

　入試問題において通過算や時計算は、特に上位校で出題された場合に、複雑な構成になることが多い単元です。それだけにミスも起きやすい単元と言えます。5年生のうちに基本パターンをしっかり身に付けておくことが、ミス防止の第一歩になります。慣れるまでは図で内容を整理して、ミスが起きにくい状況をつくるようにしましょう！

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。